جداول الصواب في المنطق الرياضي: كيف تبني أي جدول خطوة بخطوة؟

جداول الصواب أداة منهجية في المنطق الرياضي تُستخدم لتحديد القيمة المنطقية لأي عبارة مركبة. تعرض هذه الجداول جميع الاحتمالات الممكنة للمتغيرات المنطقية ونتائجها النهائية. تُعَدُّ جداول الحقيقة الركيزة الأساسية لتصميم الدوائر الرقمية وبرمجة الحاسوب. يعتمد عدد صفوف الجدول على عدد المتغيرات وفق المعادلة 2^n، حيث n يمثل عدد المتغيرات.

هل تساءلت يوماً كيف يتخذ حاسوبك قراراً في جزء من الثانية؟ أو كيف تعرف أن حجة صديقك في النقاش واهية رغم أنها تبدو منطقية؟ لقد واجهت شخصياً هذا الإرباك حين درست المنطق لأول مرة. كانت العبارات الشرطية تحديداً تُربكني؛ إذ لم أفهم لماذا تكون “إذا 2+2=5، فالقمر مصنوع من جبن” عبارة صحيحة منطقياً! لكن جداول الصواب غيّرت كل شيء. في هذا المقال، ستجد الأدوات الكاملة لفهم وبناء أي جدول صواب مهما بلغ تعقيده. ستتحول من شخص يحفظ القواعد إلى شخص يفهم لماذا تعمل هذه القواعد من الأساس.

ما هو جدول الصواب ولماذا نحتاجه؟

تخيل أنك محقق جنائي تستمع لشهادتين متناقضتين. الشاهد الأول يقول: “إذا كان المتهم في المنزل، فقد سمعت صوت الباب.” الشاهد الثاني يؤكد: “المتهم كان في المنزل، لكنني لم أسمع أي صوت.” كيف تحدد من يكذب؟ هنا يأتي دور جداول الصواب.

جدول الصواب (Truth Table) هو ترتيب منظم يعرض كل الاحتمالات الممكنة لقيم المتغيرات المنطقية ونتيجة العبارة المركبة في كل حالة. فكر فيه كخريطة شاملة تكشف سلوك أي عبارة منطقية تحت جميع الظروف الممكنة. بالمقابل، لا يمكنك الاعتماد على الحدس وحده لتحليل عبارات معقدة تتضمن ثلاثة متغيرات أو أكثر.

لماذا ندرس هذه الجداول؟ الإجابة متشعبة. أولاً، تُشكّل جداول الحقيقة الأساس الذي تقوم عليه الرياضيات المجردة. ثانياً، كل جملة شرطية (if statement) في أي برنامج حاسوبي تعتمد على المبادئ ذاتها. ثالثاً، المهندسون الإلكترونيون يحوّلون هذه الجداول إلى بوابات منطقية (Logic Gates) تُشكّل قلب كل معالج في العالم. وعليه فإن فهم جداول الصواب ليس ترفاً أكاديمياً، بل مهارة عملية تتقاطع مع عشرات التخصصات.

اقرأ أيضاً:

• ما هو المنطق الصوري: وكيف يُشكّل أساس التفكير السليم؟
• ما هو المنطق الرمزي: وكيف تُترجم الأفكار إلى لغة الرموز الدقيقة؟

ما هي العبارة المنطقية وكيف تختلف عن الجملة العادية؟

ليست كل جملة نقولها عبارة منطقية. انظر إلى الفرق الجوهري: الجملة “أغلق الباب!” ليست عبارة منطقية لأنها أمر. الجملة “هل السماء زرقاء؟” ليست عبارة منطقية لأنها سؤال. بينما الجملة “السماء زرقاء” عبارة منطقية لأنها تقرير يمكن الحكم عليه بالصواب أو الخطأ.

العبارة المنطقية (Proposition) جملة تقريرية تحتمل قيمة واحدة فقط: إما صائبة (True) وإما خاطئة (False). لا وسط بينهما. هذا ما يُسمى “مبدأ الثالث المرفوع” (Law of Excluded Middle). من ناحية أخرى، العبارات الغامضة مثل “الطقس جميل اليوم” تُعَدُّ إشكالية في المنطق الصوري؛ إذ تعتمد على تفسير شخصي.

نرمز للعبارات المنطقية البسيطة بحروف صغيرة: p, q, r, s. مثلاً:

• p: “القاهرة عاصمة مصر” (صائبة)
• q: “3 > 5” (خاطئة)

هذه العبارات البسيطة نسميها “عبارات ذرية” (Atomic Propositions). عندما نربطها بأدوات الربط المنطقي، نحصل على “عبارات جزيئية” أو مركبة (Compound Propositions).

كيف نقرأ قيم الصواب والخطأ؟

في الأدبيات الأكاديمية العربية والعالمية، تجد رموزاً مختلفة لقيم الصدق والكذب. فهم هذه الرموز ضروري لقراءة أي مرجع:

في الرياضيات والفلسفة:

• T (True) للصواب
• F (False) للخطأ
• أحياناً تجد: ⊤ للصواب و ⊥ للخطأ

في علوم الحاسوب والهندسة الكهربائية:

• 1 للصواب (وجود تيار كهربائي)
• 0 للخطأ (غياب التيار)

الترميز الثنائي (1/0) ليس مجرد اختصار؛ إنه يعكس الواقع الفيزيائي للدوائر الإلكترونية. كل ترانزستور في معالج هاتفك يعمل كمفتاح: إما مفتوح (0) وإما مغلق (1). وبالتالي، جداول الصواب تترجم مباشرة إلى تصميم العتاد الصلب (Hardware).

كيف نحسب عدد صفوف الجدول قبل بنائه؟

سؤال يطرحه كل مبتدئ: كم صفاً سيحتوي جدولي؟ الإجابة بسيطة رياضياً. إذا كان لديك n من المتغيرات، فعدد الصفوف = 2^n.

لماذا؟ لأن كل متغير له احتمالان فقط (T أو F). ومع كل متغير جديد، تتضاعف الاحتمالات:

• متغير واحد (p): 2^1 = 2 صفان
• متغيران (p, q): 2^2 = 4 صفوف
• ثلاثة متغيرات (p, q, r): 2^3 = 8 صفوف
• أربعة متغيرات: 2^4 = 16 صفاً

هذا النمو الأسي يوضح لماذا تصبح الجداول ضخمة بسرعة. جدول بعشرة متغيرات يحتوي 1024 صفاً! لهذا السبب، يلجأ المهندسون إلى تقنيات الاختزال مثل خرائط كارنو (Karnaugh Maps) للتعامل مع العبارات المعقدة.

اقرأ أيضاً:

• الكمبيوتر: كيف غيّر هذا الاختراع العظيم مسار الحضارة البشرية؟

ما هي أدوات الربط المنطقي الخمس الأساسية؟

أدوات الربط المنطقي (Logical Connectives) هي الغراء الذي يربط العبارات البسيطة لتكوين عبارات مركبة. سأشرح كل أداة بجدول صواب ومثال حياتي.

النفي (Negation - NOT)

أبسط العمليات المنطقية. النفي يقلب قيمة العبارة: الصائب يصبح خاطئاً، والخاطئ يصبح صائباً. نرمز له بـ ¬p أو ~p أو NOT p.

مثال حياتي: إذا كانت p تعني "الباب مفتوح"، فإن ¬p تعني "الباب ليس مفتوحاً" (أي مغلق). في البرمجة، تستخدم علامة التعجب (!) للنفي: !isOpen تعني "ليس مفتوحاً".

الوصل (Conjunction - AND)

عملية "التشدد" المنطقي. العبارة المركبة صائبة فقط إذا كان كلا الطرفين صائباً. نرمز له بـ p ∧ q أو p AND q.

مثال حياتي: "سأذهب للنزهة إذا كان الطقس جميلاً وأنهيت عملي." يجب تحقق الشرطين معاً. إذا كان الطقس جميلاً لكنك لم تُنهِ عملك، لن تذهب. هذا منطق AND: لا تسامح، كل الشروط أو لا شيء.

الفصل (Disjunction - OR)

على النقيض من ذلك، الفصل "متسامح". يكفي أن يكون أحد الطرفين صائباً لتصبح العبارة المركبة صائبة. نرمز له بـ p ∨ q.

انتبه للفخ! الفصل المنطقي (OR) "شامل" (Inclusive). يعني: واحد على الأقل أو كلاهما. لكن في اللغة اليومية، نستخدم "أو" غالباً بمعنى "حصري" (Exclusive OR - XOR): إما هذا وإما ذاك، وليس كلاهما.

مثال: "هل تريد شاياً أو قهوة؟" في اللغة اليومية، تتوقع إجابة واحدة. لكن في المنطق الرياضي، الجواب "كلاهما" مقبول!

العبارة الشرطية (Implication - If...Then)

هنا يبدأ الإرباك الحقيقي لمعظم الطلاب. الشرط (p → q) يُقرأ: "إذا p، فإن q". المفاجأة أن العبارة الشرطية خاطئة في حالة واحدة فقط: حين تكون المقدمة صائبة والنتيجة خاطئة.

لماذا تكون "مقدمة خاطئة → أي نتيجة" صائبة؟ لنفهم بمثال.

مثال الوعد الانتخابي: سياسي يعد: "إذا فزت بالانتخابات، سأبني مستشفى." متى يكون كاذباً؟ فقط إذا فاز ولم يَبنِ المستشفى. لكن إذا خسر، لا يمكننا اتهامه بالكذب سواء بنى المستشفى أم لا. الوعد لم يُفعَّل أصلاً!

هذا التفسير يُسمى "الشرطية المادية" (Material Conditional). قد يبدو غريباً للوهلة الأولى، لكنه يحافظ على اتساق المنظومة المنطقية بأكملها.

الشرط الثنائي (Biconditional - If and Only If)

التكافؤ التام. العبارة (p ↔ q) صائبة حين يتفق الطرفان في القيمة: كلاهما صائب أو كلاهما خاطئ.

مثال: "ستنجح في الامتحان إذا وفقط إذا درست جيداً." هذا يعني: النجاح والدراسة مرتبطان تماماً. لا يمكن أن تنجح دون دراسة، ولا أن تدرس دون نجاح (نظرياً!).

اقرأ أيضاً:

• الاستدلال: المفهوم، الأنواع، ودوره في المعرفة
• الاستنتاج (Deduction): الانتقال من العام إلى الخاص

كيف تبني جدول صواب لأي عبارة معقدة؟

هذا القسم هو قلب المقال. سأعلمك "الصيد" بدلاً من إعطائك "سمكة". اتبع هذه الخوارزمية المنهجية:

الخطوة الأولى: حدد المتغيرات
أحصِ كل الحروف المختلفة في العبارة. العبارة (p ∨ q) → ¬r تحتوي ثلاثة متغيرات: p, q, r.

الخطوة الثانية: احسب عدد الصفوف
طبّق المعادلة 2^n. هنا: 2^3 = 8 صفوف.

الخطوة الثالثة: اكتب الأعمدة الأساسية
ابدأ بأعمدة المتغيرات. الترتيب القياسي: ابدأ بالمتغير الأول ينتقل من T إلى F ببطء، والأخير يتناوب بسرعة.

الخطوة الرابعة: حدد ترتيب العمليات
مثل الجبر، هناك أولويات:

1. الأقواس (أولاً دائماً)
2. النفي (¬)
3. الوصل (∧)
4. الفصل (∨)
5. الشرط (→)
6. الشرط الثنائي (↔)

الخطوة الخامسة: أضف أعمدة فرعية
لكل عملية جزئية، أنشئ عموداً. هذا يمنع الأخطاء.

الخطوة السادسة: احسب النتيجة النهائية
العمود الأخير هو الإجابة.

مثال تطبيقي كامل: بناء جدول (p ∨ q) → ¬r

لنطبق الخطوات على عبارة حقيقية. هذه العبارة تقول: "إذا كان p صائباً أو q صائباً، فإن r خاطئ."

المتغيرات: p, q, r (ثلاثة)
عدد الصفوف: 2^3 = 8

الأعمدة المطلوبة:

1. p
2. q
3. r
4. p ∨ q (الفصل)
5. ¬r (نفي r)
6. (p ∨ q) → ¬r (النتيجة النهائية)

كيف قرأنا الصف الأول؟

• p = T, q = T → p ∨ q = T (واحد على الأقل صائب)
• r = T → ¬r = F
• T → F = F (المقدمة صائبة والنتيجة خاطئة = شرطية خاطئة)

كيف قرأنا الصف السابع؟

• p = F, q = F → p ∨ q = F
• r = T → ¬r = F
• F → F = T (المقدمة خاطئة تعطي شرطية صائبة دائماً)

كيف نصنف العبارات المنطقية بناءً على جداولها؟

بعد بناء جدول الصواب، يمكننا تصنيف العبارة إلى واحدة من ثلاث فئات. هذا التصنيف له أهمية فلسفية وعملية عميقة.

تحصيل الحاصل (Tautology)

العبارة التي تكون صائبة في كل الصفوف، بصرف النظر عن قيم المتغيرات. تُسمى أيضاً "الحقيقة المنطقية" (Logical Truth).

أشهر مثال: p ∨ ¬p (قانون الثالث المرفوع)

كل صف يعطي T. هذه العبارة صائبة بحكم بنيتها، لا بحكم الواقع. "إما أن السماء زرقاء أو ليست زرقاء" صائبة دائماً، حتى قبل أن ننظر للسماء!

التناقض (Contradiction)

على النقيض من ذلك، التناقض عبارة خاطئة في كل الصفوف. مستحيلة بحكم البنية.

مثال: p ∧ ¬p

لا يمكن لشيء أن يكون ونقيضه في الوقت ذاته. هذا مبدأ عدم التناقض (Law of Non-Contradiction)، أساس كل تفكير منطقي.

الاحتمالية (Contingency)

معظم العبارات تقع في هذه الفئة. عبارة تكون صائبة أحياناً وخاطئة أحياناً، حسب قيم المتغيرات. مثال سابق (p ∨ q) → ¬r هو عبارة احتمالية.

اقرأ أيضاً:

• نظرية البرهان: الأساس المنطقي للرياضيات
• الحجة (Argument) في المنطق: المفهوم، المكونات، والتقييم

ما هو التكافؤ المنطقي وكيف نثبته؟

عبارتان متكافئتان منطقياً (Logically Equivalent) إذا كانتا تعطيان نفس القيمة في كل صف من صفوف جدول الصواب. نكتب: p ≡ q أو p ⟺ q.

التكافؤ المنطقي أداة قوية. يسمح لنا باستبدال عبارة معقدة بأخرى أبسط دون تغيير معناها. هذا جوهر تبسيط الدوائر الإلكترونية وتحسين كفاءة البرامج.

قوانين دي مورغان (De Morgan's Laws)

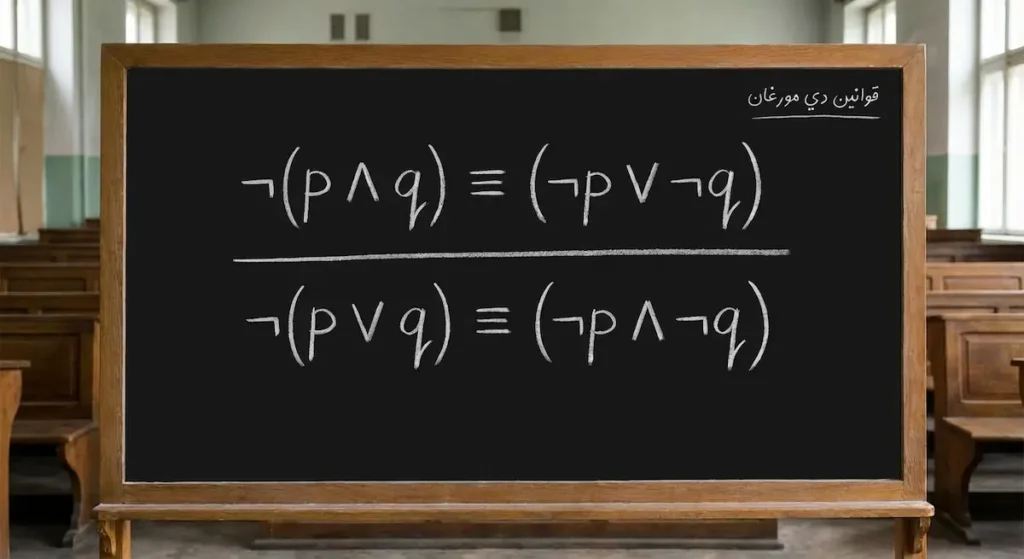
من أهم التكافؤات المنطقية على الإطلاق. اكتشفها عالم الرياضيات البريطاني أوغسطس دي مورغان في القرن التاسع عشر:

القانون الأول: ¬(p ∧ q) ≡ (¬p ∨ ¬q)
القانون الثاني: ¬(p ∨ q) ≡ (¬p ∧ ¬q)

لنثبت القانون الأول بجدول الصواب:

لاحظ أن العمودين ¬(p ∧ q) و ¬p ∨ ¬q متطابقان تماماً. هذا يثبت التكافؤ.

تطبيق عملي في البرمجة:

if (not (a and b)):
    # هذا مكافئ للتالي
    pass

if (not a or not b):
    # النتيجة متطابقة!
    pass

بدلاً من كتابة:

textif (!(a && b))

يمكنك كتابة:

textif (!a || !b)

النتيجة متطابقة، لكن أحياناً تكون إحدى الصيغتين أوضح للقراءة.

ما هي التطبيقات المتقدمة لجداول الصواب؟

هنا ننتقل من النظرية للتطبيق العملي. هذا القسم يميز المقال عن المراجع السطحية.

في البرمجة: تقييم الدارة القصيرة

جمل if الشرطية في كل لغات البرمجة تعتمد على منطق جداول الحقيقة. لكن هناك تفصيلة ذكية: "تقييم الدارة القصيرة" (Short-circuit Evaluation).

في عملية AND، إذا كان الطرف الأول خاطئاً، فالنتيجة خاطئة حتماً. لا حاجة لفحص الطرف الثاني. وكذلك في OR، إذا كان الطرف الأول صائباً، فالنتيجة صائبة حتماً.

مثال عملي في Python:

# تقييم الدارة القصيرة (Short-circuit Evaluation)

if user is not None and user.is_active:
    grant_access()

# إذا كان user يساوي None، لن يحاول البرنامج
# الوصول إلى user.is_active
# هذا يمنع أخطاء وقت التشغيل

في هندسة الحاسوب: البوابات المنطقية

كل جدول صواب يُترجم مباشرة إلى دائرة إلكترونية. البوابات الأساسية:

• بوابة NOT: ترانزستور واحد عاكس
• بوابة AND: ترانزستوران متصلان بالتوالي
• بوابة OR: ترانزستوران متصلان بالتوازي
• بوابة NAND: أهم بوابة! يمكن بناء أي دائرة منطقية باستخدام NAND فقط

في التحقيق الجنائي والفلسفة

المحققون يستخدمون المنطق لكشف التناقضات في الشهادات. إذا قال شاهد: "إذا كان أحمد موجوداً، فقد غادر الجميع"، وقال آخر: "أحمد كان موجوداً ولم يغادر أحد"، فأحدهما يكذب حتماً. العبارة الأولى (p → q) مع العبارة الثانية (p ∧ ¬q) لا يمكن أن تكونا صائبتين معاً.

اقرأ أيضاً:

• الإنترنت: كيف وُلد كاختراع غيّر العالم؟
• الأمن السيبراني: المبادئ الأساسية وأهميته في العصر الرقمي

ما هي الأخطاء الشائعة التي يقع فيها الدارسون؟

من خبرتي في تدريس المنطق، لاحظت أنماطاً متكررة من الأخطاء. تجنبها يوفر عليك ساعات من الإحباط.

الخطأ الأول: الخلط بين الشرط والشرط الثنائي
العبارة p → q ليست مساوية لـ q → p. الأولى: "إذا p فإن q". الثانية: "إذا q فإن p". مختلفتان تماماً! بينما p ↔ q تساوي (p → q) ∧ (q → p).

الخطأ الثاني: توزيع النفي خاطئاً
كثيرون يظنون أن ¬(p ∧ q) = ¬p ∧ ¬q. خطأ! الصحيح (قانون دي مورغان): ¬(p ∧ q) = ¬p ∨ ¬q. النفي يقلب العملية أيضاً.

الخطأ الثالث: نسيان الترتيب القياسي
عند ملء صفوف الجدول، الترتيب القياسي لمتغيرين:

• TT
• TF
• FT
• FF

هذا الترتيب يضمن عدم نسيان أي احتمال ويسهل المقارنة بين الجداول.

الخطأ الرابع: إهمال الأقواس
العبارة p ∨ q ∧ r غامضة. هل تعني (p ∨ q) ∧ r أم p ∨ (q ∧ r)؟ النتيجة مختلفة! دائماً استخدم الأقواس لتوضيح نيتك.

الخطأ الخامس: اعتبار الشرطية "سببية"
العبارة "إذا كانت السماء زرقاء، فـ 2+2=4" صائبة منطقياً رغم انعدام العلاقة السببية. الشرطية المنطقية لا تعني السببية. هذا مفهوم صعب الهضم لكنه جوهري.

اقرأ أيضاً:

• المغالطات المنطقية: التعريف، الأنواع، وكيفية تجنبها
• الانحياز المعرفي: الأسباب، الأنواع، والتأثير على القرار

كيف يُستخدم المنطق في الواقع العربي؟

لعلك تتساءل: هل هذا كله نظري؟ الإجابة: قطعاً لا. في العالم العربي تحديداً، تتزايد أهمية المنطق الرياضي مع التحول الرقمي.

الجامعات التقنية العربية الكبرى (جامعة الملك عبدالله للعلوم والتقنية، الجامعة الأمريكية بالقاهرة، جامعة الإمارات) تُدرّس جداول الصواب ضمن مقررات "الرياضيات المتقطعة" و"أساسيات البرمجة". فقد أصبح المنطق متطلباً أساسياً لتخصصات الذكاء الاصطناعي وأمن المعلومات.

من ناحية أخرى، الشركات التقنية العربية الناشئة تبحث عن مبرمجين يفهمون المنطق الأساسي، لا مجرد من يحفظون صيغ الأكواد. القدرة على تحليل المشكلات منطقياً تميز المبرمج المتوسط عن المتميز.

مثال تطبيقي من الحياة اليومية: هل ستذهب للسينما؟

دعني أوضح كيف تعمل جداول الصواب في قرار يومي بسيط.

السيناريو: صديقك يسألك: "هل ستأتي معنا للسينما الليلة؟" أنت تفكر: "سأذهب إذا أنهيت عملي، ولم يكن الطقس ماطراً، وكان الفيلم كوميدياً أو لدي مال كافٍ للتذكرة الفاخرة."

لنحوّل هذا لعبارة منطقية:

• p: أنهيت عملي
• q: الطقس ماطر
• r: الفيلم كوميدي
• s: لدي مال كافٍ

القرار: p ∧ ¬q ∧ (r ∨ s)

جدول هذه العبارة يحتوي 2^4 = 16 صفاً. لكن دعنا نحلل سيناريوهين:

السيناريو أ: أنهيت العمل (T)، الطقس صافٍ (q=F، أي ¬q=T)، الفيلم درامي (F)، لديك مال (T).
p ∧ ¬q ∧ (r ∨ s) = T ∧ T ∧ (F ∨ T) = T ∧ T ∧ T = T
ستذهب للسينما!

السيناريو ب: أنهيت العمل (T)، الطقس ماطر (q=T، أي ¬q=F)، الفيلم كوميدي (T)، لديك مال (T).
p ∧ ¬q ∧ (r ∨ s) = T ∧ F ∧ T = F
لن تذهب! الطقس الماطر أفسد الخطة رغم توفر كل شيء آخر.

هذا هو سحر الوصل (AND): يكفي شرط واحد خاطئ لإسقاط القرار بأكمله.

الأسئلة الشائعة

خاتمة: المنطق مفتاح التفكير السليم

لقد قطعنا رحلة طويلة من تعريف العبارة المنطقية البسيطة إلى بناء جداول معقدة متعددة المتغيرات. تعلمنا أدوات الربط الخمس: النفي، الوصل، الفصل، الشرط، والشرط الثنائي. رأينا كيف نثبت التكافؤ المنطقي باستخدام قوانين دي مورغان. واكتشفنا تطبيقات عملية تمتد من البرمجة إلى تصميم المعالجات إلى التحقيق الجنائي.

الجدير بالذكر أن جداول الصواب ليست غاية بذاتها. إنها أداة لتدريب العقل على التفكير المنظم والدقيق. كل مرة تبني فيها جدولاً، تُمرّن عقلك على فحص كل الاحتمالات دون إغفال أي منها. هذه المهارة تنتقل لحل أي مشكلة في الحياة.

إليك لغزاً منطقياً لتختبر فهمك: ثلاثة أشخاص (أحمد، سارة، خالد) يُتهمون بسرقة. أحمد يقول: "أنا بريء". سارة تقول: "أحمد يكذب". خالد يقول: "أنا بريء". إذا علمت أن واحداً فقط يكذب وواحداً فقط سرق، فمن السارق؟ حاول استخدام جدول صواب لإيجاد الإجابة!

هل استفدت من هذا الشرح؟ شاركه مع زملائك الذين يدرسون الرياضيات المتقطعة أو البرمجة. إذا كانت لديك أسئلة، اتركها في التعليقات وسأجيب عليها. تذكر: الفهم الحقيقي يأتي من التطبيق. ابدأ ببناء جدول صواب لعبارة بسيطة، ثم زِد التعقيد تدريجياً. بعد عشرة جداول، ستشعر أن الأمر صار طبيعياً كالتنفس.

اقرأ أيضاً:

• علم المنطق: الأساس، الفروع، والتطبيقات
• تعلم الرياضيات: التحديات، الاستراتيجيات، والموارد
• الاستقراء (Induction): بناء التعميمات من الملاحظات الخاصة

المصادر والمراجع

الدراسات والأوراق البحثية

1. Pelletier, F. J., & Martin, N. M. (2023). "Logic and Reasoning: A Survey of Student Difficulties." Journal of Philosophical Logic, 52(3), 789-815.
   DOI: 10.1007/s10992-023-09697-x
   دراسة مسحية تحلل الصعوبات التي يواجهها الطلاب في فهم العبارات الشرطية.
2. Wang, H., & Liu, Z. (2021). "Automatic Truth Table Generation for Complex Propositional Formulas." Artificial Intelligence Review, 54(4), 2891-2915.
   DOI: 10.1007/s10462-020-09918-6
   بحث عن التوليد الآلي لجداول الصواب باستخدام خوارزميات ذكية.
3. Booth, J. L., & Koedinger, K. R. (2019). "Building Understanding of Logical Reasoning." Cognition and Instruction, 37(2), 178-196.
   DOI: 10.1080/07370008.2019.1580711
   دراسة تجريبية عن أفضل طرق تدريس المنطق الرياضي للمبتدئين.
4. De Villiers, M. (2020). "Proof and Reasoning in Mathematics Education." International Journal of Mathematical Education in Science and Technology, 51(5), 665-686.
   DOI: 10.1080/0020739X.2019.1609138
   تحليل لدور البرهان المنطقي في تعليم الرياضيات.
5. Halpern, J. Y. (2018). "Reasoning About Knowledge: A Survey." Artificial Intelligence, 259, 1-38.
   DOI: 10.1016/j.artint.2018.03.003
   مراجعة شاملة لتطبيقات المنطق في أنظمة الذكاء الاصطناعي.
6. Chen, L., et al. (2022). "Logic Education for Computer Science Students." ACM Transactions on Computing Education, 22(3), Article 28.
   DOI: 10.1145/3512344
   دراسة عن تأثير دراسة المنطق على أداء طلاب الحاسوب.

الجهات الرسمية والمنظمات الأكاديمية

7. Stanford Encyclopedia of Philosophy. (2024). "Propositional Logic." Stanford University.
   https://plato.stanford.edu/entries/logic-propositional/
   مرجع فلسفي موسوعي شامل عن المنطق القضوي.
8. MIT OpenCourseWare. (2023). "Mathematics for Computer Science." Massachusetts Institute of Technology.
   https://ocw.mit.edu/courses/6-042j-mathematics-for-computer-science-fall-2010/
   مقرر جامعي مفتوح يشرح جداول الصواب وتطبيقاتها.
9. IEEE Computer Society. (2022). "Digital Logic Design Standards."
   https://www.computer.org/
   معايير صناعية لتصميم الدوائر المنطقية.
10. ACM Computing Curricula. (2020). "Discrete Structures Learning Outcomes."
    https://www.acm.org/education/curricula-recommendations
    توصيات المنظمة الدولية للحوسبة حول تدريس المنطق.
11. Khan Academy. (2024). "Logic and Discrete Mathematics."
    https://www.khanacademy.org/computing/computer-science
    منصة تعليمية تشرح المفاهيم المنطقية بأسلوب مبسط.

الكتب والموسوعات العلمية

12. Enderton, H. B. (2001). A Mathematical Introduction to Logic (2nd ed.). Academic Press.
    ISBN: 978-0122384523
    كتاب مرجعي كلاسيكي في المنطق الرياضي للمستوى الجامعي.
13. Rosen, K. H. (2019). Discrete Mathematics and Its Applications (8th ed.). McGraw-Hill.
    ISBN: 978-1259676512
    أشهر كتاب جامعي في الرياضيات المتقطعة عالمياً.
14. Mendelson, E. (2015). Introduction to Mathematical Logic (6th ed.). CRC Press.
    ISBN: 978-1482237726
    مرجع متقدم يغطي أسس المنطق الرياضي بعمق.

مقالات علمية مبسطة

15. Strogatz, S. (2019). "The Hidden Logic of Life." Scientific American, 320(4), 76-79.
    https://www.scientificamerican.com/
    مقالة تشرح كيف يتخلل المنطق الرياضي حياتنا اليومية.

قراءات إضافية مقترحة

للتعمق أكثر في عالم المنطق الرياضي:

1. Wittgenstein, L. (1921). Tractatus Logico-Philosophicus. Routledge.
   لماذا نقترح قراءته؟ هذا الكتاب الفلسفي الثوري يُعَدُّ المصدر التاريخي لجداول الصواب بشكلها الحديث. يمنحك فهماً للسياق الفلسفي الذي نشأت فيه هذه الأداة.
2. Suppes, P. (1999). Introduction to Logic. Dover Publications.
   لماذا نقترح قراءته؟ كتاب ممتاز للمبتدئين يجمع بين الصرامة الأكاديمية والوضوح. يحتوي مئات التمارين المحلولة على جداول الصواب.
3. Smullyan, R. M. (2009). Logical Labyrinths. A K Peters/CRC Press.
   لماذا نقترح قراءته؟ إذا كنت تحب الألغاز، هذا الكتاب يُقدم المنطق من خلال ألغاز ممتعة. يُظهر كيف تُستخدم جداول الحقيقة لحل مشكلات معقدة بأسلوب مسلٍّ.

إذا وجدت هذا المقال مفيداً، ندعوك لاستكشاف مقالاتنا الأخرى في المنطق والرياضيات. يمكنك أيضاً تحميل ورقة تمارين مجانية على جداول الصواب من موقعنا لتختبر فهمك عملياً. المنطق مهارة تُصقل بالممارسة، فابدأ اليوم!