نظرية الأعداد
-
تمارين

تحدي العباقرة: من أصعب مسائل الرياضيات مع حلولها المفصلة
المسألة 1: حساب التكامل (Calculus) أوجد قيمة التكامل غير المحدد التالي:integral(sqrt(tan(x))) dx الحل:هذا تكامل صعب يتطلب سلسلة من التعويضات الذكية.…
أكمل القراءة » -
رياضيات

ما هي الأعداد الطبيعية: وكيف تشكل أساس الرياضيات؟
تمثل الأعداد الطبيعية الأساس الذي بُنيت عليه الرياضيات منذ فجر الحضارات الإنسانية، فهي أول ما يتعلمه الإنسان في رحلته مع…
أكمل القراءة » -
رياضيات

الأعداد الزوجية: ما هي خصائصها وكيف نتعرف عليها؟
تُمثل الأعداد في عالم الرياضيات لغة كونية تربط بين مختلف العلوم والتطبيقات العملية. إن فهم تصنيفات الأعداد يفتح أمامنا آفاقاً…
أكمل القراءة » -
رياضيات
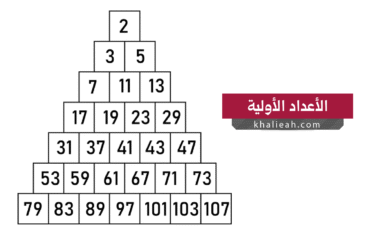
الأعداد الأولية: ما أسرارها وكيف تشكل لبنة بناء الرياضيات؟
تمثل الأعداد الأولية واحدة من أكثر المفاهيم الرياضية إثارة للفضول والتساؤل عبر التاريخ. إنها أعداد بسيطة في تعريفها، لكنها عميقة…
أكمل القراءة » -
رياضيات

الجبر المجرد: ما الذي يجعله أساس الرياضيات الحديثة؟
يمثل الجبر المجرد واحداً من أعمق فروع الرياضيات التي أحدثت ثورة في فهمنا للبنى الرياضية والعلاقات بينها؛ إذ تجاوز هذا…
أكمل القراءة » -
رياضيات
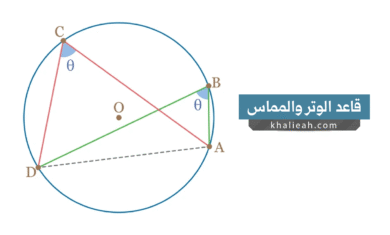
قاعدة الوتر والمماس: كيف نجمع نقاط المنحنيات الرياضية بطريقة هندسية؟
في قلب الرياضيات المتقدمة، توجد فكرة رائعة تربط الهندسة بالجبر بطريقة غير متوقعة. إنها تلك اللحظة التي تكتشف فيها أن…
أكمل القراءة » -
رياضيات

القاسم المشترك الأكبر: من الأساسيات الحسابية إلى التطبيقات المتقدمة
يمثل القاسم المشترك الأكبر حجر زاوية في نظرية الأعداد، ويعتبر من المفاهيم التأسيسية التي تتجاوز حدود الحساب الابتدائي لتصل إلى…
أكمل القراءة » -
رياضيات

القاسم المشترك الأصغر: من الطرق الأساسية إلى التطبيقات الخوارزمية المتقدمة
في عالم الرياضيات، تُبنى المفاهيم المعقدة على أسس بسيطة وأنيقة، ويُعد فهم هذه الأسس هو المفتاح لولوج عوالم أكثر تجريداً…
أكمل القراءة » -
علماء

كارل فريدريش غاوس: أمير الرياضيات وإرثه الخالد في علوم القرن التاسع عشر
في بانثيون العمالقة العلميين، قلة من الأسماء تتردد بقوة وتأثير مثل اسم كارل فريدريش غاوس (1777-1855). يُعد هذا العالم الألماني الفذ، الذي…
أكمل القراءة »
