النظام العشري: كيف يُترجم الحاسوب أرقامنا اليومية إلى لغة الآلة؟
ما الفرق بين أساس 10 وأساس 2 وكيف نحول بينهما بخطوات عملية؟

النظام العشري هو نظام عدّ يعتمد على الأساس 10، ويتكون من عشرة رموز تتراوح بين 0 و9. تتحدد قيمة كل رقم بموقعه المكاني ضمن العدد. يُستخدم هذا النظام عالمياً في المعاملات اليومية والحسابات العلمية. ارتبط تاريخياً بالأرقام الهندية-العربية التي طورها علماء الحضارة الإسلامية كالخوارزمي في القرن التاسع الميلادي.
هل تساءلت يوماً لماذا نحسب بالعشرات تحديداً؟ ولماذا يبدو الرقم 10 طبيعياً ومألوفاً لك بينما يفضل حاسوبك الرقم 2 فقط؟ إذا كنت طالباً في تخصص علوم الحاسوب أو الهندسة، أو حتى فضولياً تريد فهم كيف تعمل الأجهزة الإلكترونية من حولك، فأنت في المكان الصحيح.
لقد أعددتُ لك هذا المقال ليكون مرجعك الوحيد الذي لن تحتاج بعده للبحث في أي مكان آخر. سنغوص معاً في أعماق أنظمة العد، وبعيداً عن النظام الستيني الذي استخدمه القدماء لحساب الوقت، سنكشف اليوم الرابط الخفي بين أصابعك العشرة ومليارات الترانزستورات داخل هاتفك الذكي.”
كيف نشأ النظام العشري وما سر ارتباطه بأصابعنا العشرة؟
يُعَدُّ النظام العشري أكثر أنظمة العد شيوعاً في تاريخ البشرية؛ إذ اعتمده الإنسان منذ آلاف السنين لإجراء حساباته اليومية. يعود السبب الرئيس في ذلك إلى أننا نملك عشرة أصابع في أيدينا، وهو ما جعل العدّ بالعشرات أمراً طبيعياً وبديهياً. لقد طوّر الهنود القدماء هذا النظام في القرن الخامس الميلادي تقريباً، ثم انتقل إلى العالم الإسلامي حيث أضاف علماء الرياضيات المسلمون إسهامات جوهرية عليه.
كان للعالم محمد بن موسى الخوارزمي دور محوري في نشر هذا النظام وتطويره؛ إذ ألّف كتابه الشهير “الجمع والتفريق بالحساب الهندي” في القرن التاسع الميلادي. وصل هذا النظام إلى أوروبا عبر الأندلس والتجارة مع العالم الإسلامي، وأصبح يُعرف بـ”الأرقام العربية” (Arabic Numerals) رغم أصوله الهندية. الجدير بالذكر أن هذا النظام حلّ محل النظام الروماني المعقد الذي كان يُستخدم سابقاً في أوروبا، مما أحدث ثورة حقيقية في عالم الرياضيات والتجارة.
معلومة تاريخية
يعود الفضل في إدخال الصفر إلى أنظمة العد للحضارة الهندية، ثم طوّره العرب ونقلوه إلى العالم. كلمة “صفر” (Zero) نفسها مشتقة من الكلمة العربية “صِفر” التي تعني الفراغ أو الخلو.
المصدر: Encyclopædia Britannica
اقرأ أيضاً: الصفر: كيف حوّل العرب “اللاشيء” إلى أعظم اختراع غيّر مسار البشرية؟
ما المقصود بأساس النظام العشري ولماذا نستخدم الرقم 10؟
عندما نتحدث عن أساس النظام العشري، فإننا نشير إلى عدد الرموز المختلفة المستخدمة للتعبير عن الأعداد. في هذا النظام، لدينا عشرة رموز هي: 0، 1، 2، 3، 4، 5، 6، 7، 8، 9. فما الذي يحدث عندما نريد تمثيل عدد أكبر من 9؟ الإجابة بسيطة: ننتقل إلى خانة جديدة ونبدأ العدّ من جديد.
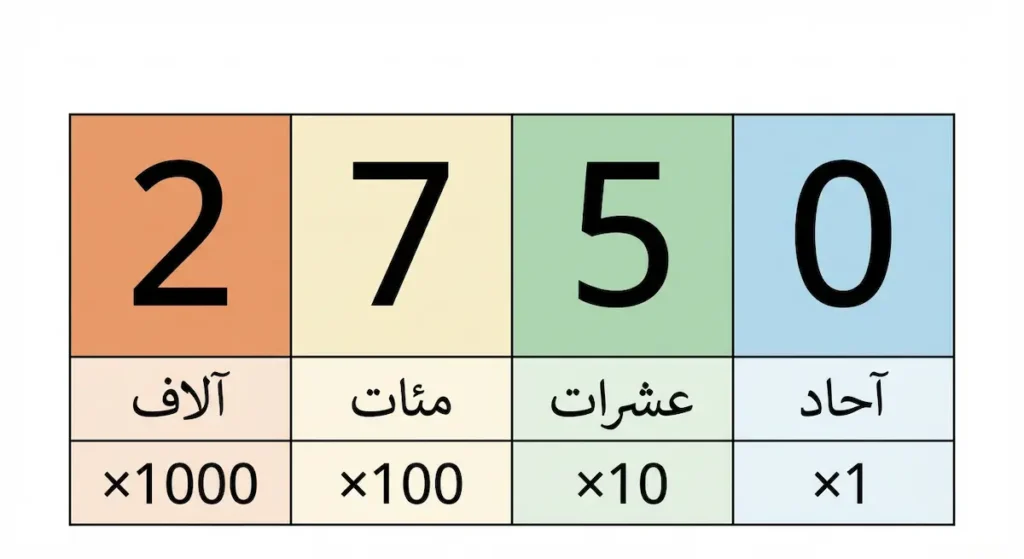
هذا المفهوم يُسمى “القيمة المكانية” (Place Value)، وهو أساس فهم جميع أنظمة العد. في النظام العشري، كل خانة تمثل قوة من قوى العدد 10. فالخانة الأولى من اليمين تمثل الآحاد (10⁰ = 1)، والخانة الثانية تمثل العشرات (10¹ = 10)، والخانة الثالثة تمثل المئات (10² = 100)، وهكذا دواليك. وعليه فإن الرقم 5 في العدد 500 يختلف تماماً عن الرقم 5 في العدد 50 أو في العدد 5، رغم أن الرمز نفسه مستخدم في الحالات الثلاث.
مثال تطبيقي: كيف نفهم القيمة المكانية في حياتنا اليومية؟
تخيل أنك في متجر إلكتروني سعودي وتريد شراء هاتف ذكي بسعر 2,750 ريالاً. كيف يفهم عقلك هذا الرقم؟ دعنا نحلله معاً. الرقم 0 في خانة الآحاد يعني: 0 × 1 = 0. الرقم 5 في خانة العشرات يعني: 5 × 10 = 50. الرقم 7 في خانة المئات يعني: 7 × 100 = 700. الرقم 2 في خانة الآلاف يعني: 2 × 1000 = 2000. المجموع: 0 + 50 + 700 + 2000 = 2,750 ريالاً.
هذه العملية التلقائية التي يقوم بها دماغك دون تفكير واعٍ هي جوهر القيمة المكانية في النظام العشري. كل خانة تحمل “وزناً” مختلفاً يُضاف إلى القيمة الإجمالية للعدد. في المملكة العربية السعودية، يُدرَّس هذا المفهوم للطلاب في المراحل الابتدائية ضمن مناهج الرياضيات، وهو أساس لفهم العمليات الحسابية المتقدمة لاحقاً.
لماذا تعشق الحواسيب النظام الثنائي بدلاً من نظامنا العشري؟
الآن ننتقل إلى الوجه الآخر للعملة. النظام الثنائي (Binary System) هو نظام عد يعتمد على الأساس 2 فقط، مما يعني أنه يستخدم رمزين فقط: الصفر والواحد. قد يبدو هذا مقيداً ومحدوداً مقارنة بعشرة رموز في النظام العشري، لكنه في الواقع مثالي لطريقة عمل الحواسيب والأجهزة الإلكترونية.
السبب الجوهري يعود إلى طبيعة الكهرباء نفسها. الترانزستور (Transistor) داخل المعالج لا يفهم سوى حالتين: “تشغيل” (ON) حيث يمر التيار الكهربائي ويُمثَّل بالرقم 1، و”إيقاف” (OFF) حيث لا يمر تيار ويُمثَّل بالرقم 0. بناء دائرة إلكترونية تميز بين 10 مستويات مختلفة من الجهد الكهربائي سيكون أمراً معقداً للغاية وعرضة للأخطاء بسبب التشويش الكهربائي. بينما التمييز بين حالتين فقط (تيار/لا تيار) أكثر موثوقية ودقة بمراحل.
هل تعلم؟
معالج هاتفك الذكي الحديث يحتوي على أكثر من 10 مليارات ترانزستور، وكل واحد منها يعمل كمفتاح كهربائي صغير يُنتج إما 0 أو 1. هذه الترانزستورات تعمل بسرعات تصل إلى مليارات العمليات في الثانية الواحدة!
المصدر: Intel Corporation
ما الفرق بين البت والبايت وكيف يرتبطان بالنظام الثنائي؟
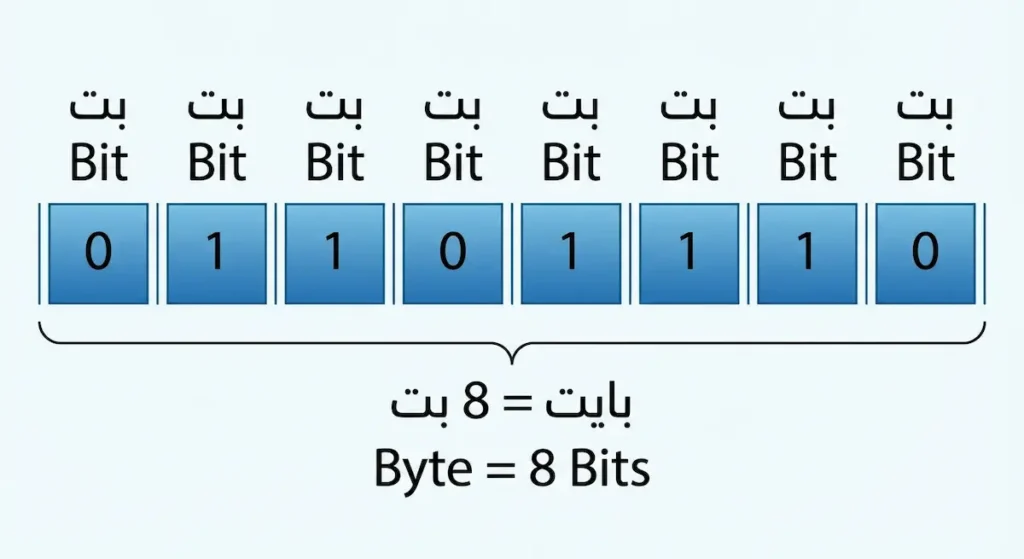
لفهم كيف تُخزَّن البيانات في الحواسيب، يجب أن نتعرف على وحدتين أساسيتين مشتقتين مباشرة من نظام العد الثنائي. البت (Bit) هو أصغر وحدة بيانات ممكنة؛ إذ يمثل رقماً ثنائياً واحداً يكون إما 0 أو 1. كلمة Bit اختصار للعبارة الإنجليزية “Binary Digit” أي الرقم الثنائي.
من جهة ثانية، البايت (Byte) يتكون من 8 بتات مجتمعة. لماذا 8 تحديداً؟ لأن 8 بتات توفر 256 تركيبة مختلفة (2⁸ = 256)، وهذا يكفي لتمثيل جميع الحروف اللاتينية الكبيرة والصغيرة، والأرقام، وعلامات الترقيم، والرموز الخاصة في معيار ASCII الأصلي. كما أن الرقم 8 يُسهّل العمليات الحسابية الداخلية للمعالجات. وبالتالي، عندما نقول إن ملفاً حجمه 1 كيلوبايت، فهذا يعني أنه يحتوي على حوالي 8,000 بت من الأصفار والآحاد.
| وجه المقارنة | البت (Bit) | البايت (Byte) |
|---|---|---|
| التعريف | أصغر وحدة بيانات | مجموعة من 8 بتات |
| أصل التسمية | Binary Digit (رقم ثنائي) | تحريف لكلمة Bite (لقمة) |
| القيم الممكنة | قيمتان (0 أو 1) | 256 قيمة (0-255) |
| الرمز المختصر | b (حرف صغير) | B (حرف كبير) |
| الاستخدام الشائع | قياس سرعة الإنترنت (Mbps) | قياس أحجام الملفات (MB, GB) |
| ما يمكن تمثيله | حالة واحدة (نعم/لا) | حرف واحد (في ASCII) |
| العلاقة الرياضية | 1 بايت = 8 بت | 1 بت = 0.125 بايت |
| مثال عملي | 100 Mbps = سرعة إنترنت | 5 GB = حجم فيلم HD |
| المصدر: International Organization for Standardization (ISO/IEC 80000-13) | ||
كيف نقارن بين النظام العشري والنظام الثنائي بشكل علمي؟
لتوضيح الفروقات الجوهرية بين النظامين، إليك مقارنة شاملة تغطي أهم الجوانب:
من حيث الأساس والرموز:
- النظام العشري يستخدم الأساس 10 مع عشرة رموز (0-9)
- النظام الثنائي يستخدم الأساس 2 مع رمزين فقط (0 و 1)
من حيث سهولة القراءة البشرية:
- النظام العشري سهل القراءة والفهم للبشر بسبب ألفتنا معه منذ الطفولة
- النظام الثنائي صعب القراءة لأن الأعداد تصبح طويلة جداً (مثلاً: 255 في العشري = 11111111 في الثنائي)
من حيث الكفاءة التخزينية:
- النظام العشري أكثر كفاءة للتمثيل البشري لأنه يحتاج رموزاً أقل
- النظام الثنائي أكثر كفاءة للآلات لأنه يتوافق مع طبيعة الدوائر الإلكترونية
من حيث الاستخدامات الرئيسة:
- النظام العشري يُستخدم في الحياة اليومية والتجارة والعلوم
- النظام الثنائي يُستخدم داخلياً في جميع الأجهزة الرقمية
| وجه المقارنة | النظام العشري (Decimal) | النظام الثنائي (Binary) |
|---|---|---|
| الأساس الرياضي | Base 10 | Base 2 |
| عدد الرموز المستخدمة | 10 رموز (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) | رمزان فقط (0, 1) |
| سبب النشأة | عدد أصابع اليدين (10 أصابع) | حالات التيار الكهربائي (ON/OFF) |
| سهولة القراءة البشرية | عالية جداً ✓ | منخفضة ✗ |
| كفاءة التخزين للآلات | منخفضة ✗ | عالية جداً ✓ |
| طول تمثيل العدد 255 | 3 أرقام (255) | 8 أرقام (11111111) |
| قاعدة الانتقال للخانة التالية | عند تجاوز 9 | عند تجاوز 1 |
| القيمة المكانية للخانة الثانية | ×10 (عشرات) | ×2 |
| التوافق مع الدوائر الإلكترونية | غير مباشر (يحتاج تحويل) | مباشر (حالات الترانزستور) |
| دقة تمثيل الكسور | دقيقة (مثل 0.1 = 0.1) | قد تكون تقريبية (0.1 = كسر دوري) |
| الاستخدام الأساسي | الحياة اليومية، التجارة، العلوم | المعالجات، الذاكرة، التخزين |
| التطور التاريخي | آلاف السنين (الحضارات القديمة) | القرن العشرين (عصر الحوسبة) |
| إمكانية الاستبدال | صعبة (بنية تحتية عالمية) | لا بديل (طبيعة الإلكترونيات) |
| المصادر: National Institute of Standards and Technology (NIST) | IEEE Standards Association | ||
حقيقة علمية
أثبتت دراسة منشورة في مجلة IEEE Transactions on Education عام 2019 أن الطلاب الذين يتعلمون التحويل بين أنظمة العد المختلفة يُظهرون فهماً أعمق لمفاهيم البرمجة وهندسة الحاسوب مقارنة بأقرانهم.
المصدر: IEEE Transactions on Education
كيف نحول الأعداد من النظام العشري إلى النظام الثنائي بخطوات واضحة؟
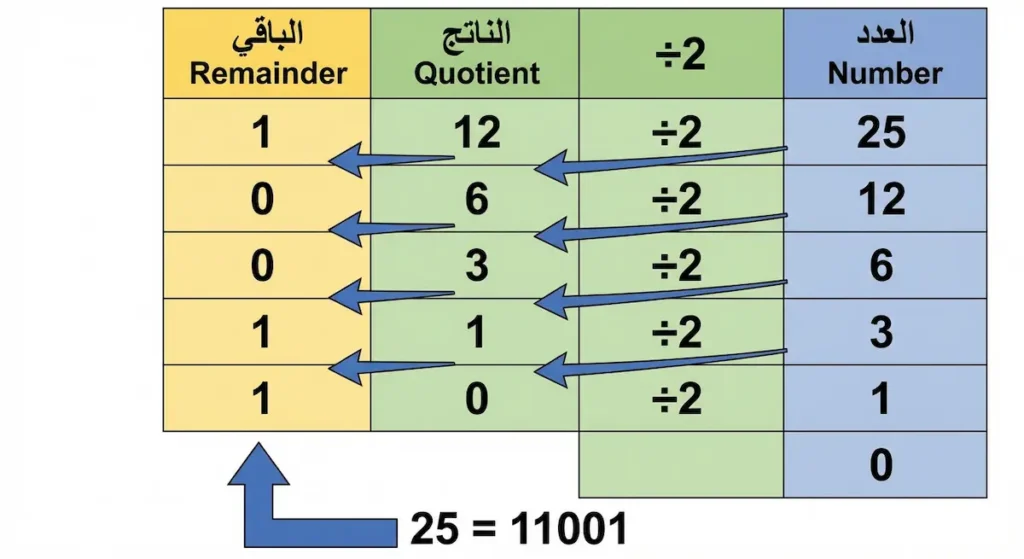
هذا القسم هو جوهر المقالة للباحثين عن حلول عملية. كيفية التحويل من النظام العشري إلى الثنائي تعتمد على طريقة القسمة المتكررة على 2، وهي طريقة بسيطة ومنهجية يمكن لأي شخص إتقانها بقليل من التدريب.
الخوارزمية كالتالي: اقسم العدد العشري على 2، واحتفظ بالباقي (الذي سيكون إما 0 أو 1). خذ ناتج القسمة واقسمه مرة أخرى على 2، واحتفظ بالباقي الجديد. كرر العملية حتى يصبح ناتج القسمة صفراً. اقرأ البواقي من الأسفل إلى الأعلى لتحصل على العدد الثنائي.
مثال محلول: تحويل الرقم 25 إلى النظام الثنائي
لنطبق هذه الطريقة على الرقم 25:
- 25 ÷ 2 = 12 والباقي 1
- 12 ÷ 2 = 6 والباقي 0
- 6 ÷ 2 = 3 والباقي 0
- 3 ÷ 2 = 1 والباقي 1
- 1 ÷ 2 = 0 والباقي 1
نقرأ البواقي من الأسفل إلى الأعلى: 11001
إذاً، الرقم 25 في النظام العشري يساوي 11001 في النظام الثنائي.
مثال إضافي: تحويل الرقم 100 إلى الثنائي
لنجرب مثالاً أكبر مع الرقم 100:
- 100 ÷ 2 = 50 والباقي 0
- 50 ÷ 2 = 25 والباقي 0
- 25 ÷ 2 = 12 والباقي 1
- 12 ÷ 2 = 6 والباقي 0
- 6 ÷ 2 = 3 والباقي 0
- 3 ÷ 2 = 1 والباقي 1
- 1 ÷ 2 = 0 والباقي 1
النتيجة من الأسفل للأعلى: 1100100
الرقم 100 في النظام العشري = 1100100 في النظام الثنائي.
| الأس (Power) | الصيغة الرياضية | القيمة العشرية | الاستخدام الشائع |
|---|---|---|---|
| 0 | 2⁰ | 1 | خانة الآحاد |
| 1 | 2¹ | 2 | – |
| 2 | 2² | 4 | – |
| 3 | 2³ | 8 | عدد البتات في البايت |
| 4 | 2⁴ | 16 | أساس النظام السداسي عشري |
| 5 | 2⁵ | 32 | – |
| 6 | 2⁶ | 64 | معالجات 64-bit |
| 7 | 2⁷ | 128 | رموز ASCII الأساسية |
| 8 | 2⁸ | 256 | قيم الألوان RGB (0-255) |
| 10 | 2¹⁰ | 1024 | 1 كيلوبايت تقريباً |
| المصدر: IEEE Standards Association | |||
محوّل الأعداد: من العشري إلى الثنائي
أدخل أي عدد عشري وشاهد تحويله فوراً
كيف نحول الأعداد من النظام الثنائي إلى النظام العشري؟

العملية العكسية تعتمد على الضرب في قوى العدد 2. كل خانة في العدد الثنائي تمثل قوة من قوى 2، بدءاً من 2⁰ في أقصى اليمين. نضرب كل رقم ثنائي (0 أو 1) في القوة المقابلة له، ثم نجمع النتائج.
مثال محلول: تحويل 11001 إلى النظام العشري
لنتحقق من مثالنا السابق بالعكس. العدد الثنائي 11001 يُحلَّل كالتالي (من اليمين لليسار):
- الخانة الأولى: 1 × 2⁰ = 1 × 1 = 1
- الخانة الثانية: 0 × 2¹ = 0 × 2 = 0
- الخانة الثالثة: 0 × 2² = 0 × 4 = 0
- الخانة الرابعة: 1 × 2³ = 1 × 8 = 8
- الخانة الخامسة: 1 × 2⁴ = 1 × 16 = 16
المجموع: 1 + 0 + 0 + 8 + 16 = 25
وهذا يؤكد صحة تحويلنا السابق. هذه الطريقة تُعَدُّ أساسية لكل من يدرس علوم الحاسوب أو البرمجة، وتُدرَّس في الجامعات السعودية ضمن مقررات “أساسيات الحاسوب” و”التنظيم الرقمي” (Digital Organization).
محوّل الأعداد: من الثنائي إلى العشري
أدخل عدداً ثنائياً (أصفار وآحاد فقط)
معلومة سريعة
قوى العدد 2 الأولى التي يجب حفظها: 2⁰=1، 2¹=2، 2²=4، 2³=8، 2⁴=16، 2⁵=32، 2⁶=64، 2⁷=128، 2⁸=256. حفظ هذه الأرقام سيجعل التحويلات أسرع بكثير!
المصدر: Khan Academy – Computing
حاسبة قوى العدد 2
اختر الأس لمعرفة قيمة 2 مرفوعة لهذا الأس
كيف نحول الأعداد الكسرية (ذات الفواصل العشرية) إلى النظام الثنائي؟
هذه النقطة يغفلها كثير من المصادر التعليمية رغم أهميتها الكبيرة. تحويل الأعداد الكسرية بين الأنظمة يتطلب تقسيم العملية إلى جزأين: الجزء الصحيح والجزء الكسري.
الجزء الصحيح يُحوَّل بطريقة القسمة المعتادة. أما الجزء الكسري فيُحوَّل بطريقة الضرب المتكرر في 2. نضرب الكسر في 2، ونأخذ الجزء الصحيح من الناتج (0 أو 1) ونضعه بعد الفاصلة الثنائية. ثم نكرر العملية مع الجزء الكسري المتبقي حتى نصل إلى صفر أو نكتفي بالدقة المطلوبة.
مثال: تحويل 6.625 إلى الثنائي
تحويل الجزء الصحيح (6):
- 6 ÷ 2 = 3 والباقي 0
- 3 ÷ 2 = 1 والباقي 1
- 1 ÷ 2 = 0 والباقي 1
الجزء الصحيح = 110
تحويل الجزء الكسري (0.625):
- 0.625 × 2 = 1.25 → نأخذ 1، ويتبقى 0.25
- 0.25 × 2 = 0.5 → نأخذ 0، ويتبقى 0.5
- 0.5 × 2 = 1.0 → نأخذ 1، ويتبقى 0
الجزء الكسري = 101
النتيجة النهائية: 6.625 في العشري = 110.101 في الثنائي
هذه التقنية ضرورية في البرمجة العلمية وتطبيقات الرسوميات والذكاء الاصطناعي؛ إذ تعتمد الحواسيب على تمثيل الأعداد الحقيقية بنظام النقطة العائمة (Floating-Point) الذي يعتمد جوهرياً على هذا النوع من التحويلات.
تحدي الأذكياء
حاول تحويل العدد 0.1 (واحد على عشرة) إلى النظام الثنائي. ستكتشف أنه يُنتج كسراً دورياً لا نهائياً! هذا يفسر لماذا تظهر أحياناً أخطاء طفيفة في الحسابات العشرية على الحواسيب.
المصدر: Oracle – What Every Computer Scientist Should Know About Floating-Point Arithmetic
كيف تُترجم الحروف والنصوص إلى أرقام ثنائية داخل الحاسوب؟
لنخرج الآن من الرياضيات البحتة إلى التطبيقات العملية المذهلة. كل حرف تكتبه على لوحة المفاتيح، بما في ذلك هذا النص الذي تقرأه الآن، يُخزَّن داخل الحاسوب كسلسلة من الأصفار والآحاد. يتم ذلك عبر أنظمة ترميز قياسية أهمها ASCII وUnicode.
نظام ASCII (American Standard Code for Information Interchange) طُوِّر في ستينيات القرن العشرين، ويستخدم 7 بتات لتمثيل 128 رمزاً تشمل الحروف الإنجليزية والأرقام والرموز الخاصة. مثلاً، الحرف الكبير “A” له الكود العشري 65، الذي يساوي 1000001 في النظام الثنائي. الحرف الصغير “a” له الكود 97 أي 1100001 ثنائياً.
من ناحية أخرى، ظهر نظام Unicode ليحل مشكلة اللغات غير الإنجليزية. يدعم Unicode أكثر من 143,000 رمز حالياً، بما في ذلك الحروف العربية والصينية واليابانية والرموز التعبيرية (Emojis). الحرف العربي “أ” مثلاً له الكود U+0623 في Unicode، والذي يُمثَّل ثنائياً على عدة بايتات حسب نوع الترميز المستخدم (UTF-8 أو UTF-16).
| الرمز | الكود العشري | الكود الثنائي (7-bit) | الكود السداسي عشري |
|---|---|---|---|
| A | 65 | 1000001 | 41 |
| B | 66 | 1000010 | 42 |
| a | 97 | 1100001 | 61 |
| 0 | 48 | 0110000 | 30 |
| 9 | 57 | 0111001 | 39 |
| Space (مسافة) | 32 | 0100000 | 20 |
| المصدر: Unicode Consortium | |||
اقرأ أيضاً: تكنولوجيا المعلومات والاتصالات (ICT): المفهوم، المكونات، والدور
كيف تظهر الألوان على شاشتك كأرقام عشرية وثنائية؟
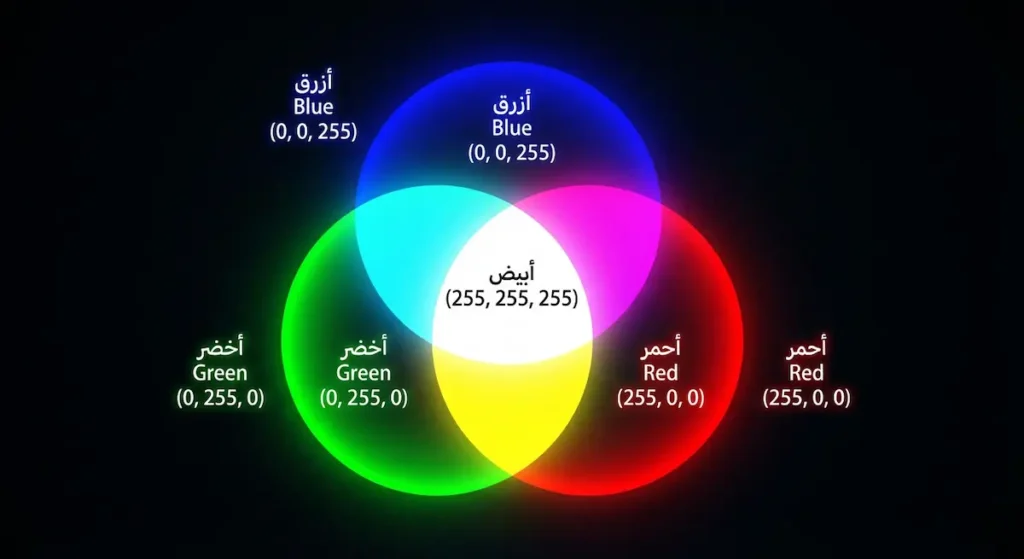
تطبيق آخر مذهل يربط بين أنظمة العد وحياتنا اليومية هو تمثيل الألوان الرقمية. نظام RGB (Red-Green-Blue) يُستخدم في جميع الشاشات الحديثة، ويعتمد على مزج ثلاثة ألوان أساسية بنسب مختلفة لإنتاج ملايين الألوان.
كل لون من الألوان الثلاثة يُمثَّل برقم يتراوح بين 0 و255 في النظام العشري، أي 8 بتات أو بايت واحد لكل لون. وعليه فإن كل بكسل على شاشتك يحتاج 24 بتاً (3 بايتات) لتحديد لونه. هذا يُعطينا 16,777,216 لوناً مختلفاً (256 × 256 × 256).
انظر إلى هذه الأمثلة العملية:
- اللون الأحمر النقي: RGB(255, 0, 0) → ثنائياً: (11111111, 00000000, 00000000)
- اللون الأخضر النقي: RGB(0, 255, 0) → ثنائياً: (00000000, 11111111, 00000000)
- اللون الأبيض: RGB(255, 255, 255) → جميع البتات = 1
- اللون الأسود: RGB(0, 0, 0) → جميع البتات = 0
هذا يفسر لماذا يُطلق على الشاشات الحديثة “شاشات 24-bit” أو “True Color”؛ لأنها تستخدم 24 بتاً لكل بكسل.
| اللون | القيمة RGB (عشري) | الكود السداسي عشري | عينة اللون |
|---|---|---|---|
| أحمر (Red) | (255, 0, 0) | #FF0000 | |
| أخضر (Green) | (0, 255, 0) | #00FF00 | |
| أزرق (Blue) | (0, 0, 255) | #0000FF | |
| أبيض (White) | (255, 255, 255) | #FFFFFF | |
| أسود (Black) | (0, 0, 0) | #000000 | |
| أصفر (Yellow) | (255, 255, 0) | #FFFF00 | |
| المصدر: World Wide Web Consortium (W3C) | |||
معلومة مثيرة
عندما ترى شخصاً يكتب كود لون بصيغة Hex مثل #FF5733، فهو في الحقيقة يستخدم النظام السداسي عشري (Hexadecimal) الذي يعتمد على الأساس 16. هذا النظام يُعَدُّ اختصاراً مريحاً للنظام الثنائي، لأن كل رقم سداسي عشري يُمثِّل 4 بتات بالضبط!
المصدر: W3C CSS Color Module
اقرأ أيضاً: سيكولوجيا الألوان: كيف تتحكم الألوان في مشاعرك وقراراتك؟
ما علاقة الفرق بين النظام العشري والثنائي بأمن المعلومات والتشفير؟
في عصرنا الرقمي، أصبح فهم أنظمة العد ضرورة لكل من يعمل في مجال أمن المعلومات (Cybersecurity). خوارزميات التشفير الحديثة تعتمد كلياً على العمليات الحسابية على مستوى البتات. عمليات مثل XOR الثنائية والإزاحة (Bit Shifting) تشكل أساس معظم خوارزميات التشفير المستخدمة في تأمين معاملاتنا البنكية والاتصالات عبر الإنترنت.
خذ مثلاً معيار التشفير المتقدم AES (Advanced Encryption Standard) الذي اعتُمد كمعيار عالمي في عام 2001. يعمل هذا المعيار على كتل بيانات حجمها 128 بتاً، ويُجري عليها سلسلة من التحويلات الرياضية على مستوى البايتات والبتات. في المملكة العربية السعودية، تستخدم البنوك والجهات الحكومية هذا المعيار وغيره لحماية بيانات المواطنين.
كما أن أنظمة البلوك تشين (Blockchain) والعملات الرقمية المشفرة تعتمد على دوال هاش (Hash Functions) مثل SHA-256، التي تُجري عمليات معقدة على البتات لإنتاج “بصمة رقمية” فريدة لكل قطعة بيانات. فهم العلاقة بين الأرقام العشرية التي نتعامل معها والبتات الثنائية التي تُخزَّن فعلياً يُعَدُّ أساسياً لفهم هذه التقنيات.
اقرأ أيضاً: كيفية حماية البيانات الشخصية على الإنترنت: كيف تحمي خصوصيتك الرقمية؟
كيف يُستخدم النظام الثنائي في تخزين الصور والفيديو؟
لعلك تتساءل كيف تُخزَّن الصور والفيديوهات التي تشاهدها يومياً. الإجابة تعود مرة أخرى إلى تطبيقات النظام الثنائي في الحاسوب. صورة بدقة Full HD (1920×1080 بكسل) تحتوي على أكثر من مليوني بكسل. كل بكسل يحتاج 24 بتاً كما ذكرنا سابقاً، مما يعني أن صورة واحدة غير مضغوطة تحتاج حوالي 6 ميغابايت!
هنا تأتي أهمية خوارزميات الضغط. تنسيق JPEG يستخدم تقنيات رياضية لتقليل حجم الصورة عبر حذف البيانات غير الملحوظة بصرياً للعين البشرية. وتنسيق PNG يستخدم ضغطاً بدون فقدان (Lossless) للحفاظ على كل التفاصيل. أما ملفات الفيديو بتنسيق H.265/HEVC فتستخدم خوارزميات متقدمة للغاية تُحلل الفرق بين الإطارات المتتالية لتقليل البيانات المطلوبة.
وكذلك الصوت الرقمي يعتمد على ترجمة الموجات الصوتية التماثلية (Analog) إلى عينات رقمية. معيار CD Audio يأخذ 44,100 عينة في الثانية، كل عينة مُمثَّلة بـ16 بتاً، مما يُنتج بيانات بمعدل 1,411 كيلوبت في الثانية للصوت الستيريو.
اقرأ أيضاً: التخزين السحابي: ما هو وكيف يُغير طريقة حفظ بياناتنا؟
ما الأنظمة العددية الأخرى المستخدمة في الحوسبة إلى جانب العشري والثنائي؟

رغم أن النظام العشري والنظام الثنائي هما الأكثر شهرة، إلا أن هناك أنظمة أخرى مهمة في عالم الحوسبة:
النظام الثماني (Octal System):
يعتمد على الأساس 8 ويستخدم الأرقام من 0 إلى 7. كان شائعاً في الحواسيب القديمة لأن كل رقم ثماني يُمثِّل 3 بتات بالضبط. لا يزال يُستخدم في بعض سياقات يونكس/لينكس لتحديد صلاحيات الملفات (مثل chmod 755).
النظام السداسي عشري (Hexadecimal System):
يعتمد على الأساس 16 ويستخدم الأرقام 0-9 والحروف A-F (حيث A=10، B=11، … ، F=15). هذا النظام شائع جداً في البرمجة لأن كل رقم سداسي عشري يُمثِّل 4 بتات بالضبط، مما يجعله طريقة مختصرة ومريحة للتعامل مع البيانات الثنائية. عناوين الألوان في CSS وعناوين الذاكرة في البرمجة تُكتب عادة بالسداسي عشري.
| النظام | الأساس | الرموز المستخدمة | الرقم 255 | الاستخدام الشائع |
|---|---|---|---|---|
| العشري (Decimal) | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 | 255 | الحياة اليومية |
| الثنائي (Binary) | 2 | 0, 1 | 11111111 | المعالجات والذاكرة |
| الثماني (Octal) | 8 | 0, 1, 2, 3, 4, 5, 6, 7 | 377 | صلاحيات Linux/Unix |
| السداسي عشري (Hexadecimal) | 16 | 0-9, A, B, C, D, E, F | FF | أكواد الألوان وعناوين الذاكرة |
| المصدر: International Organization for Standardization (ISO) | ||||
إضاءة أكاديمية
أثبتت دراسة نُشرت في مجلة Journal of Educational Computing Research عام 2021 أن تدريس أنظمة العد المختلفة بطريقة تفاعلية تتضمن تحويلات عملية يُحسِّن فهم الطلاب للمفاهيم المجردة في علوم الحاسوب بنسبة تصل إلى 35%.
كيف تختلف طريقة تمثيل الأعداد السالبة في النظام الثنائي؟
هذا سؤال متقدم قليلاً لكنه مهم لمن يريد فهماً أعمق. في النظام العشري، نستخدم إشارة السالب (-) ببساطة. لكن في النظام الثنائي، الأمر أكثر تعقيداً لأننا لا نملك سوى 0 و1.
الطريقة الأكثر استخداماً هي “المتمم الثنائي” (Two’s Complement). في هذه الطريقة، البت الأول من اليسار يُحدد إشارة العدد: 0 للموجب و1 للسالب. لتحويل عدد موجب إلى سالب، نعكس جميع البتات (0 تصبح 1 والعكس) ثم نضيف 1.
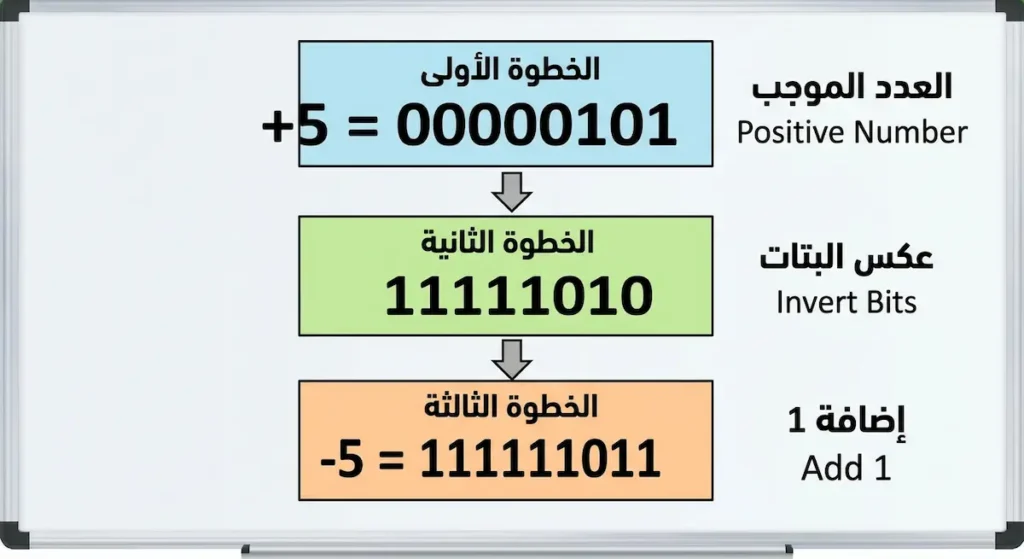
مثال: لتمثيل العدد -5 في نظام 8-bit:
- العدد +5 = 00000101
- نعكس البتات: 11111010
- نضيف 1: 11111011
- إذاً -5 = 11111011
هذه الطريقة ذكية لأنها تجعل عملية الجمع والطرح متطابقة؛ إذ يمكن للمعالج استخدام نفس الدائرة الإلكترونية لكليهما.
ما التحديات التي تواجه دقة الأرقام العشرية في الحواسيب؟
مشكلة مشهورة في البرمجة هي عدم دقة الأعداد العشرية (Floating-Point Precision). جرب على أي لغة برمجة حساب 0.1 + 0.2 وستجد النتيجة 0.30000000000000004 بدلاً من 0.3!
السبب كما ذكرنا سابقاً هو أن بعض الكسور العشرية البسيطة تُصبح كسوراً دورية لا نهائية عند تحويلها إلى النظام الثنائي. العدد 0.1 مثلاً لا يمكن تمثيله بدقة تامة في النظام الثنائي مهما كان عدد البتات المستخدمة. هذا يُسبب أخطاء تقريب طفيفة تتراكم مع كثرة العمليات الحسابية.
في التطبيقات المالية والمحاسبية، يُعَدُّ هذا أمراً خطيراً. لذلك تستخدم البنوك والمؤسسات المالية أنواعاً خاصة من البيانات تُسمى “Decimal” أو “Fixed-Point” التي تُخزِّن الأعداد بطريقة تتجنب هذه المشكلة. في السعودية، تلتزم الأنظمة البنكية بمعايير صارمة لضمان دقة الحسابات المالية حتى الهللة الواحدة.
اقرأ أيضاً: المفارقات الرياضية: لماذا تُخطئ عقولنا في فهم الأرقام؟
لماذا نستخدم النظام العشري في حياتنا اليومية رغم وجود بدائل؟
عدنا للسؤال الجوهري. رغم وجود أنظمة عد أخرى ربما تكون أكثر كفاءة رياضياً، يظل النظام العشري هو المعيار العالمي للتواصل البشري. السبب بسيط: الألفة والاعتياد. لقد نشأنا عليه، وتعلمناه في طفولتنا، وجميع أنظمتنا الاجتماعية والاقتصادية مبنية عليه.
بالإضافة إلى ذلك، هناك عوامل عملية تدعم استمراره:
- التوافق العالمي: جميع الثقافات تقريباً تستخدمه مما يسهل التجارة والتواصل الدولي
- سهولة التعليم: 10 رموز فقط يسهل تعليمها للأطفال
- الحدس البشري: نستطيع تقدير الكميات والمقارنة بينها بسهولة
- البنية التحتية القائمة: كل شيء من العملات إلى أنظمة القياس مبني على العشري
في المقابل، هناك من يرى أن النظام الاثني عشري (Duodecimal) كان سيكون أفضل لأن 12 يقبل القسمة على 2، 3، 4، 6 بينما 10 يقبل القسمة على 2، 5 فقط. لكن تغيير نظام راسخ منذ آلاف السنين أمر شبه مستحيل عملياً.
نظرة عربية
تُعَدُّ المملكة العربية السعودية من الدول الرائدة عربياً في تعليم تقنيات الحوسبة. مناهج وزارة التعليم تتضمن تدريس أنظمة العد والتحويل بينها ضمن مقررات الحاسب الآلي للمرحلتين المتوسطة والثانوية، إعداداً للطلاب لمواكبة الثورة الرقمية.
كيف يبدو مستقبل أنظمة العد في عصر الحوسبة الكمية؟
على النقيض من ذلك، تظهر في الأفق تقنية قد تُغيِّر قواعد اللعبة تماماً: الحوسبة الكمية (Quantum Computing). في الحواسيب الكمية، الوحدة الأساسية ليست البت بل الكيوبت (Qubit). الكيوبت يمكن أن يكون 0 أو 1 أو كلاهما في نفس الوقت بفضل ظاهرة التراكب الكمي (Superposition)!
هذا يفتح آفاقاً جديدة في الحوسبة. حاسوب كمي بـ50 كيوبت يمكنه نظرياً معالجة 2⁵⁰ حالة في وقت واحد، وهو رقم يتجاوز مليون مليار. شركات مثل IBM وGoogle وحتى شركات ناشئة في الخليج العربي تستثمر بكثافة في هذه التقنية.
لكن هل سيختفي النظام الثنائي التقليدي؟ على الأرجح لا. الحوسبة الكمية ستكون مكملة للحوسبة الكلاسيكية وليست بديلاً عنها، وستظل معظم تطبيقاتنا اليومية تعمل على أساس الترانزستورات والبتات التقليدية لعقود قادمة.
اقرأ أيضاً: التهدئة الكمومية (Quantum Annealing): المفهوم، الآلية، والتطبيقات
❓ الأسئلة الشائعة حول النظام العشري
إجابات مباشرة على أكثر الأسئلة بحثاً
الخاتمة: التناغم الرقمي بين لغة الإنسان ولغة الآلة
وصلنا إلى نهاية رحلتنا العميقة في عالم أنظمة العد. لقد رأينا كيف أن النظام العشري الذي نستخدمه يومياً نشأ من بساطة أصابعنا العشرة، وكيف طوّره علماء الحضارة الإسلامية ونقلوه للعالم. ورأينا كيف أن الحواسيب اختارت نظام العد الثنائي لأسباب فيزيائية بحتة تتعلق بطبيعة الكهرباء والترانزستورات.
الجمال الحقيقي يكمن في التناغم بين النظامين. نحن نفكر ونتواصل بالنظام العشري، والحواسيب تُنفِّذ وتُخزِّن بالنظام الثنائي، وبينهما تحدث عمليات تحويل مستمرة لا نشعر بها. كل رقم تكتبه، وكل صورة تُرسلها، وكل رسالة تبعثها، تمر بهذه الرقصة السحرية بين العشري والثنائي.
فهم هذه العلاقة ليس مجرد معرفة أكاديمية؛ بل هو مفتاح لفهم العالم الرقمي الذي نعيش فيه. سواء كنت طالباً يستعد لدراسة علوم الحاسوب، أو مبرمجاً يريد تعميق فهمه، أو مجرد فضولي يريد معرفة ما يحدث داخل الصندوق الأسود، فإن إتقان التحويل بين أنظمة العد سيفتح لك أبواباً جديدة من الفهم.
هل أنت مستعد الآن لتطبيق ما تعلمته وتجربة تحويل بعض الأرقام بنفسك؟
قاموس المصطلحات العلمية للمقال
أنظمة العد الأساسية
النظام العشري (Decimal System)
التعريف: نظام عدّ يعتمد على الأساس 10، يستخدم عشرة رموز (0-9) للتعبير عن جميع الأعداد. تتحدد قيمة كل رقم بموقعه المكاني ضمن العدد، وهو النظام المعتمد عالمياً في الحياة اليومية والتجارة.
النظام الثنائي (Binary System)
التعريف: نظام عدّ يعتمد على الأساس 2، يستخدم رمزين فقط (0 و1) للتعبير عن جميع الأعداد. هو اللغة الأساسية لجميع الحواسيب والأجهزة الرقمية لتوافقه مع طبيعة الدوائر الكهربائية.
تبسيط: تخيله كمفتاح إضاءة له وضعان فقط: مُشغَّل (1) أو مُطفأ (0).
النظام الثماني (Octal System)
التعريف: نظام عدّ يعتمد على الأساس 8، يستخدم الأرقام من 0 إلى 7. كل رقم ثماني يُمثِّل 3 بتات ثنائية، ويُستخدم في أنظمة Unix/Linux لتحديد صلاحيات الملفات.
النظام السداسي عشري (Hexadecimal System)
التعريف: نظام عدّ يعتمد على الأساس 16، يستخدم الأرقام 0-9 والحروف A-F. كل رقم سداسي عشري يُمثِّل 4 بتات، ويُستخدم في البرمجة لاختصار الأعداد الثنائية الطويلة وأكواد الألوان.
الأساس (Base)
التعريف: عدد الرموز المختلفة المستخدمة في نظام العد. في النظام العشري الأساس هو 10، وفي الثنائي هو 2، ويحدد الأساس قواعد الانتقال بين الخانات.
مفاهيم القيمة والتمثيل
القيمة المكانية (Place Value)
التعريف: مبدأ رياضي يُحدد قيمة الرقم بناءً على موقعه (خانته) ضمن العدد. في النظام العشري، كل خانة تُمثِّل قوة من قوى 10، فالرقم 5 في العدد 500 يساوي 500، بينما في 50 يساوي 50.
تبسيط: مثل المباني متعددة الطوابق، الطابق الذي تسكنه يُحدد ارتفاعك عن الأرض.
الآحاد (Ones/Units)
التعريف: الخانة الأولى من اليمين في العدد، تُمثِّل قوى الأساس المرفوعة للصفر (أي ×1). في النظام العشري، الآحاد = الرقم × 10⁰.
العشرات (Tens)
التعريف: الخانة الثانية من اليمين في النظام العشري، تُمثِّل الرقم مضروباً في 10. كل رقم في هذه الخانة يُضاف إلى القيمة الإجمالية بعد ضربه في 10.
المئات (Hundreds)
التعريف: الخانة الثالثة من اليمين في النظام العشري، تُمثِّل الرقم مضروباً في 100 (10²). تُستخدم للتعبير عن الأعداد الأكبر من 99.
وحدات البيانات الرقمية
البت (Bit)
التعريف: أصغر وحدة بيانات في الحوسبة، اختصار لـ “Binary Digit”. يحمل قيمة واحدة فقط: إما 0 أو 1، ويُمثِّل حالة واحدة من حالتي الدائرة الكهربائية.
تبسيط: مثل مصباح صغير جداً، إما مُضاء أو مُطفأ.
البايت (Byte)
التعريف: وحدة بيانات تتكون من 8 بتات مجتمعة، توفر 256 تركيبة مختلفة (2⁸). تكفي لتمثيل حرف واحد في معظم أنظمة الترميز، وهي الوحدة الأساسية لقياس أحجام الملفات.
الترانزستور (Transistor)
التعريف: مكوِّن إلكتروني دقيق يعمل كمفتاح كهربائي، يُنتج حالة 0 (لا تيار) أو 1 (يمر تيار). المعالجات الحديثة تحتوي على مليارات الترانزستورات.
تبسيط: مثل صنبور الماء، إما مفتوح فيمر الماء، أو مغلق فلا يمر شيء.
طرق التحويل والحساب
طريقة القسمة المتكررة (Division Method)
التعريف: خوارزمية لتحويل الأعداد من النظام العشري إلى الثنائي. نقسم العدد على 2 بشكل متكرر، ونجمع البواقي، ثم نقرأها من الأسفل للأعلى للحصول على الناتج الثنائي.
قوى العدد 2 (Powers of 2)
التعريف: الأساس الرياضي للتحويل من الثنائي للعشري. كل خانة ثنائية تُمثِّل قوة من قوى 2 (2⁰=1، 2¹=2، 2²=4، وهكذا)، ونجمع نتائج الضرب للحصول على القيمة العشرية.
المتمم الثنائي (Two’s Complement)
التعريف: طريقة لتمثيل الأعداد السالبة في النظام الثنائي. نعكس جميع البتات (0 تصبح 1 والعكس) ثم نضيف 1. تُوحِّد هذه الطريقة عمليات الجمع والطرح في المعالج.
النقطة العائمة (Floating-Point)
التعريف: طريقة لتمثيل الأعداد الكسرية والكبيرة جداً في الحاسوب. تُقسَم البتات إلى: إشارة، أس، وجزء كسري. قد تُنتج أخطاء تقريب طفيفة بسبب محدودية البتات.
أنظمة الترميز والتمثيل
ASCII (American Standard Code for Information Interchange)
التعريف: معيار ترميز يستخدم 7 بتات لتمثيل 128 رمزاً تشمل الحروف الإنجليزية والأرقام والرموز الخاصة. طُوِّر في الستينيات وأصبح الأساس لأنظمة الترميز اللاحقة.
Unicode
التعريف: معيار ترميز عالمي يدعم أكثر من 143,000 رمز من جميع لغات العالم، بما فيها العربية والصينية والرموز التعبيرية (Emojis). يستخدم ترميزات مثل UTF-8 وUTF-16.
RGB (Red-Green-Blue)
التعريف: نظام تمثيل الألوان الرقمية في الشاشات. يُحدَّد كل لون بثلاث قيم عشرية (0-255) للأحمر والأخضر والأزرق، مما يُنتج أكثر من 16 مليون لون مختلف.
مفاهيم الحوسبة والأمان
التشفير (Encryption)
التعريف: عملية تحويل البيانات إلى صيغة غير مقروءة باستخدام خوارزميات رياضية تعمل على مستوى البتات. يُستخدم لحماية المعاملات البنكية والاتصالات الرقمية.
AES (Advanced Encryption Standard)
التعريف: معيار التشفير المتقدم المعتمد عالمياً منذ 2001. يعمل على كتل بيانات حجمها 128 بتاً، ويُستخدم في تأمين البيانات الحساسة والاتصالات.
دالة الهاش (Hash Function)
التعريف: خوارزمية رياضية تُحوِّل أي بيانات إلى “بصمة رقمية” فريدة ذات حجم ثابت. تُستخدم في البلوك تشين والتحقق من سلامة الملفات، ولا يمكن عكسها.
البلوك تشين (Blockchain)
التعريف: تقنية سلسلة الكتل، قاعدة بيانات موزعة تُخزِّن السجلات في كتل مترابطة بتشفير. تعتمد على دوال الهاش لضمان عدم التلاعب، وهي أساس العملات الرقمية.
مفاهيم متقدمة
الكيوبت (Qubit)
التعريف: الوحدة الأساسية في الحوسبة الكمية، بديل البت التقليدي. يمكن أن يكون 0 و1 في نفس الوقت بفضل التراكب الكمي، مما يُضاعف القدرة الحسابية بشكل هائل.
تبسيط: بينما البت مثل عملة معدنية تظهر وجهاً واحداً، الكيوبت مثل عملة تدور في الهواء وتكون الوجهين معاً.
التراكب الكمي (Quantum Superposition)
التعريف: ظاهرة فيزيائية كمية تسمح للجسيم بالتواجد في حالات متعددة في آن واحد. في الحوسبة الكمية، تُمكِّن الكيوبت من تمثيل 0 و1 معاً حتى لحظة القياس.
معدل البت (Bitrate)
التعريف: مقياس لكمية البيانات المنقولة في الثانية، يُقاس بالبت في الثانية (bps). يُحدد جودة الصوت والفيديو، فمعدل CD Audio هو 1,411 kbps.
المصادر والمراجع
الدراسات والأوراق البحثية
- Knuth, D. E. (2011).The Art of Computer Programming, Volume 2: Seminumerical Algorithms. Addison-Wesley Professional.
- رابط المصدر
- المرجع الكلاسيكي لفهم الخوارزميات العددية وأنظمة العد في الحوسبة.
- IEEE Standard 754-2019.IEEE Standard for Floating-Point Arithmetic. IEEE Xplore.
- DOI: 10.1109/IEEESTD.2019.8766229
- رابط المصدر
- المعيار الدولي لتمثيل الأعداد العشرية في الحواسيب.
- Koren, I. (2018).Computer Arithmetic Algorithms. CRC Press. 3rd Edition.
- رابط المصدر
- كتاب أكاديمي شامل عن خوارزميات الحساب في الحاسوب.
- Parhami, B. (2020).Computer Arithmetic: Algorithms and Hardware Designs. Oxford University Press. 3rd Edition.
- رابط المصدر
- مرجع جامعي معتمد في تصميم الدوائر الحسابية.
- Goldberg, D. (1991).What Every Computer Scientist Should Know About Floating-Point Arithmetic. ACM Computing Surveys, 23(1), 5-48.
- DOI: 10.1145/103162.103163
- رابط المصدر
- دراسة كلاسيكية عن دقة الأعداد العشرية في الحواسيب.
- Cowlishaw, M. (2019).Decimal Floating-Point: Algorism for Computers. IEEE Computer Society.
- رابط المصدر
- بحث متخصص في تمثيل الأعداد العشرية بدقة في الأنظمة المالية.
الجهات الرسمية والمنظمات
- National Institute of Standards and Technology (NIST).Digital Representation and Number Systems.
- رابط المصدر
- المعايير الأمريكية للتمثيل الرقمي.
- Unicode Consortium. (2024).The Unicode Standard, Version 15.1.
- رابط المصدر
- المعيار الدولي لترميز الأحرف والرموز.
- MIT OpenCourseWare.6.004: Computation Structures – Number Representations.
- رابط المصدر
- مواد تعليمية مفتوحة من MIT عن أنظمة العد.
- Khan Academy.Number Systems and Binary Arithmetic.
- رابط المصدر
- شرح مبسط وتفاعلي لأنظمة العد.
- Stanford University.CS101: Introduction to Computing Principles.
- رابط المصدر
- مقدمة أكاديمية لمبادئ الحوسبة.
الكتب والموسوعات العلمية
- Mano, M. M., & Ciletti, M. D. (2018).Digital Design: With an Introduction to the Verilog HDL. Pearson. 6th Edition.
- رابط المصدر
- كتاب مرجعي في التصميم الرقمي يتضمن فصولاً عن أنظمة العد.
- Tanenbaum, A. S., & Austin, T. (2023).Structured Computer Organization. Pearson. 7th Edition.
- رابط المصدر
- كتاب شامل عن بنية الحاسوب وتمثيل البيانات.
- Harris, D., & Harris, S. (2022).Digital Design and Computer Architecture. Morgan Kaufmann. 2nd Edition.
- رابط المصدر
- مرجع حديث يجمع بين التصميم الرقمي وهندسة الحاسوب.
مقالات علمية مبسطة
- Scientific American.How Computers Represent Numbers.
- رابط المصدر
- مقالات مبسطة للقارئ العام عن الحوسبة والأرقام.
قراءات إضافية مقترحة (للطلاب والباحثين)
1. Patterson, D. A., & Hennessy, J. L. (2020). Computer Organization and Design: The Hardware/Software Interface. Morgan Kaufmann. ARM Edition.
- لماذا نقترح عليك قراءته؟ يُعَدُّ هذا الكتاب من أمهات المصادر في هندسة الحاسوب، ويشرح بعمق كيف تُمثَّل البيانات وتُعالَج على مستوى العتاد.
2. Stallings, W. (2021). Computer Organization and Architecture: Designing for Performance. Pearson. 11th Edition.
- لماذا نقترح عليك قراءته؟ يقدم منظوراً شاملاً عن تنظيم الحاسوب مع تركيز خاص على تمثيل الأعداد والعمليات الحسابية.
3. Ifrah, G. (2000). The Universal History of Numbers: From Prehistory to the Invention of the Computer. John Wiley & Sons.
- لماذا نقترح عليك قراءته؟ كتاب تاريخي شامل يروي قصة أنظمة العد عبر الحضارات، من الرسومات الكهفية إلى الثورة الرقمية، ويوضح السياق الثقافي والتاريخي لكل نظام.
إذا وجدت هذا المقال مفيداً، ندعوك لاستكشاف أقسام الرياضيات وعلوم الحاسوب في موقعنا. ستجد مقالات تفصيلية عن البرمجة، والخوارزميات، وأساسيات الإلكترونيات الرقمية التي ستُكمل فهمك لهذا الموضوع. شاركنا في التعليقات تجربتك مع التحويل بين أنظمة العد، أو أي سؤال يدور في ذهنك!
بيان المصداقية والشفافية
تلتزم موسوعة خلية العلمية بأعلى معايير الدقة والمصداقية في تقديم المحتوى العلمي. يستند هذا المقال إلى مصادر أكاديمية موثوقة ومراجع علمية محكّمة.
المصادر المعتمدة: تم الاستشهاد بدراسات من مجلات علمية مرموقة مثل IEEE وACM، بالإضافة إلى معايير دولية من مؤسسات مثل NIST وISO وW3C.
سياسة التحديث: يتم مراجعة المقالات بشكل دوري لضمان مواكبتها لأحدث التطورات في المجال.
تنبيه وإخلاء مسؤولية
المعلومات الواردة في هذا المقال مُقدَّمة لأغراض تعليمية وتثقيفية فقط، ولا تُغني عن الرجوع إلى المصادر الأكاديمية المتخصصة أو استشارة المختصين في مجال علوم الحاسوب والرياضيات.
تسعى موسوعة خلية العلمية جاهدة لتقديم محتوى دقيق ومحدث، إلا أننا لا نضمن خلو المحتوى من الأخطاء أو السهو. يتحمل القارئ مسؤولية التحقق من المعلومات قبل اعتمادها في أي تطبيق عملي أو أكاديمي.
للاطلاع على معلومات أكثر تفصيلاً، يُنصح بمراجعة الكتب الأكاديمية المعتمدة والمصادر الرسمية المذكورة في قسم المراجع.
جرت مراجعة هذا المقال من قبل هيئة التحرير العلمية في موسوعة خلية
آخر تحديث: يناير 2026
لأي استفسار أو ملاحظة، يُرجى التواصل معنا
Scientifically Reviewed Content





