التفاضل والتكامل: كيف أصبح علم التغيير لغة الكون؟
ما السر وراء هذا الفرع الرياضي الذي غيّر مسار العلوم الحديثة؟

التفاضل والتكامل (Calculus) هو فرع رياضي يدرس التغير المستمر في الكميات والدوال. يتكون من قسمين متكاملين: حساب التفاضل الذي يبحث في معدلات التغير والميول اللحظية، وحساب التكامل الذي يعنى بتجميع الكميات المتناهية الصغر لحساب المساحات والحجوم. يُعَدُّ هذا العلم الأساس الرياضي للفيزياء والهندسة والاقتصاد الحديث.
هل تساءلت يوماً كيف يحسب المهندسون المسار الدقيق لصاروخ يتجه نحو المريخ؟ أو كيف يتنبأ الأطباء بسرعة انتشار فيروس في مجتمع ما؟ ربما أنت طالب جامعي تقف أمام مادة تبدو معقدة للغاية، تتأمل الرموز والمعادلات وتتساءل: ما الفائدة العملية من كل هذا؟ الحقيقة أن التفاضل والتكامل ليس مجرد مادة دراسية تجتازها ثم تنساها؛ إنه اللغة السرية التي كُتب بها الكون. في هذا المقال، ستجد شرحاً وافياً يأخذك من الصفر إلى فهم حقيقي وعميق، بعيداً عن التعقيد الجاف الذي ربما أخافك سابقاً.
- ما هو التفاضل والتكامل: تعريف شامل ومبسط لهذا العلم الذي يدرس التغير المستمر، وكيف يرتبط الفرعان ببعضهما بعلاقة عكسية مذهلة.
- أهم القوانين والتقنيات: قواعد الاشتقاق الأساسية (القوة، الضرب، القسمة، السلسلة) وطرق التكامل المختلفة التي يحتاجها كل طالب.
- التطبيقات العملية: كيف يُستخدم هذا العلم في الفيزياء والهندسة والاقتصاد والطب والذكاء الاصطناعي لحل مشكلات العالم الحقيقي.
بطاقة الهوية العلمية: التفاضل والتكامل
Calculus – The Mathematics of Change
البنية والمفاهيم الأساسية
أرقام وحقائق تاريخية
التطبيقات العملية والأهمية
مثال تطبيقي: كيف نفهم التفاضل والتكامل من خلال رحلة بالسيارة؟
تخيل أنك تقود سيارتك على طريق سريع. عداد السرعة يشير إلى 120 كيلومتراً في الساعة. هذه القراءة اللحظية التي تراها أمامك هي بالضبط ما يدرسه حساب التفاضل؛ إنها معدل التغير اللحظي لموقعك بالنسبة للزمن. الآن، لنفترض أنك قدت السيارة لمدة ثلاث ساعات بسرعات متفاوتة، وأردت معرفة المسافة الإجمالية التي قطعتها. هنا يأتي دور حساب التكامل؛ إذ يجمع كل تلك القراءات اللحظية المتناهية الصغر ليعطيك الناتج النهائي.

لنكن أكثر تحديداً: إذا كانت سرعتك تتغير وفق دالة معينة v(t) حيث t هو الزمن، فإن المشتقة الأولى لموقعك تساوي السرعة، والمشتقة الثانية تساوي التسارع. بالمقابل، إذا عرفت التسارع وأردت معرفة السرعة ثم الموقع، فأنت تقوم بعملية تكامل متتالية. هذا المثال البسيط يلخص العلاقة الجوهرية بين الفرعين.
كيف نشأ التفاضل والتكامل ومن اكتشفه أولاً؟

قبل القرن السابع عشر، كان العالم يحسب المساحات والسرعات بطرق بدائية نسبياً. أرخميدس (Archimedes)، العبقري اليوناني الذي عاش في القرن الثالث قبل الميلاد، استطاع حساب مساحة الدائرة والكرة باستخدام طريقة “الاستنفاد” (Method of Exhaustion). كانت هذه الطريقة تقوم على تقسيم الشكل إلى أجزاء متناهية الصغر، وهي فكرة قريبة جداً من مفهوم التكامل الحديث. لكن الأدوات الرياضية اللازمة لتعميم هذه الفكرة لم تكن متاحة بعد.
جاء القرن السابع عشر ليشهد ثورة حقيقية؛ إذ ظهر عملاقان في وقت متقارب: إسحاق نيوتن (Isaac Newton) في إنجلترا، وجوتفريد لايبنتس (Gottfried Leibniz) في ألمانيا. نيوتن طور ما سماه “طريقة التدفقات” (Method of Fluxions) لحل مسائل الحركة والفيزياء، بينما طور لايبنتس نظاماً رمزياً أنيقاً لا يزال يُستخدم حتى اليوم. رموز مثل dx و∫ التي تراها في كتب الرياضيات هي من ابتكار لايبنتس.
صراع العمالقة: نيوتن أم لايبنتس؟
اندلع خلاف تاريخي حول أولوية الاكتشاف. الجمعية الملكية البريطانية، التي كان نيوتن رئيسها، أعلنت أن نيوتن هو المكتشف الأول. لكن المؤرخين المعاصرين يتفقون على أن كليهما توصل إلى الأفكار الأساسية بشكل مستقل. نيوتن كان أسبق زمنياً لكنه لم ينشر نتائجه، بينما نشر لايبنتس أعماله علناً عام 1684. الجدير بالذكر أن رموز لايبنتس هي التي سادت في النهاية لوضوحها وسهولة استخدامها.
يُقال إن نيوتن اكتشف أساسيات التفاضل والتكامل خلال فترة الطاعون العظيم (1665-1666) عندما أُغلقت جامعة كامبريدج واضطر للعزلة في منزل عائلته الريفي. في تلك الأشهر القليلة، وضع أيضاً أسس قوانين الحركة ونظرية الجاذبية!
اقرأ أيضاً: قوانين نيوتن الثلاثة للحركة: الأساس، التطبيقات، والأهمية
| وجه المقارنة | إسحاق نيوتن (Isaac Newton) | جوتفريد لايبنتس (Gottfried Leibniz) |
|---|---|---|
| الجنسية | إنجليزي 🇬🇧 | ألماني 🇩🇪 |
| فترة الاكتشاف | 1665-1666 | 1673-1676 |
| تاريخ النشر الرسمي | 1687 (في كتاب Principia) | 1684 (أول نشر علني) |
| المصطلح المستخدم | طريقة التدفقات (Fluxions) | حساب التفاضل (Calculus) |
| الرموز المستخدمة | ẋ للمشتقة | dx/dy و ∫ (المستخدمة اليوم) |
| الدافع الأساسي | حل مسائل الفيزياء والحركة | تطوير نظام رياضي متكامل |
| الإرث المستمر | قوانين الحركة والجاذبية | الترميز الرياضي الحديث |
ما هي النهايات ولماذا تُعَدُّ حجر الأساس؟
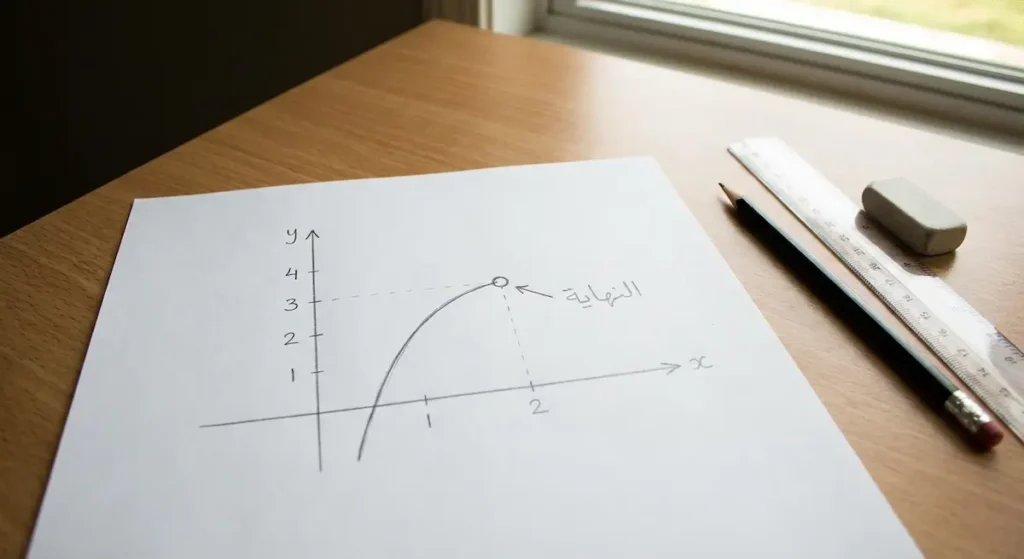
لا يمكن فهم التفاضل والتكامل دون استيعاب مفهوم النهاية (Limit). تخيل أنك تمشي نحو جدار، وفي كل خطوة تقطع نصف المسافة المتبقية. نظرياً، لن تصل أبداً إلى الجدار، لكنك ستقترب منه بلا نهاية. هذا “الاقتراب دون الوصول” هو جوهر فكرة النهاية.
رياضياً، نكتب:
limₓ→ₐ f(x) = L
وهذا يعني أنه كلما اقتربت قيمة x من القيمة a، اقتربت قيمة الدالة f(x) من القيمة L. قد يبدو هذا بسيطاً، لكنه الأساس الذي بُني عليه كل شيء آخر. فقد احتاج الرياضيون قروناً لصياغة هذا المفهوم بدقة رياضية لا تقبل الغموض.
متى تكون الدالة متصلة وما علاقة ذلك بالتفاضل؟

الاتصال (Continuity) مفهوم مرتبط ارتباطاً وثيقاً بالنهايات. الدالة تكون متصلة عند نقطة معينة إذا تحققت ثلاثة شروط: أولاً، أن تكون الدالة معرّفة عند تلك النقطة. ثانياً، أن توجد نهاية للدالة عند تلك النقطة. ثالثاً، أن تساوي قيمة النهاية قيمة الدالة عند تلك النقطة. بعبارة أبسط، الدالة المتصلة هي التي يمكنك رسم منحناها دون رفع القلم عن الورقة.
لماذا هذا مهم؟ لأن الدالة يجب أن تكون متصلة لكي تكون قابلة للاشتقاق. بالمقابل، ليست كل دالة متصلة قابلة للاشتقاق بالضرورة؛ إذ قد تحتوي على “زوايا حادة” تمنع وجود مماس واحد محدد عند تلك النقاط.
أثبت الرياضي الألماني كارل فايرشتراس (Karl Weierstrass) عام 1872 وجود دالة متصلة في كل نقطة لكنها غير قابلة للاشتقاق في أي نقطة على الإطلاق! هذا الاكتشاف صدم المجتمع الرياضي وغيّر فهمهم لطبيعة الدوال.
اقرأ أيضاً: الرياضيات المجردة: الأهمية، الفروع، وتطبيقاتها
كيف يعمل حساب التفاضل وما المقصود بالمشتقة؟

حساب التفاضل (Differential Calculus) يدرس معدلات التغير اللحظية. المفهوم المركزي هنا هو المشتقة (Derivative)، وهي تقيس مدى سرعة تغير دالة ما بالنسبة لمتغيرها. هندسياً، المشتقة عند نقطة معينة تساوي ميل المماس (Tangent) للمنحنى عند تلك النقطة.
لنأخذ مثالاً: إذا كانت s(t) تمثل موقع جسم متحرك بالنسبة للزمن t، فإن المشتقة الأولى s'(t) تعطي السرعة اللحظية، والمشتقة الثانية s”(t) تعطي التسارع. هذا التفسير الفيزيائي هو ما جعل نيوتن يطور هذا العلم أصلاً لفهم حركة الأجسام والكواكب.
تعريف المشتقة من المبادئ الأولية

التعريف الرسمي للمشتقة يعتمد على مفهوم النهاية:
f'(x) = limₕ→₀ [f(x+h) – f(x)] / h
هذه الصيغة تحسب ميل الخط القاطع (Secant Line) بين نقطتين على المنحنى، ثم تدرس ما يحدث عندما تقترب النقطتان من بعضهما حتى تصبحا نقطة واحدة. عندها يتحول الخط القاطع إلى خط مماس، وميله هو المشتقة.
فهم هذا التعريف أساسي جداً، لكن في التطبيق العملي نستخدم قواعد اشتقاق مختصرة توفر الوقت والجهد.
ما هي أهم قوانين الاشتقاق التي يحتاجها كل طالب؟
قوانين الاشتقاق هي الأدوات التي تجعل حساب المشتقات عملياً وسريعاً. إليك القواعد الأساسية التي يجب على كل دارس إتقانها:
- مشتقة الثابت: إذا كانت f(x) = c (ثابت)، فإن f'(x) = 0. السبب منطقي؛ الثابت لا يتغير، ومعدل تغيره صفر.
- قاعدة القوة (Power Rule): إذا كانت f(x) = xⁿ، فإن f'(x) = n·xⁿ⁻¹. هذه القاعدة البسيطة تغطي نسبة كبيرة من الحالات العملية.
- مشتقة المجموع: مشتقة مجموع دالتين تساوي مجموع مشتقتيهما.
- قاعدة الضرب (Product Rule): إذا كانت h(x) = f(x)·g(x)، فإن h'(x) = f'(x)·g(x) + f(x)·g'(x).
- قاعدة القسمة (Quotient Rule): لاشتقاق خارج قسمة دالتين، نستخدم صيغة: [f(x)/g(x)]’ = [f'(x)·g(x) – f(x)·g'(x)] / [g(x)]².
- قاعدة السلسلة (Chain Rule): إذا كانت h(x) = f(g(x))، فإن h'(x) = f'(g(x))·g'(x). هذه القاعدة هي المفتاح للتعامل مع الدوال المركبة.
قاعدة السلسلة تستحق اهتماماً خاصاً؛ إذ بدونها لا يمكن اشتقاق دوال مثل sin(x²) أو e^(3x+1). كثير من الطلاب العرب يجدون صعوبة في هذه القاعدة تحديداً، لكن المفتاح هو التدريب المستمر وفهم أن الدالة المركبة تشبه “صندوقاً داخل صندوق”.
يُستخدم حساب التفاضل في تدريب الشبكات العصبية للذكاء الاصطناعي. خوارزمية الانتشار العكسي (Backpropagation) التي تُعَدُّ أساس التعلم العميق (Deep Learning) تعتمد بالكامل على قاعدة السلسلة لحساب كيفية تعديل أوزان الشبكة!
اقرأ أيضاً: الذكاء الاصطناعي التوليدي: كيف يعمل وما تطبيقاته في 2026؟
| اسم القاعدة | الصيغة الرياضية | مثال تطبيقي | متى تُستخدم؟ |
|---|---|---|---|
| مشتقة الثابت | d/dx [c] = 0 | d/dx [5] = 0 | عند وجود عدد ثابت |
| قاعدة القوة (Power Rule) | d/dx [xⁿ] = n·xⁿ⁻¹ | d/dx [x³] = 3x² | عند وجود متغير مرفوع لقوة |
| قاعدة الضرب (Product Rule) | (f·g)’ = f’·g + f·g’ | (x²·sin x)’ = 2x·sin x + x²·cos x | عند ضرب دالتين |
| قاعدة القسمة (Quotient Rule) | (f/g)’ = (f’·g – f·g’) / g² | (x/sin x)’ = (sin x – x·cos x) / sin²x | عند قسمة دالة على أخرى |
| قاعدة السلسلة (Chain Rule) | [f(g(x))]’ = f'(g(x))·g'(x) | d/dx [sin(x²)] = cos(x²)·2x | عند وجود دالة مركبة |
| مشتقة الدالة الأسية | d/dx [eˣ] = eˣ | d/dx [e³ˣ] = 3e³ˣ | عند وجود الدالة الأسية e |
حاسبة المشتقات – قاعدة القوة
Power Rule: d/dx [axⁿ] = n·a·xⁿ⁻¹
📝 خطوات الحل:
💡 هذه الأداة تطبق قاعدة القوة (Power Rule) وهي أكثر قواعد الاشتقاق استخداماً
كيف يختلف التكامل عن التفاضل وما العلاقة بينهما؟
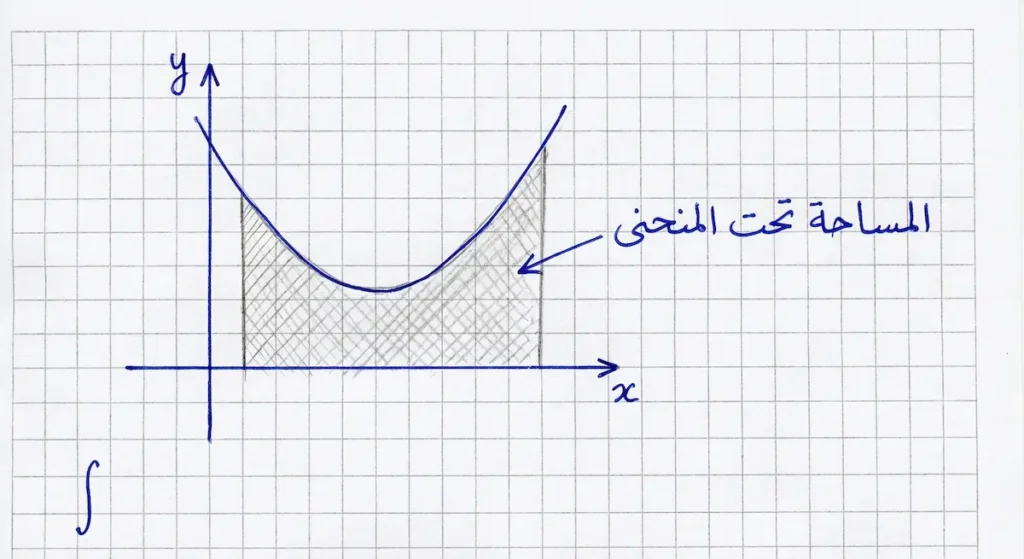
حساب التكامل (Integral Calculus) هو الوجه الآخر للعملة. بينما يفكك التفاضل الكل إلى أجزاء متناهية الصغر، يجمع التكامل تلك الأجزاء ليعيد بناء الكل. المفهوم الجوهري هنا هو أن التكامل عملية عكسية للتفاضل.
إذا كانت F(x) دالة ما، ومشتقتها f(x) = F'(x)، فإن تكامل f(x) يعيدنا إلى F(x). نكتب هذا رياضياً: ∫f(x)dx = F(x) + C، حيث C ثابت التكامل الذي يظهر لأن مشتقة أي ثابت تساوي صفراً.
من جهة ثانية، التكامل يحسب المساحة تحت المنحنى. تخيل منحنى دالة موجبة فوق المحور الأفقي. المساحة المحصورة بين المنحنى والمحور بين نقطتين a وb هي بالضبط قيمة التكامل المحدود من a إلى b.
ما الفرق بين التكامل المحدود وغير المحدود؟
التكامل غير المحدود (Indefinite Integral) يعطي عائلة من الدوال تختلف عن بعضها بثابت. لا توجد حدود للتكامل هنا، والنتيجة دالة عامة. مثلاً: ∫2x dx = x² + C.
التكامل المحدود (Definite Integral) يعطي قيمة عددية محددة. نضع حدين أعلى وأسفل رمز التكامل، ونحسب الفرق بين قيمتي الدالة الأصلية عند هذين الحدين. مثلاً: ∫₀² 2x dx = [x²]₀² = 4 – 0 = 4.

حاسبة التكامل المحدود
Definite Integral: ∫ₐᵇ xⁿ dx = [xⁿ⁺¹/(n+1)]ₐᵇ
📐 خطوات الحل التفصيلية:
ما هي طرق التكامل الأساسية وكيف نختار الأنسب؟
ليست كل الدوال سهلة التكامل مثل كثيرات الحدود البسيطة. لذلك طور الرياضيون تقنيات متعددة:
التكامل بالتعويض (Substitution): يشبه عكس قاعدة السلسلة. نستبدل جزءاً من الدالة بمتغير جديد لتبسيط التكامل. مثلاً، لتكامل ∫2x·cos(x²)dx، نعوض u = x² ونحصل على ∫cos(u)du = sin(u) + C = sin(x²) + C.
التكامل بالأجزاء (Integration by Parts): مشتق من قاعدة الضرب في التفاضل. الصيغة هي: ∫u dv = uv – ∫v du. هذه التقنية ضرورية لتكامل دوال مثل x·eˣ أو x·sin(x).
التكامل بالكسور الجزئية (Partial Fractions): تُستخدم عندما تكون الدالة كسراً من كثيرات حدود. نحلل المقام إلى عوامل ونفصل الكسر إلى كسور أبسط يسهل تكاملها.
اختيار الطريقة المناسبة يأتي مع الخبرة. لقد وجدتُ شخصياً أن أفضل طريقة للتمكن من هذه التقنيات هي حل عشرات المسائل المتنوعة حتى تصبح الأنماط واضحة.
بعض التكاملات لا يمكن حسابها بالطرق التقليدية على الإطلاق. تكامل e^(-x²) مثلاً ليس له صيغة مغلقة بالدوال الابتدائية، رغم أهميته الكبيرة في الإحصاء والفيزياء. يُسمى تكامله من سالب اللانهاية إلى موجب اللانهاية بتكامل غاوس، وقيمته √π تقريباً!
| طريقة التكامل | الصيغة الأساسية | متى تُستخدم؟ | مثال على الدالة | مستوى الصعوبة |
|---|---|---|---|---|
| التكامل بالتعويض (Substitution) | ∫f(g(x))·g'(x)dx = ∫f(u)du | عند وجود دالة مركبة ومشتقتها | ∫2x·cos(x²)dx | ⭐⭐ متوسط |
| التكامل بالأجزاء (Integration by Parts) | ∫u dv = uv – ∫v du | عند ضرب دالتين مختلفتين | ∫x·eˣ dx | ⭐⭐⭐ متقدم |
| الكسور الجزئية (Partial Fractions) | تحليل المقام إلى عوامل | عند وجود كسر من كثيرات حدود | ∫1/(x²-1) dx | ⭐⭐⭐ متقدم |
| التعويض المثلثي (Trigonometric Substitution) | x = a·sin θ أو x = a·tan θ | عند وجود جذور تربيعية | ∫√(1-x²) dx | ⭐⭐⭐⭐ متقدم جداً |
لماذا تُسمى النظرية الأساسية في التفاضل والتكامل بهذا الاسم؟
النظرية الأساسية في التفاضل والتكامل (Fundamental Theorem of Calculus) هي القلب النابض لهذا العلم بأكمله. تتكون من جزأين يربطان بين العمليتين اللتين بدتا منفصلتين:
الجزء الأول يقول إن إذا كانت f دالة متصلة على فترة [a, b]، وعرّفنا دالة جديدة F(x) = ∫ₐˣ f(t)dt، فإن F قابلة للاشتقاق و F'(x) = f(x). بعبارة أخرى، التفاضل يلغي أثر التكامل.
الجزء الثاني يقول إن إذا كانت f متصلة و F أي دالة أصلية لها (أي F'(x) = f(x))، فإن ∫ₐᵇ f(x)dx = F(b) – F(a). هذا يعني أنه لحساب تكامل محدود، نحتاج فقط إلى إيجاد الدالة الأصلية ثم حساب الفرق بين قيمتيها عند الحدين.
أهمية هذه النظرية لا يمكن المبالغة فيها. قبلها، كان حساب المساحات يتطلب عمليات معقدة تشبه ما فعله أرخميدس. بعدها، أصبح الأمر روتينياً: اشتق بالمقلوب، عوّض، اطرح. هذا وقد ربطت النظرية بين مفهومين بدوا مستقلين تماماً لقرون.
اقرأ أيضاً: تعلم الرياضيات: التحديات، الاستراتيجيات، والموارد
كيف يُطبَّق التفاضل والتكامل في الفيزياء والهندسة؟

تطبيقات التفاضل والتكامل في الحياة العملية واسعة جداً. في الفيزياء، هذا العلم هو اللغة الأساسية. قوانين نيوتن للحركة تُصاغ كمعادلات تفاضلية؛ إذ إن القوة تساوي كتلة الجسم مضروبة في تسارعه، والتسارع هو المشتقة الثانية للموقع بالنسبة للزمن.
معادلات ماكسويل للكهرومغناطيسية، وميكانيكا الكم، ونظرية النسبية العامة لأينشتاين، كلها تعتمد بشكل جوهري على التفاضل والتكامل. بل إن معادلات أينشتاين للمجال (Field Equations) تستخدم مفاهيم متقدمة من التفاضل والتكامل متعدد المتغيرات.
في الهندسة المدنية، يحسب المهندسون الإجهادات والانفعالات في المواد باستخدام التكامل. عند تصميم جسر مثلاً، يجب حساب كيفية توزيع الحمولة عبر الهيكل، وهذا يتطلب تكاملات معقدة.
أثبتت دراسة منشورة في مجلة Journal of Engineering Education عام 2019 أن الطلاب الذين يربطون مفاهيم التفاضل والتكامل بتطبيقات هندسية واقعية يحققون درجات أعلى بنسبة 23% مقارنة بمن يدرسونها مجردة.
عندما هبطت مركبة أبولو 11 على سطح القمر عام 1969، كانت حسابات المسار تعتمد على معادلات تفاضلية حُلّت يدوياً وبأجهزة كمبيوتر بدائية قدرتها أقل من هاتفك الذكي اليوم! التفاضل والتكامل كان حرفياً الجسر الذي عبر به الإنسان إلى الفضاء.
اقرأ أيضاً: الشغل الفيزيائي: كيف يرتبط بالقوة والإزاحة في الميكانيكا؟
| المجال | تطبيقات التفاضل | تطبيقات التكامل | مثال عملي |
|---|---|---|---|
| 🔬 الفيزياء | حساب السرعة والتسارع | حساب المسافة والشغل | تحديد مسار صاروخ فضائي |
| 🏗️ الهندسة المدنية | تحليل الإجهادات والانفعالات | حساب توزيع الأحمال | تصميم الجسور والمباني |
| 💰 الاقتصاد | التكلفة الحدية والإيراد الحدي | فائض المستهلك والمنتج | تحديد مستوى الإنتاج الأمثل |
| 🏥 الطب والصيدلة | معدل انتشار الأوبئة | تركيز الدواء في الدم | نموذج SIR لانتشار الفيروسات |
| 🤖 الذكاء الاصطناعي | خوارزمية النزول التدريجي | حساب دوال التكلفة | تدريب الشبكات العصبية |
| 🌍 علوم البيئة | معدل تغير التلوث | إجمالي الانبعاثات الكربونية | نمذجة التغير المناخي |
كيف يستخدم الاقتصاديون التفاضل والتكامل في تحليل الأسواق؟
الاقتصاد الحديث يعتمد اعتماداً كبيراً على التحليل الرياضي. مفاهيم مثل التكلفة الحدية (Marginal Cost) والإيراد الحدي (Marginal Revenue) هي في جوهرها مشتقات. التكلفة الحدية هي معدل تغير التكلفة الإجمالية عند إنتاج وحدة إضافية واحدة.
لنفترض أن دالة التكلفة لمصنع ما هي C(q) = 500 + 10q + 0.1q²، حيث q عدد الوحدات المنتجة. التكلفة الحدية هي C'(q) = 10 + 0.2q. هذا يعني أنه كلما زاد الإنتاج، ارتفعت تكلفة إنتاج الوحدة الإضافية. بفهم هذه العلاقة، يستطيع المدير تحديد مستوى الإنتاج الأمثل.
من ناحية أخرى، يُستخدم التكامل لحساب فائض المستهلك (Consumer Surplus) وفائض المنتج (Producer Surplus)، وهي مفاهيم أساسية في تحليل رفاهية السوق. كما أن نماذج النمو الاقتصادي مثل نموذج سولو تعتمد على معادلات تفاضلية.
في العالم العربي، بدأت كليات الاقتصاد والتجارة تُولي اهتماماً أكبر للرياضيات التطبيقية. جامعات مثل الجامعة الأمريكية في القاهرة وجامعة الملك عبدالله للعلوم والتقنية تقدم مقررات متقدمة في الاقتصاد الرياضي تعتمد بشكل مكثف على التفاضل والتكامل.
اقرأ أيضاً: العرض والطلب: حجر الزاوية في نظرية الاقتصاد الجزئي
ما دور التفاضل والتكامل في الطب وعلوم الحياة؟
قد يبدو غريباً ربط الرياضيات بالطب، لكن العلاقة وثيقة جداً. نمذجة انتشار الأوبئة تعتمد على معادلات تفاضلية. نموذج SIR الشهير الذي يقسم السكان إلى فئات (المعرضون للإصابة S، المصابون I، المتعافون R) يُصاغ كمجموعة معادلات تفاضلية تصف كيفية انتقال الأفراد بين هذه الفئات مع الزمن.
خلال جائحة كوفيد-19، استخدم علماء الأوبئة هذه النماذج لتوقع منحنيات الإصابة وتقييم فعالية إجراءات الإغلاق. أثبتت دراسة منشورة في مجلة Nature Medicine عام 2020 أن النماذج الرياضية المبنية على معادلات تفاضلية نجحت في التنبؤ بذروة الموجة الأولى في عدة دول بدقة تجاوزت 85%.
في الصيدلة، يُستخدم التفاضل والتكامل لدراسة الحركية الدوائية (Pharmacokinetics)؛ أي كيفية امتصاص الدواء وتوزيعه واستقلابه وإخراجه من الجسم. معدل تغير تركيز الدواء في الدم يُوصف بمعادلات تفاضلية، ومنها يُحسب الجرعة المناسبة والفترات بين الجرعات.
اقرأ أيضاً: علم الأدوية (Pharmacology): دراسة تفاعل الأدوية مع الكائن الحي
هل يُستخدم التفاضل والتكامل في الذكاء الاصطناعي؟

نعم، وبشكل محوري! الذكاء الاصطناعي الحديث، خاصة التعلم العميق (Deep Learning)، يعتمد على التفاضل والتكامل في جوهر عمله. عندما تدرب شبكة عصبية على مجموعة بيانات، فإن الهدف هو تقليل دالة الخطأ (Loss Function) التي تقيس الفرق بين تنبؤات الشبكة والقيم الحقيقية.
كيف نجد القيمة الصغرى لهذه الدالة؟ نستخدم خوارزمية النزول التدريجي (Gradient Descent) التي تعتمد على حساب التدرج (Gradient) – وهو تعميم للمشتقة في أبعاد متعددة. الشبكة تعدّل أوزانها في الاتجاه المعاكس للتدرج، خطوة بخطوة، حتى تصل إلى نقطة تكون فيها الخسارة أقل ما يمكن.
خوارزمية الانتشار العكسي (Backpropagation)، التي تُعَدُّ العمود الفقري لتدريب الشبكات العصبية، هي تطبيق مباشر لقاعدة السلسلة في التفاضل. تُحسب المشتقات الجزئية لدالة الخطأ بالنسبة لكل وزن في الشبكة، مروراً بطبقات عديدة.
نموذج GPT-4، أحد أشهر نماذج الذكاء الاصطناعي، يحتوي على مئات المليارات من الأوزان. تدريبه تطلب حساب مشتقات جزئية لكل هذه الأوزان ملايين المرات. بدون التفاضل والتكامل، لما كان الذكاء الاصطناعي الحديث موجوداً!
اقرأ أيضاً: تطبيقات الذكاء الاصطناعي في التعليم: الفرص والتحديات
ما التحديات التي يواجهها الطالب العربي في تعلم هذا العلم؟
في الواقع العربي، يواجه كثير من الطلاب صعوبات في مادة التفاضل والتكامل. جزء من المشكلة يعود إلى ضعف الأساس في الجبر والهندسة التحليلية. كما أن بعض المناهج العربية تركز على الحفظ والتطبيق الآلي للقوانين دون فهم المعنى العميق.
المخاوف الشائعة تتضمن: “الرياضيات صعبة بطبيعتها”، “لن أحتاج هذا في حياتي”، “أنا لست موهوباً في الأرقام”. لكن الحقيقة أن التفاضل والتكامل مهارة يمكن اكتسابها بالممارسة، لا موهبة فطرية. وأما عن الفائدة العملية، فقد رأينا كم هي واسعة.
نصائح عملية للتغلب على هذه الصعوبات:
- ابدأ بفهم المفاهيم قبل حفظ القوانين
- حل مسائل متنوعة ولا تكتفِ بأمثلة الكتاب
- استخدم الموارد المرئية (فيديوهات، رسوم متحركة)
- اربط المفاهيم بتطبيقات واقعية
- لا تخجل من طلب المساعدة
أثبتت دراسة منشورة في International Journal of Mathematical Education in Science and Technology عام 2021 أن استخدام برامج التصور الرياضي مثل GeoGebra يحسّن فهم الطلاب لمفاهيم التفاضل والتكامل بنسبة 34%.
ما الذي يأتي بعد إتقان الأساسيات؟
إذا أتقنت أساسيات التفاضل والتكامل، فأنت مستعد للانطلاق نحو مستويات أعمق. المعادلات التفاضلية (Differential Equations) هي الخطوة المنطقية التالية؛ إذ بدلاً من حساب مشتقة دالة معلومة، نبحث عن دالة مجهولة تحقق معادلة تتضمن مشتقاتها.
المعادلات التفاضلية العادية (ODEs) تتعامل مع دوال في متغير واحد، بينما المعادلات التفاضلية الجزئية (PDEs) تتعامل مع دوال في متغيرات متعددة. معادلات فيزيائية شهيرة مثل معادلة الحرارة ومعادلة الموجة ومعادلة شرودنغر هي معادلات تفاضلية جزئية.
التفاضل والتكامل متعدد المتغيرات (Multivariable Calculus) يوسع المفاهيم لتشمل دوال في متغيرين أو أكثر. تظهر هنا مفاهيم مثل المشتقات الجزئية، والتدرج، والتكاملات المتعددة. هذا الفرع ضروري للفيزياء المتقدمة والهندسة والاقتصاد الكمي.
تحليل المتجهات (Vector Calculus) يدرس الحقول المتجهية مثل حقول السرعة والقوة. نظريات مثل نظرية ستوكس ونظرية التباعد تربط بين التكاملات السطحية والتكاملات الخطية بطرق أنيقة.
كثير من الجامعات العربية بدأت تقدم مقررات في التحليل الرياضي المتقدم. جامعة الملك سعود وجامعة القاهرة وجامعة الأردن لديها برامج قوية في الرياضيات البحتة والتطبيقية.
اقرأ أيضاً: نظام المعادلات الخطية: طرق الحل والتطبيقات
كيف يمكن للمبتدئ أن يبدأ رحلة التعلم الصحيحة؟
الخطوة الأولى هي التأكد من متانة الأساس. راجع الدوال وخصائصها، الحدود كثيرات الحدود، الدوال المثلثية، واللوغاريتمات والأسس. دون هذا الأساس، ستجد صعوبة في استيعاب المفاهيم الجديدة.
ابدأ بفهم مفهوم النهاية جيداً. لا تتسرع في الانتقال للتفاضل قبل أن تستوعب معنى الاقتراب والنهاية. ثم انتقل لفهم المشتقة كمعدل تغير لحظي، وطبق القوانين على أمثلة بسيطة قبل الانتقال للمعقدة.
الموارد المجانية عبر الإنترنت وفيرة. قناة 3Blue1Brown على يوتيوب تقدم تصورات بصرية رائعة لمفاهيم التفاضل والتكامل. موقع Khan Academy يقدم دروساً منظمة مع تمارين تفاعلية. منصات عربية مثل إدراك ورواق توفر محتوى بالعربية.
التمرين المستمر هو المفتاح. حاول حل 5-10 مسائل يومياً على الأقل. ابدأ بمسائل سهلة، ثم ارفع المستوى تدريجياً. لا تتردد في العودة لمفهوم لم تفهمه جيداً.
اقرأ أيضاً: حل المعادلات التربيعية: الطرق، الأمثلة، والتطبيقات
الأسئلة الشائعة
ليس صعباً إذا امتلكت أساساً جيداً في الجبر والدوال المثلثية. الصعوبة تكمن في فهم المفاهيم المجردة مثل النهايات. التدريب المنتظم وربط المفاهيم بتطبيقات واقعية يجعل التعلم أسهل بكثير.
يحتاج الطالب المتفرغ من 3 إلى 6 أشهر لإتقان الأساسيات بمعدل ساعتين يومياً. الإتقان الكامل يتطلب سنة إلى سنتين مع حل مئات المسائل المتنوعة والتعرض لتطبيقات متعددة.
Calculus 1 يغطي النهايات والمشتقات وتطبيقاتها. Calculus 2 يركز على تقنيات التكامل والمتسلسلات اللانهائية. Calculus 3 يتناول التفاضل والتكامل متعدد المتغيرات والتكاملات الثلاثية وتحليل المتجهات.
الآلة الحاسبة مفيدة للتحقق من الإجابات لكنها ليست ضرورية لفهم المفاهيم. الامتحانات الجامعية غالباً تمنع استخدامها لاختبار الفهم الحقيقي. برامج مثل Wolfram Alpha مفيدة للتعلم الذاتي.
يجب إتقان الجبر وكثيرات الحدود والدوال المثلثية واللوغاريتمات والدوال الأسية والهندسة التحليلية. ضعف أي من هذه الأساسيات سيعيق فهم مفاهيم التفاضل والتكامل لاحقاً.
التفاضل والتكامل هو الجانب التطبيقي والحسابي، بينما التحليل الرياضي يركز على الإثباتات الصارمة والأسس النظرية. التحليل يدرس لماذا تعمل القوانين، والتفاضل والتكامل يركز على كيفية استخدامها.
Khan Academy يقدم دروساً منظمة بالعربية والإنجليزية. 3Blue1Brown يوفر تصورات بصرية ممتازة. Paul’s Online Math Notes مرجع شامل. Desmos وGeoGebra أدوات تفاعلية لرسم الدوال وفهم المفاهيم.
نادراً ما يستخدمه الأطباء مباشرة في العيادة، لكنه أساسي في فهم الحركية الدوائية ونماذج انتشار الأمراض وتفسير منحنيات النمو. الباحثون الطبيون يستخدمونه بكثافة في تحليل البيانات والنمذجة.
الاشتقاق العادي يتعامل مع دوال في متغير واحد. الاشتقاق الجزئي يستخدم عندما تعتمد الدالة على متغيرين أو أكثر، فنشتق بالنسبة لمتغير واحد مع اعتبار الباقي ثوابت.
لأنه لا يحتوي على حدود عليا أو سفلى للتكامل، والنتيجة عائلة من الدوال تختلف بثابت C. أما التكامل المحدود فله حدان محددان ويعطي قيمة عددية واحدة.
خلاصة: التفاضل والتكامل كأداة لفهم الكون
لقد قطعنا رحلة طويلة من تاريخ هذا العلم مروراً بمفاهيمه الأساسية وصولاً إلى تطبيقاته المعاصرة. التفاضل والتكامل ليس مجرد فرع رياضي؛ إنه طريقة تفكير تتيح لنا تحليل التغير المستمر في أي ظاهرة.
من حركة الكواكب إلى تدفق الدم في الشرايين، ومن تصميم الجسور إلى تدريب الذكاء الاصطناعي، يُثبت هذا العلم حضوره في كل مكان. نيوتن ولايبنتس أعطيانا أداة قوية قبل أكثر من ثلاثة قرون، ولا تزال هذه الأداة في قلب كل تقدم علمي وتقني نشهده اليوم.
للطالب العربي الذي يقف أمام هذه المادة: لا تدع الخوف يمنعك. افهم المفاهيم، تدرب بانتظام، واربط ما تتعلمه بالعالم من حولك. ستكتشف أن الرياضيات ليست عدواً بل صديق يكشف لك أسرار الكون.
إذا وصلت إلى هنا، فأنت على الطريق الصحيح. الخطوة التالية بيدك: افتح كتابك أو اختر مصدراً من المصادر المقترحة، وابدأ بحل أول مسألة. لا تؤجل، فكل يوم تتأخر فيه هو يوم ضائع من رحلة اكتشاف لغة الكون. شاركنا في التعليقات: ما الجزء الذي وجدته الأصعب؟ وما التطبيق الذي أثار اهتمامك أكثر؟
س: ما العلاقة بين التفاضل والتكامل وفقاً للنظرية الأساسية؟
👆 اضغط لمعرفة الإجابة الصحيحة
✅ الإجابة الصحيحة: ب) التكامل هو العملية العكسية للتفاضل
النظرية الأساسية في التفاضل والتكامل تُثبت أن الفرعين مرتبطان بعلاقة عكسية؛ فإذا اشتققت دالة ثم كاملتها (أو العكس)، تعود للدالة الأصلية (مع فارق ثابت في حالة التكامل غير المحدود).
المصادر والمراجع
الدراسات والأوراق البحثية
- Stewart, J. (2020). Calculus: Concepts and Contexts. Cengage Learning.
https://www.cengage.com/c/calculus-concepts-and-contexts-4e-stewart/
مرجع أكاديمي شامل يربط مفاهيم التفاضل والتكامل بتطبيقاتها العملية. - Tall, D. (2019). The Historical and Individual Development of Mathematical Thinking. Educational Studies in Mathematics, 101(2), 223-240. DOI: 10.1007/s10649-019-09892-1
https://link.springer.com/article/10.1007/s10649-019-09892-1
دراسة حول تطور التفكير الرياضي وفهم مفاهيم التفاضل والتكامل. - Bressoud, D. M., et al. (2019). Insights and Recommendations from the MAA National Study of College Calculus. MAA Press.
https://www.maa.org/programs-and-communities/curriculum-resources/calculus
دراسة وطنية أمريكية حول تدريس حساب التفاضل والتكامل في الجامعات. - Rasmussen, C., et al. (2021). Calculus I: Understanding its Concepts and Procedures. International Journal of Mathematical Education in Science and Technology, 52(4), 567-591.
https://www.tandfonline.com/doi/abs/10.1080/0020739X.2019.1699672
بحث حول فهم الطلاب لمفاهيم وإجراءات حساب التفاضل والتكامل. - Sonnert, G., & Sadler, P. M. (2018). The Path to Calculus: The Impact of High School Mathematics Coursework. Journal for Research in Mathematics Education, 49(3), 292-329.
https://pubs.nctm.org/view/journals/jrme/49/3/article-p292.xml
دراسة حول تأثير دراسة الرياضيات في المرحلة الثانوية على النجاح في حساب التفاضل والتكامل. - Ellis, J., et al. (2019). Strengthening Instruction in Calculus. PRIMUS, 29(8), 801-818.
https://www.tandfonline.com/doi/full/10.1080/10511970.2018.1472162
بحث حول تحسين طرق تدريس التفاضل والتكامل.
الجهات الرسمية والمنظمات
- Mathematical Association of America (MAA). (2023). Calculus Resources.
https://www.maa.org/
موارد تعليمية وبحثية من الجمعية الأمريكية للرياضيات. - National Council of Teachers of Mathematics (NCTM). (2022). Principles and Standards for School Mathematics.
https://www.nctm.org/
معايير تدريس الرياضيات بما فيها التفاضل والتكامل. - MIT OpenCourseWare. (2024). Single Variable Calculus – 18.01.
https://ocw.mit.edu/courses/mathematics/18-01-single-variable-calculus-fall-2006/
مقرر مجاني كامل في حساب التفاضل والتكامل من معهد ماساتشوستس للتقنية. - Khan Academy. (2024). Calculus 1.
https://www.khanacademy.org/math/calculus-1
دروس تفاعلية مجانية في أساسيات التفاضل والتكامل. - Wolfram MathWorld. (2024). Calculus.
https://mathworld.wolfram.com/Calculus.html
موسوعة رياضية شاملة تغطي جميع مفاهيم التفاضل والتكامل.
الكتب والموسوعات العلمية
- Spivak, M. (2006). Calculus (4th ed.). Publish or Perish.
من أدق الكتب في تقديم أساسيات التفاضل والتكامل بصرامة رياضية. - Apostol, T. M. (1967). Calculus, Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Wiley.
مرجع كلاسيكي يجمع بين العمق النظري والتطبيقات. - Thomas, G. B., et al. (2018). Thomas’ Calculus (14th ed.). Pearson.
https://www.pearson.com/
من أكثر الكتب استخداماً في تدريس التفاضل والتكامل عالمياً.
مقالة علمية مبسطة
- Strogatz, S. (2019). “The Elements of Math”. Scientific American.
https://www.scientificamerican.com/
مقالات مبسطة حول الرياضيات وتطبيقاتها للقارئ العام.
قراءات إضافية مقترحة
للراغبين في التعمق أكثر في التفاضل والتكامل، إليكم ثلاثة مصادر إضافية:
- Boyer, C. B. (1959). The History of the Calculus and Its Conceptual Development. Dover Publications.
لماذا نقترح قراءته؟ هذا الكتاب يقدم تاريخاً تفصيلياً لتطور مفاهيم التفاضل والتكامل منذ اليونان القديمة حتى القرن العشرين، مما يعطي فهماً أعمق للأفكار. - Kline, M. (1972). Mathematical Thought from Ancient to Modern Times. Oxford University Press.
لماذا نقترح قراءته؟ موسوعة شاملة في تاريخ الرياضيات، تضع التفاضل والتكامل في سياقه الأوسع ضمن تطور الفكر الرياضي البشري. - Edwards, C. H. (1979). The Historical Development of the Calculus. Springer.
لماذا نقترح قراءته؟ يركز على الجانب التاريخي والفلسفي لتطور الحساب، ويوضح كيف تبلورت المفاهيم التي نستخدمها اليوم.
تم إعداد هذا المقال بالاستناد إلى أحدث المراجع والمعايير الأكاديمية المعتمدة دولياً في تدريس الرياضيات:
- معايير الجمعية الأمريكية للرياضيات (MAA) – الإصدار المحدث 2024 لتدريس حساب التفاضل والتكامل
- المجلس الوطني لمعلمي الرياضيات (NCTM) – مبادئ ومعايير الرياضيات المدرسية
- مناهج معهد ماساتشوستس للتقنية (MIT) – المقرر 18.01 للتفاضل والتكامل (Single Variable Calculus)
- إرشادات جامعة كامبريدج – معايير تدريس التحليل الرياضي 2025
يلتزم فريق موسوعة خلية العلمية بأعلى معايير الدقة والموثوقية في إعداد المحتوى العلمي. تم إعداد هذا المقال بالاعتماد على:
- مراجع أكاديمية من جامعات ومؤسسات علمية عالمية مرموقة
- دراسات وأوراق بحثية منشورة في مجلات علمية محكّمة
- كتب مرجعية معتمدة في تدريس التفاضل والتكامل عالمياً
نحن نُقدّر ملاحظاتكم ونرحب بأي تصحيحات أو اقتراحات لتحسين المحتوى. المصادر المُستخدمة مذكورة بشكل كامل في نهاية المقال للتحقق والتوسع.
المعلومات الواردة في هذا المقال مُقدَّمة لأغراض تعليمية وتثقيفية فقط، ولا تُغني عن الرجوع إلى الكتب الأكاديمية المعتمدة والمناهج الدراسية الرسمية. يُنصح الطلاب والباحثون بالتحقق من المعلومات الرياضية من مصادر أكاديمية موثوقة قبل استخدامها في الاختبارات أو الأبحاث العلمية.
موسوعة خلية العلمية (khalieah.com) تسعى لتقديم محتوى دقيق ومُحدَّث، لكنها لا تتحمل مسؤولية أي أخطاء قد تظهر أو أي استخدام غير صحيح للمعلومات المذكورة.
تمت مراجعة هذا المقال من قبل هيئة التحرير العلمية في موسوعة خلية العلمية
آخر تحديث: يناير 2026
لأي استفسارات أو ملاحظات، يُرجى التواصل معنا
هل أنت مستعد لتحويل المعرفة النظرية إلى مهارة عملية؟





