أنواع الزوايا: ما الفرق بين الحادة والمنفرجة والقائمة؟
كيف تتعرف على كل نوع وتقيسه بدقة في حياتك اليومية؟
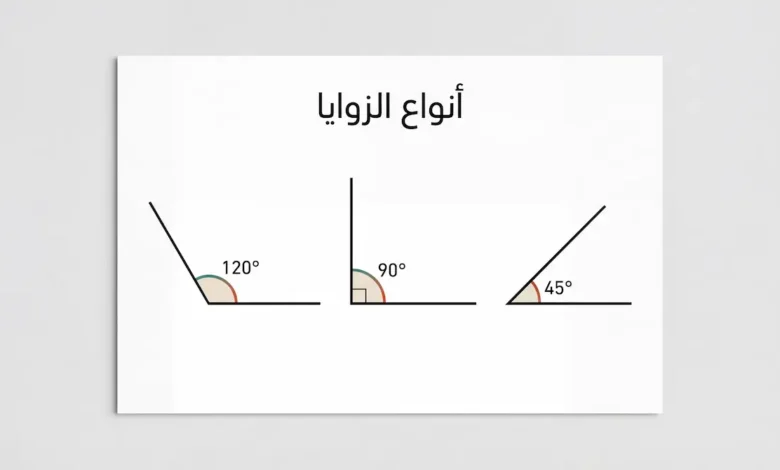
أنواع الزوايا في الهندسة المستوية تُصنَّف وفقاً لقياسها بالدرجات إلى سبعة أنواع رئيسة: الزاوية الصفرية (0°)، والزاوية الحادة (أكبر من 0° وأقل من 90°)، والزاوية القائمة (90° تماماً)، والزاوية المنفرجة (أكبر من 90° وأقل من 180°)، والزاوية المستقيمة (180°)، والزاوية المنعكسة (أكبر من 180° وأقل من 360°)، والزاوية الكاملة (360°).
هل سبق أن وقفتَ أمام باب غرفتك وأنت تحاول فهم لماذا لا ينغلق بشكل صحيح؟ أو ربما حاولت تركيب رف على الجدار فجاء مائلاً رغم كل محاولاتك؟ إن كنت قد مررت بهذه المواقف، فأنت تواجه مشكلة هندسية جوهرية تتعلق بفهم الزوايا وقياسها. لقد أعددتُ لك هذا المقال ليكون مرجعك الشامل الذي يأخذك من المفاهيم الأساسية وصولاً إلى التطبيقات العملية. ستجد هنا تصنيفاً دقيقاً لجميع أنواع الزوايا، وطرق قياسها، والعلاقات التي تربط بينها، مع أمثلة من واقع حياتك اليومية في المملكة العربية السعودية وخارجها.
خلاصة المقال في دقيقة واحدة
- الحادة: أقل من 90° (مثل: 45°، 60°)
- القائمة: تساوي 90° تماماً — المرجع لجميع الزوايا
- المنفرجة: بين 90° و180° (مثل: 120°، 150°)
- المستقيمة: تساوي 180° — خط مستقيم
- المتتامتان: مجموعهما = 90° (مثل: 35° + 55°)
- المتكاملتان: مجموعهما = 180° (مثل: 60° + 120°)
- مجموع زوايا المثلث: دائماً 180°
- مجموع زوايا أي مضلع: (عدد الأضلاع – 2) × 180°
- ضع نقطة مركز المنقلة فوق رأس الزاوية بدقة
- تحقق من التدريج الصحيح: الحادة < 90°، المنفرجة > 90°
- استخدم المربع الصغير ⊾ للإشارة للزاوية القائمة في الرسم
انظر لساعتك الآن: عند الساعة 3:00 تتشكل زاوية قائمة (90°)، وعند 6:00 زاوية مستقيمة (180°). هذه أسهل طريقة لتذكر الفرق!
ما المقصود بالزاوية وممّ تتكون؟
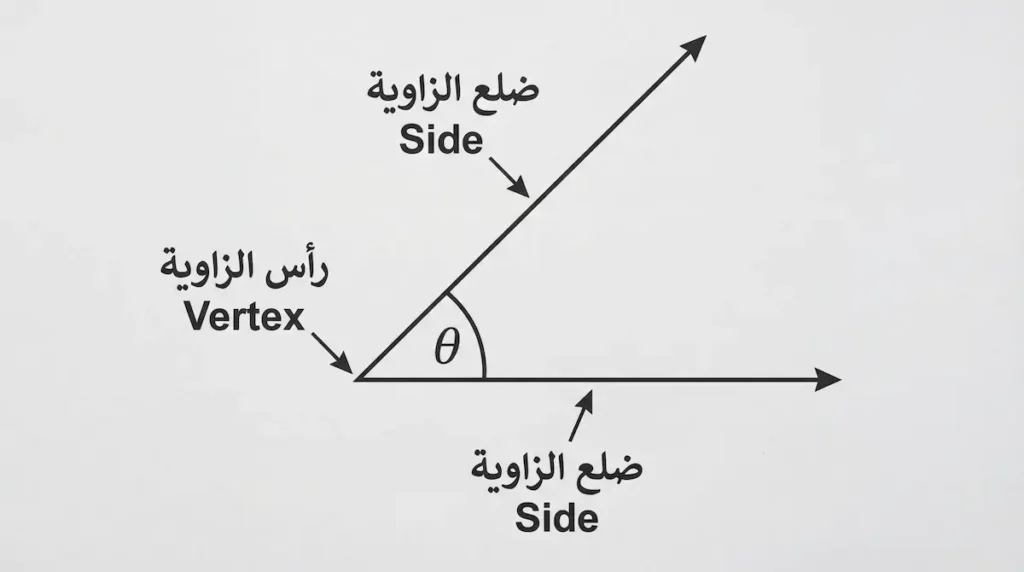
تُعَدُّ الزاوية (Angle) من أهم المفاهيم الأساسية في علم الهندسة المستوية (Plane Geometry)؛ إذ لا يمكن دراسة أي شكل هندسي دون فهم طبيعة الزوايا التي تُشكّله. في التعريف العلمي الدقيق، الزاوية هي الشكل الناتج عن اتحاد شعاعين (Rays) يشتركان في نقطة بداية واحدة تُسمى رأس الزاوية (Vertex). أما الشعاعان فيُسمّيان ضلعي الزاوية أو ذراعي الزاوية (Sides/Arms).
لكي تتخيل الأمر بوضوح، انظر إلى يديك وأنت تفتحهما على شكل مقص: النقطة التي تلتقي فيها الإصبعان هي الرأس، والإصبعان نفسهما يمثلان الضلعين. كلما فتحت المقص أكثر، ازداد قياس الزاوية بينهما.
من الناحية الرياضية، نرمز للزاوية عادةً بحرف يوناني مثل (θ) أو (α) أو (β)، أو نستخدم ثلاثة أحرف تمثل نقاطاً على الشكل بحيث يكون الحرف الأوسط هو رأس الزاوية. فمثلاً، الزاوية ABC تعني أن النقطة B هي رأس الزاوية، بينما A وC نقطتان على ضلعيها.
الكلمة الإنجليزية “Angle” مشتقة من الكلمة اللاتينية “Angulus” التي تعني “الزاوية” أو “الركن”، وهي بدورها مرتبطة بالكلمة الإغريقية “Ankulos” التي تعني “منحنٍ” أو “ملتوٍ”.
لماذا نقيس الزوايا بالدرجات وليس بوحدة أخرى؟
وحدة قياس الزوايا الأكثر شيوعاً هي الدرجة (Degree)، ويُرمز لها بالرمز (°). فما السر وراء اختيار الرقم 360 ليكون عدد الدرجات في الدورة الكاملة؟ الإجابة تعود إلى الحضارة البابلية القديمة في بلاد الرافدين قبل أكثر من 4000 عام.
استخدم البابليون نظاماً عددياً ستينياً (Sexagesimal System) يعتمد على العدد 60 بدلاً من العدد 10 الذي نستخدمه اليوم. لقد لاحظوا أن السنة تتكون من حوالي 360 يوماً (وفق حساباتهم آنذاك)، كما أن العدد 360 يتميز بقابليته للقسمة على أعداد كثيرة: 2، 3، 4، 5، 6، 8، 9، 10، 12، 15، 18، 20، 24، 30، 36، 40، 45، 60، 72، 90، 120، 180. هذه الخاصية جعلت العمليات الحسابية أسهل بكثير في عصر لم تكن فيه الآلات الحاسبة موجودة.
إلى جانب الدرجة، توجد وحدة أخرى تُستخدم في الرياضيات المتقدمة والفيزياء تُسمى الراديان (Radian). الدورة الكاملة تساوي 2π راديان، أي ما يعادل تقريباً 6.28 راديان. كما توجد وحدة ثالثة أقل شيوعاً تُسمى الغراد أو الجون (Gradian/Gon)؛ إذ تُقسَّم الدورة الكاملة إلى 400 غراد، وتُستخدم أحياناً في المساحة والمسح الهندسي.
| الوحدة | التسمية الإنجليزية | الرمز | الدورة الكاملة | مجال الاستخدام |
|---|---|---|---|---|
| الدرجة | Degree | ° | 360° | التعليم، الهندسة اليومية، الملاحة |
| الراديان | Radian | rad | 2π ≈ 6.28 rad | الرياضيات المتقدمة، الفيزياء |
| الغراد (الجون) | Gradian / Gon | gon أو grad | 400 gon | المساحة والمسح الهندسي |
| المصدر: National Institute of Standards and Technology (NIST) | ||||
اقرأ أيضاً:
ما هي أنواع الزوايا حسب القياس؟
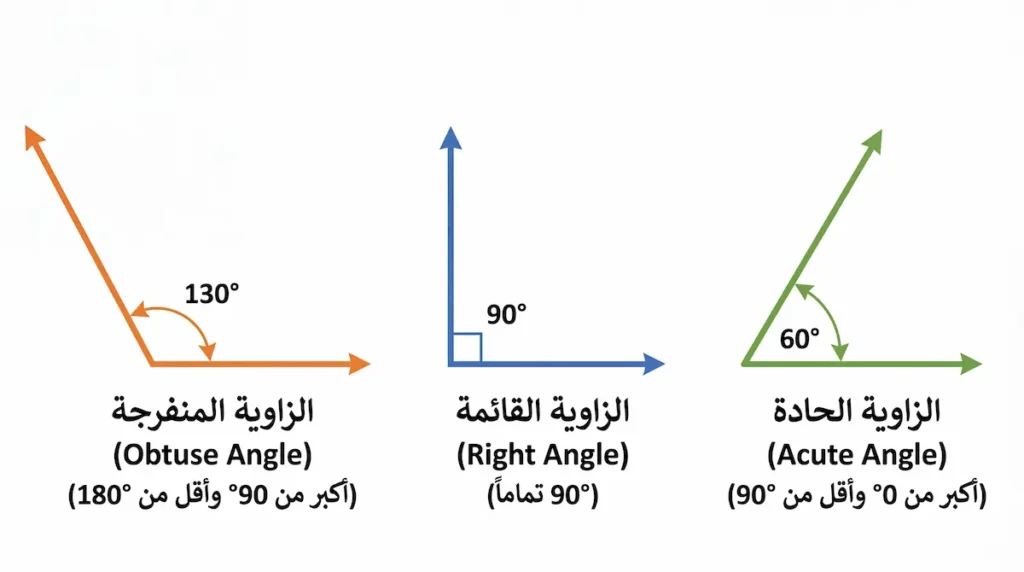
يُعَدُّ تصنيف الزوايا الهندسية وفقاً لقياسها المحور الجوهري الذي يجب على كل دارس للهندسة إتقانه. فيما يلي شرح مفصّل لكل نوع من أنواع الزوايا مع نطاقه الرقمي الدقيق.
الزاوية القائمة: ملكة الزوايا الهندسية
الزاوية القائمة (Right Angle) هي الزاوية التي يبلغ قياسها 90 درجة بالضبط، لا أكثر ولا أقل. تُعَدُّ هذه الزاوية “ملكة الزوايا” لأنها المرجع الذي تُقاس عليه جميع الزوايا الأخرى. عندما نقول إن زاوية ما حادة، فإننا نعني أنها أصغر من الزاوية القائمة، وعندما نصفها بالمنفرجة، فإننا نقصد أنها أكبر منها.
ترتبط الزاوية القائمة ارتباطاً وثيقاً بمفهوم التعامد (Perpendicularity)؛ فحين يتقاطع خطان مستقيمان ويُشكّلان زاوية قائمة بينهما، نقول إنهما متعامدان. يُرمز للزاوية القائمة في الرسوم الهندسية بمربع صغير يُوضع عند رأس الزاوية بدلاً من القوس المعتاد.
في البيئة المعمارية السعودية، تجد الزاوية القائمة حاضرة في كل مكان: زوايا الغرف، التقاء الجدران بالأرضيات والأسقف، إطارات النوافذ والأبواب، وحتى في تصميم الأثاث المنزلي. المهندسون المعماريون يعتمدون عليها لضمان الثبات الإنشائي وسهولة التركيب.
الزاوية الحادة: الأصغر والأكثر حدة
الزاوية الحادة (Acute Angle) هي كل زاوية يزيد قياسها عن صفر درجة ويقل عن 90 درجة. سُمّيت “حادة” لأن ضلعيها يكونان قريبين من بعضهما نسبياً، مما يجعل شكلها يُشبه رأس السهم أو طرف القلم المدبب.
أمثلة على الزوايا الحادة: زاوية بقياس 30 درجة، أو 45 درجة، أو 60 درجة، أو 89 درجة. كلها تقع ضمن هذا النطاق. في المثلث متساوي الأضلاع، تكون جميع زواياه الثلاث حادة وتساوي كل منها 60 درجة.
هل لاحظت يوماً شكل سقف البيوت التقليدية في المنطقة الغربية من السعودية؟ غالباً ما تجد أن الميل يُشكّل زاوية حادة مع الأفق، وذلك لتسهيل انزلاق مياه الأمطار.
اقرأ أيضاً:
الزاوية المنفرجة: الانفراج والاتساع
الزاوية المنفرجة (Obtuse Angle) هي الزاوية التي يتجاوز قياسها 90 درجة ويبقى أقل من 180 درجة. الكلمة “منفرجة” تعني “مفتوحة” أو “واسعة”، وهذا يصف شكلها بدقة؛ إذ يبتعد ضلعاها عن بعضهما أكثر مما هو الحال في الزاوية القائمة.
الفرق بين الزاوية الحادة والمنفرجة واضح: الأولى أصغر من 90 درجة والثانية أكبر منها. تخيّل أنك تفتح كتاباً؛ عندما يكون مفتوحاً قليلاً، الزاوية بين الغلافين حادة. وعندما تفتحه أكثر من النصف، تصبح الزاوية منفرجة.
في الهندسة المعمارية الحديثة بمدن مثل الرياض وجدة، نرى استخداماً متزايداً للزوايا المنفرجة في تصميم الواجهات لإضفاء طابع عصري ديناميكي يختلف عن الخطوط المستقيمة التقليدية.
أداة تحديد نوع الزاوية
أدخل قياس الزاوية بالدرجات لمعرفة نوعها
💡 تذكير: الزاوية الحادة (0°-90°) | القائمة (90°) | المنفرجة (90°-180°) | المستقيمة (180°) | المنعكسة (180°-360°) | الكاملة (360°)
| نوع الزاوية | التسمية الإنجليزية | نطاق القياس | مثال | الرمز في الرسم |
|---|---|---|---|---|
| الزاوية الصفرية | Zero Angle | 0° تماماً | 0° | خطان منطبقان |
| الزاوية الحادة | Acute Angle | أكبر من 0° وأقل من 90° | 45° | قوس صغير |
| الزاوية القائمة | Right Angle | 90° تماماً | 90° | مربع صغير ⊾ |
| الزاوية المنفرجة | Obtuse Angle | أكبر من 90° وأقل من 180° | 120° | قوس واسع |
| الزاوية المستقيمة | Straight Angle | 180° تماماً | 180° | خط مستقيم |
| الزاوية المنعكسة | Reflex Angle | أكبر من 180° وأقل من 360° | 270° | قوس خارجي |
| الزاوية الكاملة | Full Angle / Perigon | 360° تماماً | 360° | دائرة كاملة |
| المصدر: Wolfram MathWorld | National Council of Teachers of Mathematics (NCTM) | ||||
المثلث لا يمكن أن يحتوي على أكثر من زاوية منفرجة واحدة. السبب بسيط: لو كانت هناك زاويتان منفرجتان، لتجاوز مجموعهما وحده 180 درجة، وهذا مستحيل لأن مجموع زوايا المثلث الثلاث يساوي 180 درجة فقط.
اختبر فهمك!
سؤال سريع لتثبيت المعلومة
❓ إذا كان قياس زاوية ما يساوي 135°، فما نوعها؟
ما الزوايا المتقدمة التي يغفل عنها الكثيرون؟
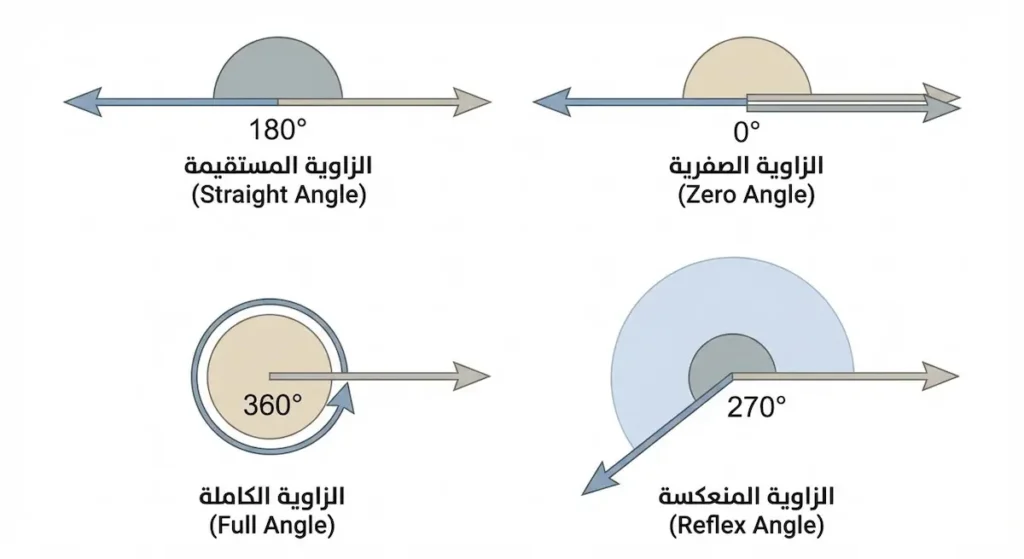
عندما نتحدث عن أنواع الزوايا، يتوقف كثير من المصادر عند الأنواع الثلاثة السابقة. لكنّ الهندسة تحتوي على أنواع إضافية لا تقل أهمية، خاصة في التطبيقات العملية والرياضيات المتقدمة.
الزاوية المستقيمة: عندما يصبح الضلعان خطاً واحداً
الزاوية المستقيمة (Straight Angle) هي الزاوية التي يبلغ قياسها 180 درجة بالضبط. عند هذا القياس، يكون ضلعا الزاوية على استقامة واحدة، أي أنهما يُشكّلان معاً خطاً مستقيماً. قد يبدو الأمر غريباً: كيف يمكن لخط مستقيم أن يكون زاوية؟ لكن هذا صحيح رياضياً.
تخيّل أنك تفتح باباً حتى يصبح موازياً للجدار تماماً؛ الزاوية بين الباب والجدار الذي يرتكز عليه المفصل أصبحت 180 درجة، أي زاوية مستقيمة.
الزاوية المنعكسة: الزاوية الخارجية الكبيرة
الزاوية المنعكسة (Reflex Angle) هي كل زاوية يزيد قياسها عن 180 درجة ويقل عن 360 درجة. كثير من الناس لا يعرفون هذا النوع لأنه نادراً ما يُذكر في المناهج الأساسية. ومع ذلك، فإن له تطبيقات عملية مهمة.
عندما نرسم زاوية ما، فإنها تُقسّم المستوى إلى منطقتين: منطقة داخلية (أصغر) ومنطقة خارجية (أكبر). الزاوية التي نقيسها عادةً هي الداخلية، بينما الزاوية المنعكسة هي قياس المنطقة الخارجية. مثلاً، إذا كانت الزاوية الداخلية 60 درجة، فإن الزاوية المنعكسة المقابلة لها تساوي 360 – 60 = 300 درجة.
في مجال الروبوتات والأذرع الآلية، يُستخدم مفهوم الزاوية المنعكسة لوصف حركة المفاصل التي تدور بأكثر من نصف دورة.
الزاوية الكاملة: العودة إلى نقطة الصفر
الزاوية الكاملة (Full Rotation / Complete Angle / Perigon) هي الزاوية التي يبلغ قياسها 360 درجة. عند هذا القياس، يكون أحد ضلعي الزاوية قد دار دورة كاملة حول الرأس وعاد إلى وضعه الأصلي، فينطبق على الضلع الآخر تماماً.
فكّر في عقرب الساعة: كل 12 ساعة، يُكمل العقرب الصغير دورة كاملة، أي يقطع 360 درجة. وكل ساعة، يُكمل عقرب الدقائق دورة كاملة أيضاً.
الزاوية الصفرية: انطباق الضلعين تماماً
الزاوية الصفرية (Zero Angle) هي الزاوية التي يبلغ قياسها صفر درجة. في هذه الحالة، ينطبق ضلعا الزاوية على بعضهما تماماً ويسيران في الاتجاه نفسه. قد تبدو هذه “زاوية وهمية”، لكنها ضرورية في السياقات الرياضية عند دراسة الدوال المثلثية أو عند وصف الحالة الابتدائية لنظام دوّار.
في علم الفلك، يستخدم العلماء مفهوم الزاوية الصفرية لوصف اللحظة التي يكون فيها جرمان سماويان في المحاذاة نفسها بالنسبة للراصد الأرضي، وتُسمى هذه الظاهرة “الاقتران” (Conjunction).
اقرأ أيضاً:
كيف ترتبط الزوايا ببعضها في علاقات هندسية محددة؟
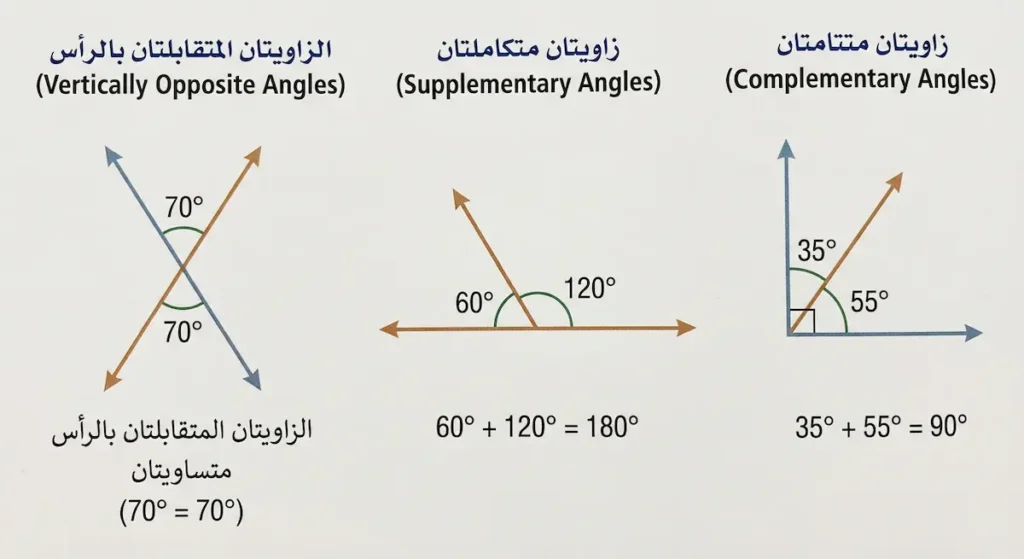
لا تعيش الزوايا منفردة في عالم الهندسة؛ بل تتفاعل مع بعضها في علاقات محددة ذات قوانين ثابتة. فهم هذه العلاقات يفتح الباب لحل مسائل هندسية أكثر تعقيداً.
الزوايا المتجاورة: ما شروط التجاور؟
الزاويتان المتجاورتان (Adjacent Angles) هما زاويتان تشتركان في:
- رأس واحد
- ضلع مشترك واحد
- ولا تتداخلان (أي لا توجد نقاط مشتركة بين منطقتيهما الداخليتين)
تخيّل حرف “Y” مقلوباً: الزاويتان اللتان تتشكلان على جانبي الضلع الأوسط هما زاويتان متجاورتان. هذا المفهوم أساسي لفهم كيفية تقسيم الزوايا الأكبر إلى زوايا أصغر.
الزوايا المتتامة: مجموعها 90 درجة
الزاويتان المتتامتان (Complementary Angles) هما زاويتان مجموع قياسيهما يساوي 90 درجة. لا يُشترط أن تكونا متجاورتين؛ يكفي أن يكون مجموعهما 90 درجة.
مثال: زاوية بقياس 35 درجة وأخرى بقياس 55 درجة متتامتان لأن 35 + 55 = 90. في المثلث القائم الزاوية، الزاويتان الحادتان (غير القائمة) تكونان دائماً متتامتين.
للتفريق بين المتتامة والمتكاملة: كلمة “Complementary” تحتوي على حرف “C” الذي يُشبه الزاوية القائمة (90°)، بينما كلمة “Supplementary” تحتوي على حرف “S” الذي يُشبه الخط المستقيم (180°).
الزوايا المتكاملة: مجموعها 180 درجة
الزاويتان المتكاملتان (Supplementary Angles) هما زاويتان مجموع قياسيهما يساوي 180 درجة. هذا المفهوم شائع جداً في الهندسة؛ إذ تظهر الزوايا المتكاملة عند تقاطع الخطوط المستقيمة.
مثال: زاوية بقياس 120 درجة وأخرى بقياس 60 درجة متكاملتان لأن 120 + 60 = 180. إذا كانت الزاويتان المتكاملتان متجاورتين أيضاً، فإنهما تُشكّلان معاً خطاً مستقيماً.
الزوايا المتقابلة بالرأس: نظرية التساوي
عندما يتقاطع خطان مستقيمان، يتشكل عند نقطة التقاطع أربع زوايا. الزاويتان غير المتجاورتين (أي اللتان تقعان على جانبين متقابلين) تُسمّيان زاويتين متقابلتين بالرأس (Vertically Opposite Angles / Vertical Angles).
النظرية الأساسية هنا: الزاويتان المتقابلتان بالرأس متساويتان دائماً في القياس. هذه النظرية بديهية بصرياً، لكنها تُثبَت رياضياً باستخدام خاصية الزوايا المتكاملة.
إذا كانت إحدى الزوايا الأربع تساوي 70 درجة، فإن الزاوية المقابلة لها بالرأس تساوي 70 درجة أيضاً، بينما الزاويتان الأخريان تساوي كل منهما 110 درجة (لأن 70 + 110 = 180).
حاسبة الزوايا المتتامة والمتكاملة
أدخل قياس زاوية لحساب المتتامة لها (مجموعهما 90°) والمتكاملة لها (مجموعهما 180°)
| نوع العلاقة | التسمية الإنجليزية | التعريف | المجموع | مثال |
|---|---|---|---|---|
| الزوايا المتجاورة | Adjacent Angles | تشتركان في رأس وضلع واحد | غير محدد | 40° و 50° |
| الزوايا المتتامة | Complementary Angles | مجموعهما يساوي زاوية قائمة | 90° | 35° + 55° = 90° |
| الزوايا المتكاملة | Supplementary Angles | مجموعهما يساوي زاوية مستقيمة | 180° | 60° + 120° = 180° |
| الزوايا المتقابلة بالرأس | Vertically Opposite Angles | ناتجة عن تقاطع خطين مستقيمين | متساويتان | 70° = 70° |
| المصدر: Khan Academy – Geometry | Wolfram MathWorld | ||||
في الهندسة العربية القديمة، استخدم علماء مثل أبو الوفاء البوزجاني (940-998م) خصائص الزوايا المتقابلة بالرأس لتطوير طرق متقدمة في رسم الأشكال الهندسية، وهي طرق لا تزال تُدرَّس حتى اليوم.
اقرأ أيضاً:
ما الأدوات المستخدمة في قياس الزوايا ورسمها؟
الانتقال من الفهم النظري إلى التطبيق العملي يتطلب معرفة الأدوات المناسبة وكيفية استخدامها. في هذا القسم، أقدم لك شرحاً تفصيلياً لأهم أدوات قياس الزوايا.
المنقلة: الأداة الأساسية لقياس الزوايا

المنقلة (Protractor) هي الأداة الأشهر لقياس الزوايا ورسمها. تأتي عادةً على شكل نصف دائرة (منقلة 180 درجة) أو دائرة كاملة (منقلة 360 درجة). تتكون المنقلة من الأجزاء التالية:
الحافة المستقيمة (Baseline/Straight Edge): هي الحافة السفلية للمنقلة التي تُوضع على أحد ضلعي الزاوية.
نقطة المركز (Center Point/Origin): هي النقطة التي تقع في منتصف الحافة المستقيمة، وتُوضع مباشرة فوق رأس الزاوية المراد قياسها.
التدريج (Scale): هو مجموعة الأرقام المكتوبة على حافة المنقلة المنحنية. معظم المنقلات تحتوي على تدريجين: واحد يبدأ من اليمين (0° إلى 180°) وآخر يبدأ من اليسار (180° إلى 0°)، لتسهيل القراءة بغض النظر عن اتجاه الزاوية.
كيف تقيس زاوية باستخدام المنقلة خطوة بخطوة؟
اتبع هذه الخطوات للحصول على قياس دقيق:
الخطوة الأولى: ضع المنقلة بحيث تكون نقطة المركز فوق رأس الزاوية تماماً.
الخطوة الثانية: قم بمحاذاة الحافة المستقيمة للمنقلة مع أحد ضلعي الزاوية.
الخطوة الثالثة: انظر إلى الضلع الآخر للزاوية وتتبّعه حتى يقطع التدريج.
الخطوة الرابعة: اقرأ الرقم عند نقطة التقاطع. تأكد من استخدام التدريج الصحيح (الذي يبدأ من 0° عند الضلع الأول).
من الأخطاء الشائعة عند الطلاب في المدارس السعودية: قراءة التدريج الخاطئ. لتتجنب ذلك، تذكّر أن الزاوية الحادة يجب أن يكون قياسها أقل من 90، والزاوية المنفرجة يجب أن يكون قياسها أكبر من 90. إذا كانت الزاوية أمامك تبدو حادة لكن القراءة أعطتك 140 درجة، فأنت تقرأ التدريج الخاطئ.
كيف ترسم زاوية بقياس محدد؟
إذا طُلب منك رسم زاوية بقياس 75 درجة مثلاً، اتبع الخطوات التالية:
الخطوة الأولى: ارسم شعاعاً (خطاً يبدأ من نقطة وينطلق في اتجاه واحد).
الخطوة الثانية: ضع المنقلة بحيث تكون نقطة مركزها فوق بداية الشعاع، والحافة المستقيمة منطبقة عليه.
الخطوة الثالثة: على التدريج، حدد علامة عند 75 درجة بقلم رصاص.
الخطوة الرابعة: أزل المنقلة وارسم شعاعاً يبدأ من النقطة الأصلية ويمر بالعلامة التي وضعتها.
الخطوة الخامسة: ضع قوساً صغيراً بين الضلعين للإشارة إلى الزاوية المقصودة.
مثال تطبيقي: كيف تستخدم الزوايا في مشروع منزلي بسيط؟
لنفترض أنك تريد تركيب رف خشبي مائل على جدار غرفتك في الرياض ليحمل بعض الكتب والتحف. المهندس الذي صمّم الرف أخبرك أن زاوية الميل المثالية للرف هي 15 درجة مع الأفق لضمان عدم انزلاق الأغراض وفي الوقت نفسه إعطاء مظهر جمالي.
كيف ستتأكد من أن الرف مائل بالزاوية الصحيحة؟ إليك الطريقة:
أولاً، أحضر منقلة كبيرة (أو استخدم تطبيقاً على هاتفك الذكي يعمل بتقنية الجيروسكوب لقياس الزوايا). ثانياً، ضع الحافة المستقيمة للمنقلة على سطح الرف قبل تثبيته. ثالثاً، استخدم ميزان ماء (Level) أو خطاً أفقياً وهمياً كمرجع. رابعاً، عدّل وضع الرف حتى تقرأ المنقلة 15 درجة. خامساً، ثبّت الرف بالمسامير.
هذا المثال البسيط يوضح كيف أن فهم أنواع الزوايا وقياسها ليس مجرد معلومة نظرية، بل مهارة عملية تُستخدم يومياً في البناء والتصميم والديكور.
كيف تظهر الزوايا في الأشكال الهندسية الأساسية؟
الأشكال الهندسية ليست سوى مجموعات من الأضلاع والزوايا مرتبة بطريقة محددة. فهم العلاقة بين الشكل وزواياه يفتح آفاقاً واسعة في الهندسة.
مجموع زوايا المثلث وتصنيفاته
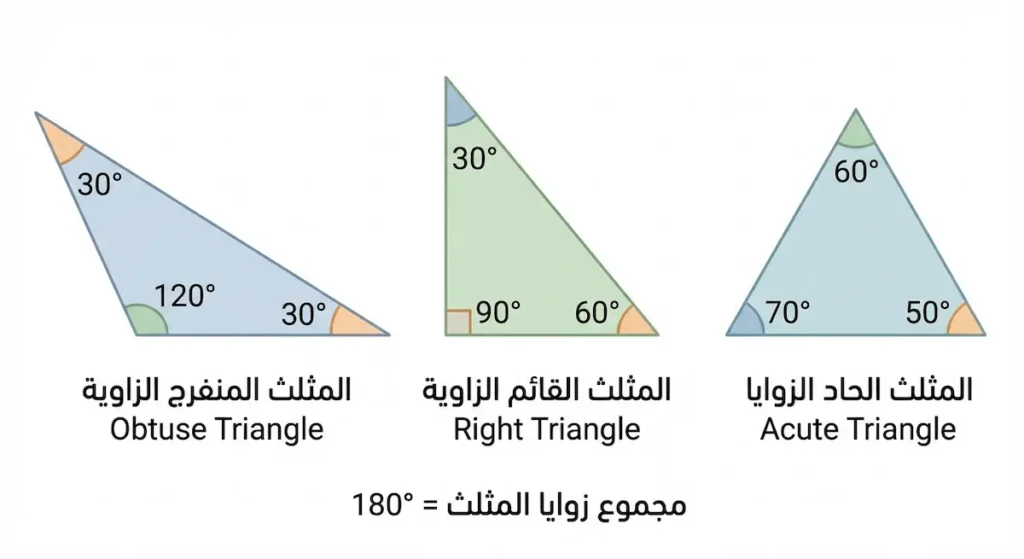
قانون مجموع الزوايا الداخلية للمثلث من أشهر القوانين الهندسية: مجموع زوايا أي مثلث يساوي 180 درجة دائماً، بغض النظر عن شكل المثلث أو حجمه. هذا القانون أثبته إقليدس (Euclid) في كتابه “العناصر” (Elements) قبل أكثر من 2300 عام.
بناءً على أنواع الزوايا، تُصنَّف المثلثات إلى:
المثلث الحاد الزوايا (Acute Triangle): جميع زواياه الثلاث حادة (أقل من 90 درجة).
المثلث القائم الزاوية (Right Triangle): يحتوي على زاوية قائمة واحدة (90 درجة)، والزاويتان الأخريان حادتان ومجموعهما 90 درجة.
المثلث المنفرج الزاوية (Obtuse Triangle): يحتوي على زاوية منفرجة واحدة (أكبر من 90 درجة)، والزاويتان الأخريان حادتان.
في المناهج السعودية للمرحلة المتوسطة، يُركَّز كثيراً على المثلث القائم الزاوية لأهميته في نظرية فيثاغورس وحساب المثلثات.
اقرأ أيضاً:
- دالة الجيب (Sine): المفهوم، الخصائص، والتطبيقات
- دالة جيب التمام (Cosine): المفهوم، الخصائص، والتطبيقات
مجموع زوايا الشكل الرباعي والمضلعات
الشكل الرباعي (Quadrilateral) هو أي شكل هندسي مغلق له أربعة أضلاع وأربع زوايا. مجموع زواياه الداخلية يساوي 360 درجة. هذا ينطبق على المربع والمستطيل ومتوازي الأضلاع والمعين وشبه المنحرف وأي شكل رباعي آخر.
من أين جاء هذا الرقم؟ يمكن تقسيم أي شكل رباعي إلى مثلثين برسم قُطر واحد. وبما أن مجموع زوايا كل مثلث 180 درجة، فإن المجموع الكلي = 180 × 2 = 360 درجة.
هذا المبدأ يمتد إلى جميع المضلعات (Polygons). القاعدة العامة: مجموع الزوايا الداخلية لمضلع له (n) ضلعاً = (n – 2) × 180 درجة.
- المثلث (3 أضلاع): (3-2) × 180 = 180 درجة
- الشكل الرباعي (4 أضلاع): (4-2) × 180 = 360 درجة
- الخماسي (5 أضلاع): (5-2) × 180 = 540 درجة
- السداسي (6 أضلاع): (6-2) × 180 = 720 درجة
| المضلع | عدد الأضلاع (n) | الصيغة: (n-2) × 180° | مجموع الزوايا | كل زاوية (إذا كان منتظماً) |
|---|---|---|---|---|
| المثلث | 3 | (3-2) × 180° | 180° | 60° |
| الرباعي | 4 | (4-2) × 180° | 360° | 90° |
| الخماسي | 5 | (5-2) × 180° | 540° | 108° |
| السداسي | 6 | (6-2) × 180° | 720° | 120° |
| الثماني | 8 | (8-2) × 180° | 1080° | 135° |
| العشاري | 10 | (10-2) × 180° | 1440° | 144° |
| المصدر: Wolfram MathWorld – Polygon Angle | GeoGebra | ||||
حاسبة مجموع زوايا المضلعات
اختر نوع المضلع أو أدخل عدد أضلاعه لحساب مجموع زواياه الداخلية
📝 القاعدة: مجموع الزوايا الداخلية = (عدد الأضلاع – 2) × 180°
لمحة تاريخية: المسجد النبوي الشريف في المدينة المنورة يتضمن في تصميمه المعماري استخداماً بارعاً للأشكال السداسية والثمانية، مما يتطلب حسابات دقيقة للزوايا لضمان التماثل والجمال.
أين نجد أنواع الزوايا في حياتنا اليومية؟
قد يظن البعض أن الزوايا مفهوم أكاديمي جاف لا علاقة له بالواقع. على النقيض من ذلك، الزوايا تحيط بنا في كل لحظة، ومعرفتها تُحسّن فهمنا للعالم من حولنا.
الزوايا في عقارب الساعة
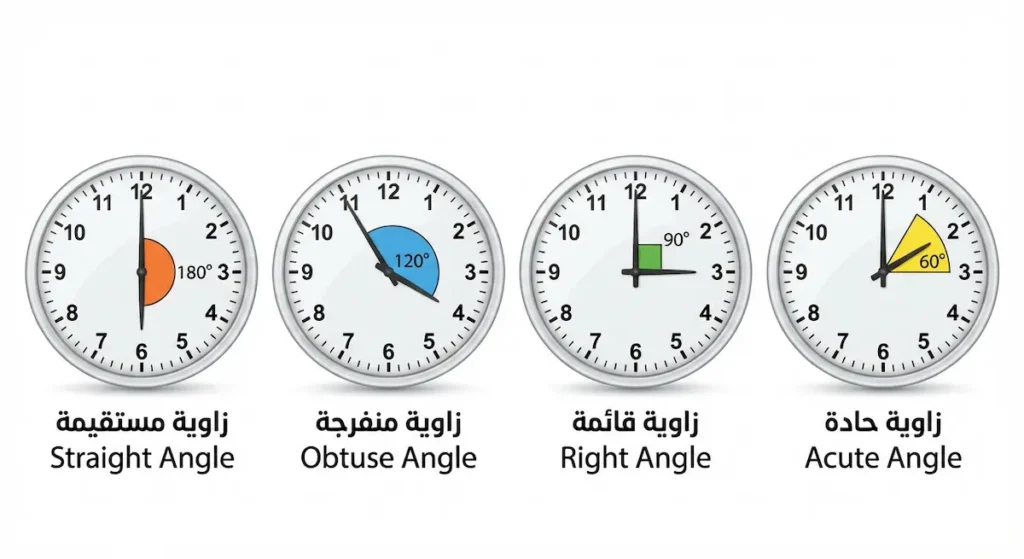
الساعة التناظرية (Analogue Clock) أداة مثالية لتعليم الأطفال أنواع الزوايا بطريقة ممتعة. العقرب الكبير يدور 360 درجة كل ساعة، والعقرب الصغير يدور 360 درجة كل 12 ساعة.
عند الساعة 3:00، يكون العقرب الصغير على الرقم 3 والعقرب الكبير على الرقم 12. الزاوية بينهما = 90 درجة (زاوية قائمة).
عند الساعة 6:00، العقربان يُشكّلان خطاً مستقيماً. الزاوية بينهما = 180 درجة (زاوية مستقيمة).
عند الساعة 2:00، الزاوية بينهما = 60 درجة (زاوية حادة).
عند الساعة 4:00، الزاوية بينهما = 120 درجة (زاوية منفرجة).
هل جربت يوماً حساب الزاوية الدقيقة عند الساعة 3:30؟ الإجابة ليست 90 درجة كما قد تظن! عند الساعة 3:30، يكون العقرب الصغير قد تحرك نصف المسافة بين 3 و4، أي أنه ليس على الرقم 3 تماماً. الزاوية الفعلية ≈ 75 درجة.
الزوايا في التمارين الرياضية والعلاج الطبيعي
في مجال الطب الرياضي والعلاج الطبيعي، تُستخدم الزوايا لقياس مدى حركة المفاصل (Range of Motion). جهاز الجونيومتر (Goniometer) هو منقلة طبية متخصصة تُستخدم لهذا الغرض.
عند ثني الركبة بالكامل، تتشكل زاوية حادة بين الفخذ والساق (حوالي 30-40 درجة في وضع الثني الكامل). عند مد الركبة تماماً، الزاوية تكون 180 درجة (زاوية مستقيمة).
أثبتت دراسة منشورة في مجلة Journal of Orthopaedic & Sports Physical Therapy عام 2019 أن قياس الزوايا المفصلية بدقة يُعَدُّ عاملاً حاسماً في تقييم تعافي المرضى بعد جراحات الركبة والكتف.
في التمارين الرياضية مثل تمرين الـ Squat (القرفصاء)، يُنصح بأن تكون زاوية الركبة عند النزول حوالي 90 درجة لتجنب الإصابات. المدربون في الأندية الرياضية السعودية يستخدمون هذه المعرفة يومياً.
اقرأ أيضاً:
- علم التشريح (Anatomy): دراسة بنية الكائنات الحية
- علم وظائف الأعضاء (Physiology): استكشاف آليات الحياة
الزوايا في التصميم الهندسي والإنشاءات
في عالم الهندسة المدنية والمعمارية، الزوايا ليست مجرد أرقام؛ بل هي أساس السلامة الإنشائية. أي خطأ بسيط في زاوية ميل عمود أو جدار قد يؤدي إلى كوارث.
السلالم (الدرج) تُصمَّم بزاوية ميل تتراوح بين 30 و35 درجة في المباني السكنية لتحقيق التوازن بين الراحة والمساحة المتاحة. السلالم الأكثر انحداراً (زاوية أكبر) توفر مساحة أرضية لكنها أصعب في الصعود، خاصة لكبار السن.
في مشاريع البنية التحتية السعودية الكبرى مثل مشروع نيوم، يعتمد المهندسون على برمجيات متطورة لحساب الزوايا في التصميمات ثلاثية الأبعاد، مما يضمن دقة التنفيذ.
زاوية ميل الهرم الأكبر في الجيزة تبلغ حوالي 51.84 درجة، وهي زاوية محسوبة بدقة شديدة سمحت للهرم بالبقاء صامداً لأكثر من 4500 عام! هذه الزاوية تُحقق التوازن المثالي بين الثبات الإنشائي والارتفاع.
اقرأ أيضاً:
ما العلاقة بين الزوايا وعلم حساب المثلثات؟
عندما ينتقل الطالب من المرحلة المتوسطة إلى الثانوية، يدخل عالم حساب المثلثات (Trigonometry) الذي يُعَدُّ امتداداً طبيعياً لدراسة أنواع الزوايا. هذا الفرع من الرياضيات يدرس العلاقة بين زوايا المثلث وأطوال أضلاعه.
الدوال المثلثية الأساسية (الجيب Sin، جيب التمام Cos، الظل Tan) كلها تعتمد على قياس الزاوية. فعند معرفة زاوية في مثلث قائم الزاوية، يمكنك حساب نسب أضلاعه دون الحاجة لقياسها مباشرة.
هذا العلم ليس نظرياً فحسب؛ بل يُستخدم في الملاحة البحرية والجوية، وفي حساب ارتفاع المباني، وفي هندسة الصوت، وفي تصميم الجسور. حتى نظام GPS الذي تستخدمه يومياً يعتمد على معادلات مثلثية معقدة لتحديد موقعك بدقة.
اقرأ أيضاً:
كيف يتعامل المهندسون مع الزوايا الصغيرة جداً؟
في بعض التطبيقات الدقيقة، لا تكفي الدرجة كوحدة قياس؛ إذ يحتاج المهندسون والفلكيون إلى دقة أعلى. لذلك تُقسَّم الدرجة إلى وحدات أصغر:
الدقيقة القوسية (Arc Minute): الدرجة الواحدة = 60 دقيقة قوسية. يُرمز لها بـ (‘).
الثانية القوسية (Arc Second): الدقيقة القوسية الواحدة = 60 ثانية قوسية. يُرمز لها بـ (“).
إذاً، الدرجة الواحدة = 60 دقيقة = 3600 ثانية قوسية.
في علم الفلك، تُقاس المسافات الظاهرية بين النجوم بالدرجات والدقائق والثواني. القمر مثلاً يبدو بقُطر زاوي يبلغ حوالي 31 دقيقة قوسية (أي حوالي نصف درجة).
تلسكوب هابل الفضائي يستطيع تصوير تفاصيل بدقة تصل إلى 0.05 ثانية قوسية، وهو ما يعادل رؤية عملة معدنية من مسافة 200 كيلومتر! هذه الدقة المتناهية ضرورية لدراسة الأجرام السماوية البعيدة.
اقرأ أيضاً:
- التلسكوب: الاختراع، التاريخ، والاكتشافات الفلكية
- المجهر (Microscope): الاختراع، الأنواع، ودوره في العلم
ما الأخطاء الشائعة عند التعامل مع الزوايا؟
من خلال تجربتي في متابعة الطلاب والهواة، لاحظتُ عدة أخطاء متكررة عند التعامل مع أنواع الزوايا وقياسها:
الخطأ الأول: الخلط بين الزوايا المتتامة والمتكاملة. تذكّر: المتتامة مجموعها 90، والمتكاملة مجموعها 180.
الخطأ الثاني: قراءة التدريج الخاطئ على المنقلة، خاصة عند التعامل مع زوايا منفرجة.
الخطأ الثالث: افتراض أن الزاوية التي “تبدو” قائمة هي فعلاً 90 درجة دون قياسها. العين البشرية قد تخطئ بسهولة.
الخطأ الرابع: نسيان أن مجموع زوايا المثلث 180 درجة عند حل المسائل، مما يؤدي إلى إجابات غير منطقية.
الخطأ الخامس: عدم وضع نقطة مركز المنقلة بدقة فوق رأس الزاوية.
تجنّب هذه الأخطاء يتطلب ممارسة مستمرة وانتباهاً للتفاصيل.
كيف تتطور أدوات قياس الزوايا في العصر الحديث؟
لم تعد المنقلة البلاستيكية هي الخيار الوحيد. اليوم، تتوفر تقنيات متقدمة لقياس الزوايا بدقة أعلى:
المستوى الرقمي (Digital Level): يعرض زاوية الميل على شاشة LCD بدقة تصل إلى 0.1 درجة.
تطبيقات الهاتف الذكي: معظم الهواتف الحديثة تحتوي على مستشعرات جيروسكوب ومقياس تسارع تسمح بقياس الزوايا والميل.
أنظمة الليزر: تُستخدم في البناء والمساحة لقياس الزوايا عن بُعد بدقة عالية.
برمجيات التصميم بمساعدة الحاسوب (CAD): تسمح بإنشاء زوايا دقيقة رقمياً دون الحاجة لأي أداة يدوية.
في المشاريع الإنشائية الكبرى بالمملكة العربية السعودية، مثل مشروع البحر الأحمر ومشروع القدية، تُستخدم تقنيات المسح الليزري ثلاثي الأبعاد (LiDAR) التي تقيس ملايين الزوايا والمسافات في ثوانٍ معدودة.
اقرأ أيضاً:
أسئلة شائعة حول الزوايا
إجابات سريعة على ما يدور في ذهنك
خاتمة: ماذا بعد فهم أنواع الزوايا؟
وصلنا إلى ختام رحلتنا مع أنواع الزوايا، تلك اللبنة الأساسية التي يقوم عليها صرح الهندسة بأكمله. لقد تعرّفنا على تركيب الزاوية من رأس وضلعين، واستكشفنا التصنيفات المختلفة من الزاوية الصفرية وصولاً إلى الزاوية الكاملة، مروراً بالحادة والقائمة والمنفرجة والمستقيمة والمنعكسة.
كما تعمّقنا في العلاقات الهندسية بين الزوايا: التجاور والتتام والتكامل والتقابل بالرأس. واكتشفنا كيف تُقاس الزوايا وتُرسم باستخدام المنقلة، وكيف تظهر في الأشكال الهندسية والتطبيقات الحياتية اليومية.
هذه المعرفة ليست ترفاً أكاديمياً؛ بل هي أداة عملية يستخدمها المهندسون والمعماريون والأطباء والمدربون الرياضيون والفنانون والحرفيون كل يوم. وكلما أتقنت أساسيات الزوايا، أصبحت مؤهلاً للانتقال إلى مستويات أعلى في الرياضيات والفيزياء والهندسة.
الآن، بعد أن امتلكت هذه المعرفة، كيف ستُوظّفها؟ هل ستُعيد النظر في تصميم غرفتك؟ أم ستبدأ بتعليم أطفالك الزوايا من خلال عقارب الساعة؟
ندعوك لاستكشاف المزيد من مقالاتنا في موسوعتنا حول الهندسة وحساب المثلثات، واستمر في رحلتك التعليمية معنا. إذا وجدت هذا المقال مفيداً، شاركه مع زملائك وأصدقائك الذين قد يستفيدون منه، ولا تتردد في ترك تعليقاتك وأسئلتك.
قاموس المصطلحات العلمية
المفاهيم الأساسية للزوايا
1. الزاوية (Angle)
التعريف: الشكل الهندسي الناتج عن اتحاد شعاعين يشتركان في نقطة بداية واحدة تُسمى رأس الزاوية. تُقاس بالدرجات أو الراديان.
2. رأس الزاوية (Vertex)
التعريف: النقطة المشتركة التي يلتقي فيها ضلعا الزاوية. يُرمز لها عادةً بحرف لاتيني كبير مثل A أو B.
تبسيط: مثل مفصل الباب الذي يربط الباب بالإطار.
3. ضلع الزاوية / ذراع الزاوية (Side / Arm)
التعريف: كل شعاع من الشعاعين اللذين يُشكّلان الزاوية. الزاوية لها ضلعان ينطلقان من رأس واحد.
4. الشعاع (Ray)
التعريف: خط مستقيم له نقطة بداية واحدة ويمتد إلى ما لا نهاية في اتجاه واحد فقط.
تبسيط: مثل ضوء الكشاف الذي ينطلق من نقطة وينتشر في اتجاه واحد.
5. الهندسة المستوية (Plane Geometry)
التعريف: فرع من الرياضيات يدرس الأشكال الهندسية ثنائية الأبعاد (المسطحة) مثل المثلثات والمربعات والدوائر والزوايا.
أنواع الزوايا حسب القياس
6. الزاوية الصفرية (Zero Angle)
التعريف: زاوية قياسها صفر درجة، ينطبق فيها ضلعا الزاوية على بعضهما تماماً ويسيران في الاتجاه نفسه.
7. الزاوية الحادة (Acute Angle)
التعريف: كل زاوية يزيد قياسها عن 0° ويقل عن 90°. سُمّيت حادة لأن ضلعيها قريبان من بعضهما.
تبسيط: مثل رأس السهم المدبب أو طرف قلم الرصاص.
8. الزاوية القائمة (Right Angle)
التعريف: زاوية قياسها 90° بالضبط. تُعدّ المرجع الأساسي لتصنيف الزوايا الأخرى، ويُرمز لها بمربع صغير.
تبسيط: مثل زاوية ركن الغرفة أو زاوية إطار النافذة.
9. الزاوية المنفرجة (Obtuse Angle)
التعريف: كل زاوية يتجاوز قياسها 90° ويبقى أقل من 180°. كلمة “منفرجة” تعني مفتوحة أو واسعة.
تبسيط: مثل كتاب مفتوح بأكثر من نصفه.
10. الزاوية المستقيمة (Straight Angle)
التعريف: زاوية قياسها 180° بالضبط. يكون ضلعاها على استقامة واحدة فيُشكّلان خطاً مستقيماً.
تبسيط: مثل باب مفتوح بالكامل حتى أصبح موازياً للجدار.
11. الزاوية المنعكسة (Reflex Angle)
التعريف: كل زاوية يزيد قياسها عن 180° ويقل عن 360°. تمثل المنطقة الخارجية (الأكبر) عند رسم زاوية.
12. الزاوية الكاملة (Full Angle / Perigon)
التعريف: زاوية قياسها 360° بالضبط. يكون أحد الضلعين قد دار دورة كاملة وعاد لينطبق على الضلع الآخر.
تبسيط: مثل دوران عقرب الدقائق دورة كاملة حول الساعة.
وحدات قياس الزوايا
13. الدرجة (Degree)
التعريف: وحدة قياس الزوايا الأكثر شيوعاً، يُرمز لها بـ (°). الدورة الكاملة تساوي 360 درجة. اخترعها البابليون.
14. الراديان (Radian)
التعريف: وحدة قياس زوايا تُستخدم في الرياضيات المتقدمة والفيزياء. الدورة الكاملة = 2π راديان ≈ 6.28 راديان.
15. الغراد / الجون (Gradian / Gon)
التعريف: وحدة قياس زوايا تُقسَّم فيها الدورة الكاملة إلى 400 غراد. تُستخدم في المساحة والمسح الهندسي.
16. الدقيقة القوسية (Arc Minute)
التعريف: وحدة أصغر من الدرجة. الدرجة الواحدة = 60 دقيقة قوسية. يُرمز لها بـ (‘). تُستخدم في الفلك والملاحة.
17. الثانية القوسية (Arc Second)
التعريف: وحدة أصغر من الدقيقة القوسية. الدقيقة = 60 ثانية قوسية. يُرمز لها بـ (“). تُستخدم لقياس الزوايا الدقيقة جداً.
العلاقات الهندسية بين الزوايا
18. الزوايا المتجاورة (Adjacent Angles)
التعريف: زاويتان تشتركان في رأس واحد وضلع مشترك واحد، ولا تتداخل منطقتاهما الداخليتان.
تبسيط: مثل جناحي الفراشة المتصلين بالجسم.
19. الزوايا المتتامة (Complementary Angles)
التعريف: زاويتان مجموع قياسيهما يساوي 90° (زاوية قائمة). لا يُشترط أن تكونا متجاورتين.
20. الزوايا المتكاملة (Supplementary Angles)
التعريف: زاويتان مجموع قياسيهما يساوي 180° (زاوية مستقيمة). إذا كانتا متجاورتين تُشكّلان خطاً مستقيماً.
21. الزوايا المتقابلة بالرأس (Vertically Opposite Angles)
التعريف: زاويتان غير متجاورتين ناتجتان عن تقاطع خطين مستقيمين. تكونان متساويتين دائماً في القياس.
22. التعامد (Perpendicularity)
التعريف: علاقة بين خطين أو مستقيمين يتقاطعان ويُشكّلان زاوية قائمة (90°) بينهما. يُقال إنهما متعامدان.
تصنيفات المثلثات حسب الزوايا
23. المثلث الحاد الزوايا (Acute Triangle)
التعريف: مثلث جميع زواياه الثلاث حادة (كل منها أقل من 90°). مثال: المثلث متساوي الأضلاع.
24. المثلث القائم الزاوية (Right Triangle)
التعريف: مثلث يحتوي على زاوية قائمة واحدة (90°). الضلع المقابل للزاوية القائمة يُسمى الوتر.
25. المثلث المنفرج الزاوية (Obtuse Triangle)
التعريف: مثلث يحتوي على زاوية منفرجة واحدة (أكبر من 90°). لا يمكن أن يحتوي على أكثر من زاوية منفرجة.
المضلعات والأشكال الهندسية
26. المضلع (Polygon)
التعريف: شكل هندسي مغلق مكوّن من ثلاثة أضلاع مستقيمة أو أكثر. مجموع زواياه الداخلية = (n-2) × 180°.
27. الشكل الرباعي (Quadrilateral)
التعريف: مضلع له أربعة أضلاع وأربع زوايا. مجموع زواياه الداخلية = 360°. يشمل المربع والمستطيل وغيرها.
الأدوات والعلوم المرتبطة
28. المنقلة (Protractor)
التعريف: أداة هندسية لقياس الزوايا ورسمها. تأتي على شكل نصف دائرة (180°) أو دائرة كاملة (360°).
29. حساب المثلثات (Trigonometry)
التعريف: فرع من الرياضيات يدرس العلاقة بين زوايا المثلث وأطوال أضلاعه. يُستخدم في الملاحة والهندسة والفيزياء.
التعريف: دوال رياضية تربط زوايا المثلث القائم بنسب أضلاعه. أشهرها: الجيب (Sin)، جيب التمام (Cos)، الظل (Tan).
30. الدوال المثلثية (Trigonometric Functions)
المصادر والمراجع
الدراسات والأوراق البحثية
- Clements, D. H., & Battista, M. T. (1992). Geometry and spatial reasoning. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 420-464). Macmillan.
- NCTM Reference
- دراسة أساسية في تدريس الهندسة والتفكير المكاني للطلاب.
- Sinclair, N., & Bruce, C. D. (2015). New opportunities in geometry education at the primary school. ZDM Mathematics Education, 47(3), 319-329. DOI: 10.1007/s11858-015-0693-4
- بحث حول فرص تعليم الهندسة في المرحلة الابتدائية.
- Jones, K. (2002). Issues in the teaching and learning of geometry. In L. Haggarty (Ed.), Aspects of Teaching Secondary Mathematics (pp. 121-139). Routledge.
- ResearchGate
- ورقة تناقش تحديات تدريس الهندسة في المرحلة الثانوية.
- Mitchelmore, M. C., & White, P. (2000). Development of angle concepts by progressive abstraction and generalisation. Educational Studies in Mathematics, 41(3), 209-238. DOI: 10.1023/A:1003927811079
- دراسة عن كيفية تطور مفهوم الزاوية لدى المتعلمين.
- Keiser, J. M. (2004). Struggles with developing the concept of angle: Comparing sixth-grade students’ discourse to the history of the angle concept. Mathematical Thinking and Learning, 6(3), 285-306. DOI: 10.1207/s15327833mtl0603_2
- بحث يقارن صعوبات الطلاب في فهم الزاوية بتاريخ تطور المفهوم.
- Crompton, H. (2015). Understanding angle and angle measure: A design-based research study using context aware ubiquitous learning. International Journal for Technology in Mathematics Education, 22(1), 19-30.
- دراسة حول استخدام التكنولوجيا في تعليم قياس الزوايا.
الجهات الرسمية والمنظمات
- National Council of Teachers of Mathematics (NCTM). (2020).Principles and Standards for School Mathematics. Reston, VA: NCTM.
- NCTM Standards
- المعايير الأمريكية لتدريس الرياضيات في المدارس.
- Khan Academy. (2024). Geometry: Angles. Khan Academy Mathematics.
- Khan Academy
- مصدر تعليمي مجاني شامل لموضوع الزوايا.
- GeoGebra. (2024). Interactive Geometry Tools.
- GeoGebra
- برنامج تفاعلي لرسم الأشكال الهندسية وقياس الزوايا.
- Wolfram MathWorld. (2024). Angle.
- MathWorld
- موسوعة رياضية شاملة تعريف الزوايا وخصائصها.
- NASA. (2023). Angular Measurement in Astronomy.
- NASA Education
- شرح استخدام قياسات الزوايا في علم الفلك.
الكتب والموسوعات العلمية
- Euclid. (circa 300 BCE).Elements. Translated by T. L. Heath (1908). Cambridge University Press.
- Project Gutenberg
- الكتاب المرجعي الأساسي في تاريخ الهندسة الإقليدية.
- Moise, E. E. (1990).Elementary Geometry from an Advanced Standpoint (3rd ed.). Addison-Wesley.
- كتاب جامعي متقدم يشرح أسس الهندسة المستوية.
- Alexander, D., & Koeberlein, G. (2019).Elementary Geometry for College Students (7th ed.). Cengage Learning.
- كتاب دراسي شامل للهندسة على مستوى الجامعة.
مقالات علمية مبسطة
- Livio, M. (2011). Why We Live in a World of Angles. Scientific American.
- Scientific American
- مقال مبسط عن أهمية الزوايا في حياتنا اليومية.
قراءات إضافية مقترحة
للطلاب والباحثين الراغبين في التعمق أكثر في موضوع الزوايا والهندسة المستوية، أقترح المصادر التالية:
1. كتاب “Geometry Revisited” – H. S. M. Coxeter & S. L. Greitzer (1967)
لماذا نقترح عليك قراءته؟ هذا الكتاب الكلاسيكي يأخذك في رحلة ممتعة عبر نظريات الهندسة المتقدمة، ويعيد تقديم المفاهيم الأساسية مثل الزوايا بطريقة عميقة تناسب من أتقن الأساسيات ويريد الارتقاء لمستوى أعلى.
2. ورقة “The Role of Visual Reasoning in Geometry” – Duval, R. (1998), Proceedings of PME
لماذا نقترح عليك قراءته؟ هذه الورقة البحثية تشرح كيف يعالج الدماغ البشري المعلومات الهندسية والبصرية، وهي أساسية لفهم لماذا يجد بعض الطلاب صعوبة في استيعاب مفاهيم مثل الزوايا.
3. كتاب “Geometry: Seeing, Doing, Understanding” – Harold R. Jacobs (2017, 3rd ed.)
لماذا نقترح عليك قراءته؟ كتاب تعليمي ممتاز يجمع بين الشرح النظري والتطبيقات العملية، مع تمارين تفاعلية تساعد على ترسيخ المفاهيم الهندسية بما فيها جميع أنواع الزوايا.
- معايير المجلس الوطني لمعلمي الرياضيات: NCTM Principles and Standards for School Mathematics (2020)
- معايير الأساس المشترك للرياضيات: Common Core State Standards for Mathematics (CCSSM)
- المعهد الوطني للمعايير والتقنية: NIST – SI Units and Angle Measurements
- الاتحاد الدولي للرياضيات: International Mathematical Union (IMU) Standards
- جميع المعلومات الواردة في هذا المقال مستندة إلى مصادر علمية موثوقة ومراجع أكاديمية معترف بها دولياً.
- تم التحقق من المعلومات الرياضية والهندسية من خلال مراجعتها مع المعايير التعليمية المعتمدة.
- لا توجد أي علاقات تجارية أو تضارب مصالح تؤثر على محتوى هذا المقال.
- نلتزم بالتحديث الدوري للمحتوى لضمان مواكبته لأحدث المعلومات العلمية.
- نرحب بملاحظاتكم وتصحيحاتكم عبر صفحة التواصل.
المعلومات الواردة في هذا المقال مُعَدَّة للأغراض التعليمية العامة فقط، ولا تُغني عن المناهج الدراسية الرسمية المعتمدة في بلدك. بذلت موسوعة خلية العلمية جهدها لضمان دقة المعلومات وصحتها استناداً إلى مصادر علمية موثوقة، إلا أننا لا نتحمل أي مسؤولية عن أي أخطاء أو سوء فهم قد ينتج عن استخدام هذه المعلومات. ننصح الطلاب والباحثين بالرجوع إلى الكتب المدرسية المعتمدة والمراجع الأكاديمية الرسمية للتحقق من المعلومات.
جرت مراجعة هذه المقالة علمياً من قِبل: هيئة التحرير العلمية في موسوعة خلية العلمية
آخر تحديث للمقالة: يناير 2026
للتواصل والاستفسارات: صفحة التواصل معنا
العلمية





