رياضيات
-

الجذر التربيعي: من المفهوم الأساسي إلى التطبيقات المعقدة في العلوم الحديثة
يمثل الجذر التربيعي حجر الزاوية في الرياضيات، متجاوزًا كونه مجرد عملية حسابية إلى أداة أساسية في فهم العالم من حولنا.…
أكمل القراءة » -
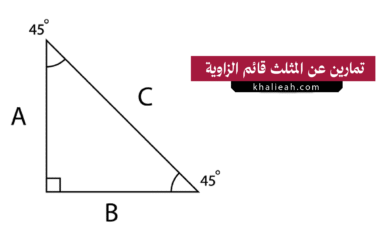
تمارين ومسائل محلولة عن المثلث قائم الزاوية
التمرين الأول: إيجاد طول الوتر (باستخدام نظرية فيثاغورس) المسألة:مثلث (ABC) قائم الزاوية في (B). إذا كان طول الضلع (AB) =…
أكمل القراءة » -
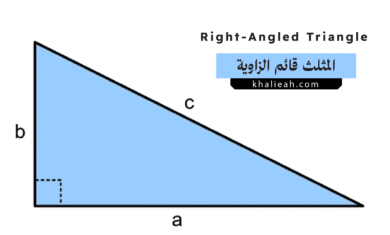
المثلث قائم الزاوية: خصائصه، نظرياته، وتطبيقاته الشاملة
يشكل المثلث قائم الزاوية حجر أساس في الهندسة الإقليدية، وبوابة نحو فهم أعمق لعلم المثلثات وتطبيقاته الواسعة. هذا الشكل البسيط،…
أكمل القراءة » -

جيب التمام: من المثلث القائم إلى موجات الكون وأبعاد البيانات
في قلب الرياضيات والهندسة، تتربع دالة أساسية لا غنى عنها، وهي دالة جيب التمام. هذه الدالة تتجاوز حدود المثلثات لتصف…
أكمل القراءة » -

الجيب: من تعريف المثلث القائم إلى تطبيقاته في الفيزياء والهندسة
تعتبر دالة الجيب حجر الزاوية في علم المثلثات والتحليل الرياضي. فهم هذه الدالة يفتح الأبواب لاستيعاب العديد من الظواهر الطبيعية…
أكمل القراءة » -

نهاية التابع (lim): من المفهوم الحدسي إلى الدقة الرياضية وتطبيقاتها
يمثل مفهوم النهاية حجر الزاوية في التحليل الرياضي الحديث. فهو الجسر الذي يعبر بنا من الجبر التقليدي إلى عوالم حساب…
أكمل القراءة » -

قاعدة لوبيتال: الأداة الحاسمة لحل النهايات والصيغ غير المحددة
في عالم حساب التفاضل والتكامل، تبرز أدوات معينة كحلول أنيقة للمشكلات المعقدة. ومن بين هذه الأدوات، تتألق قاعدة لوبيتال كمنارة…
أكمل القراءة » -

الثابت: من الرياضيات إلى الفيزياء والفلسفة
في سعي الإنسان الدؤوب لفهم العالم، يبرز البحث عن النقاط المرجعية الراسخة كغاية أساسية. ففي خضم التغير والتدفق، يمثل اليقين…
أكمل القراءة » -

المتغير: من المجهول الرياضي إلى حجر الزاوية في العلوم والبرمجة
في نسيج المعرفة البشرية، تقف بعض المفاهيم كأساس لا غنى عنه لتطور الفكر المنطقي والتحليلي. من بين هذه المفاهيم، يبرز…
أكمل القراءة » -

الأعداد المركبة: استكشاف المجال اللامتناهي للدالة الأسية المركبة
تُعتبر الأعداد المركبة حجر الزاوية في العديد من فروع الرياضيات الحديثة والفيزياء والهندسة. لقد أدى ظهورها إلى حل معضلات رياضية استعصت على…
أكمل القراءة »
