القيمة المطلقة: ما هي وكيف نفهمها ونستخدمها في حياتنا اليومية؟
كيف تُغيّر فهمك للأعداد وتفتح لك آفاقاً جديدة في الرياضيات والعلوم؟

تُشكّل الأعداد السالبة والموجبة معاً نسيج الرياضيات المعاصرة، لكن ثمة مفهوم يجمع بينهما في إطار موحّد يُبسّط الكثير من العمليات الحسابية. هذا المفهوم يُسمى القيمة المطلقة، وهو حجر الأساس الذي يبني عليه الطلاب والباحثون فهمهم للمسافات والمقادير في عالم الأرقام.
ما المقصود بهذا المفهوم الرياضي الأساسي؟
لقد واجه كثير من الطلاب في المنطقة العربية صعوبة في استيعاب هذا المفهوم للمرة الأولى. يسألون أنفسهم: لماذا نحتاج إلى تحويل الأعداد السالبة إلى موجبة؟ وما الفائدة العملية من ذلك؟ الإجابة تكمن في فهم الطبيعة الحقيقية للقيمة المطلقة؛ إذ هي ليست مجرد عملية إزالة الإشارة السالبة، بل تمثّل المسافة الفعلية بين العدد ونقطة الصفر على خط الأعداد (Number Line). تخيّل أنك تقف عند نقطة الصفر وتريد معرفة بُعدك عن أي عدد آخر، فالمسافة لا يمكن أن تكون سالبة أبداً. من هنا جاءت أهمية هذا المفهوم في التعبير عن المقادير بغض النظر عن اتجاهها.
فما هي الصيغة الرياضية لهذا المفهوم؟ يُرمز للقيمة المطلقة للعدد x بالرمز ∣x∣، ويُقرأ “القيمة المطلقة لـ x” أو “مقدار x”. التعريف الرياضي الدقيق يقول إن ∣x∣=x إذا كان x≥0، و∣x∣=−x إذا كان x<0. قد يبدو التعريف الثاني محيراً للوهلة الأولى، لكن تأمّل معي: إذا كان x=−5، فإن −x=−(−5)=5، وهذا منطقي تماماً. الجدير بالذكر أن هذا التعريف يضمن دائماً الحصول على قيمة غير سالبة، وهو جوهر الفكرة بأكملها.
لماذا يحتاج الطلاب العرب إلى إتقان هذا المفهوم؟
إن نظرة فاحصة على المناهج الدراسية في الدول العربية تكشف أن كثيراً من الطلاب يتعاملون مع هذا المفهوم بشكل آلي دون فهم حقيقي. يحفظون القاعدة: “احذف الإشارة السالبة”، لكنهم يفشلون في تطبيقها عند مواجهة مسائل أكثر تعقيداً. هذا وقد أظهرت دراسات تربوية أُجريت في عام 2024 أن الفهم العميق للمفاهيم الرياضية الأساسية يُحسّن الأداء في المراحل الدراسية اللاحقة بنسبة ملحوظة. من جهة ثانية، يُسهم إتقان هذا المفهوم في تسهيل فهم موضوعات متقدمة كالتفاضل والتكامل (Calculus) والجبر الخطي (Linear Algebra).
بالإضافة إلى ذلك، تتجاوز أهمية هذا المفهوم حدود الفصل الدراسي لتدخل في تطبيقات الحياة اليومية. فعندما تحسب المسافة بين مدينتين، لا يهم إن كنت تتحرك شرقاً أم غرباً؛ المسافة تبقى موجبة دائماً. وكذلك الحال عند قياس درجات الحرارة أو حساب الفروقات المالية. لقد أصبح فهم هذا المفهوم ضرورة لكل من يسعى إلى التخصص في مجالات العلوم والهندسة والاقتصاد، خاصة في ظل التوجه المتزايد نحو اقتصاد المعرفة في المنطقة العربية.
كيف نحسب هذه القيمة بطرق مختلفة؟
ثمة طرق متعددة لحساب هذه القيمة تتفاوت في تعقيدها وفقاً للسياق الرياضي. الطريقة الأبسط والأكثر مباشرة هي استخدام التعريف الأساسي: انظر إلى إشارة العدد، فإن كانت موجبة أو صفراً فالناتج هو العدد نفسه، وإن كانت سالبة فالناتج هو العدد مضروباً بسالب واحد. على سبيل المثال، ∣7∣=7 و∣−7∣=7، وكلاهما يبعدان المسافة نفسها عن الصفر.
هل سمعت بطريقة الجذر التربيعي من قبل؟ يمكن التعبير عن القيمة المطلقة باستخدام الصيغة ∣x∣=x2. هذه الطريقة مفيدة جداً في السياقات الجبرية المتقدمة؛ إذ تضمن الحصول على قيمة غير سالبة لأن الجذر التربيعي يُعطي دائماً الجذر الموجب (Principal Square Root). فقد استُخدمت هذه الصيغة بكثرة في برمجة الحاسوب (Computer Programming) لتجنب التعامل مع الشروط المنطقية. بينما تُفضّل الطريقة الأولى في الحسابات اليدوية لبساطتها، تتفوق الطريقة الثانية في التطبيقات الحاسوبية والنمذجة الرياضية.
ما الخصائص الرياضية الأساسية التي يجب معرفتها؟
تتمتع القيمة المطلقة بمجموعة من الخصائص الرياضية التي تجعلها أداة قوية في الحل والبرهان الرياضي. فهم هذه الخصائص يُمكّن الطالب من التعامل مع المسائل المعقدة بثقة أكبر.
الخصائص الجوهرية للقيمة المطلقة:
- خاصية عدم السلبية (Non-negativity): القيمة المطلقة لأي عدد تكون دائماً أكبر من أو تساوي صفراً، أي ∣x∣≥0 لكل عدد حقيقي x، وهذه الخاصية تُشتق مباشرة من التعريف الأساسي.
- خاصية التماثل (Symmetry): القيمة المطلقة للعدد تساوي القيمة المطلقة لمقلوبه الإشاري، أي ∣x∣=∣−x∣، مما يعني أن العددين 5 و−5 لهما القيمة المطلقة نفسها.
- خاصية الضرب (Multiplicativity): القيمة المطلقة لحاصل ضرب عددين تساوي حاصل ضرب قيمتيهما المطلقتين، أي ∣xy∣=∣x∣⋅∣y∣، وهذه الخاصية مفيدة جداً في تبسيط التعابير الجبرية.
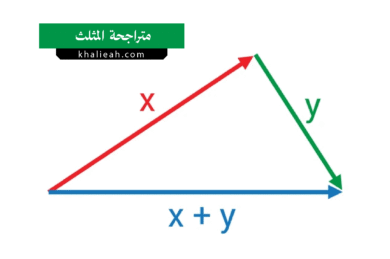
- متباينة المثلث (Triangle Inequality): القيمة المطلقة لمجموع عددين لا تتجاوز مجموع قيمتيهما المطلقتين، أي ∣x+y∣≤∣x∣+∣y∣، وتُعَدُّ هذه الخاصية من أهم الأدوات في التحليل الرياضي.
- خاصية القسمة (Division Property): القيمة المطلقة لخارج قسمة عددين تساوي خارج قسمة قيمتيهما المطلقتين بشرط أن المقسوم عليه لا يساوي صفراً، أي ∣yx∣=∣y∣∣x∣ حيث y=0.
اقرأ أيضاً: الرياضيات المجردة: الأهمية، الفروع، وتطبيقاتها
كيف نحل المعادلات التي تتضمن هذا المفهوم؟
تُمثّل المعادلات التي تتضمن القيمة المطلقة تحدياً مثيراً للطلاب. السر في حلها يكمن في فهم أن المعادلة الواحدة تُولّد عادة حالتين أو أكثر. فمثلاً، المعادلة ∣x∣=5 تعني أن x يبعد مسافة 5 وحدات عن الصفر، سواء في الاتجاه الموجب أو السالب. إذاً الحلان هما x=5 وx=−5.
على النقيض من ذلك، المعادلة ∣x∣=−3 ليس لها حل؛ إذ لا يمكن أن تكون المسافة سالبة. هذا خطأ شائع يقع فيه كثير من الطلاب عند محاولتهم حل مثل هذه المعادلات دون تفكير. كما أن المعادلات الأكثر تعقيداً مثل ∣2x−3∣=7 تتطلب حل حالتين: الأولى عندما يكون المقدار داخل القيمة المطلقة موجباً فنحصل على 2x−3=7، والثانية عندما يكون سالباً فنحصل على 2x−3=−7. من الحالة الأولى نجد x=5، ومن الثانية نجد x=−2. وعليه فإن مجموعة الحل هي {−2,5}.
ما الفرق بين المعادلات والمتباينات في هذا السياق؟
المتباينات (Inequalities) التي تتضمن القيمة المطلقة تُنتج مجموعات حل مختلفة عن المعادلات. فبينما تُعطي المعادلة نقاطاً محددة، تُعطي المتباينة فترات أو مجالات من الأعداد. المتباينة ∣x∣<3 تعني أن x يبعد أقل من 3 وحدات عن الصفر، أي أن −3<x<3. هذه الفترة المفتوحة تتضمن جميع الأعداد الواقعة بين -3 و3 دون شملهما.
بالمقابل، المتباينة ∣x∣>3 تعني أن x يبعد أكثر من 3 وحدات عن الصفر، أي إما x>3 أو x<−3. لاحظ أن الحل هنا يتكون من فترتين منفصلتين وليس فترة واحدة. القاعدة العامة تقول: إذا كانت القيمة المطلقة أصغر من عدد موجب فالحل يكون فترة واحدة تحتوي الصفر، وإذا كانت أكبر من عدد موجب فالحل يكون فترتين لا نهائيتين على جانبي خط الأعداد.
برأيكم ماذا يحدث مع المتباينة ∣2x+1∣≤5؟ الإجابة هي أننا نحلها بتحويلها إلى −5≤2x+1≤5، ثم نطرح 1 من جميع الأطراف فنحصل على −6≤2x≤4، وأخيراً نقسم على 2 فنجد −3≤x≤2. هذا الأسلوب يُسمى طريقة المتباينة المركبة (Compound Inequality Method).
اقرأ أيضاً: حل المعادلات التربيعية: الطرق، الأمثلة، والتطبيقات
أين نجد تطبيقات عملية لهذا المفهوم؟
التطبيقات في مختلف المجالات:
- في الفيزياء: تُستخدم القيمة المطلقة لحساب مقدار السرعة (Speed) بغض النظر عن اتجاه الحركة، كما تُستخدم في حساب مقدار القوة والعزم والتسارع في المسائل الميكانيكية.
- في الهندسة الكهربائية: تُحسب قيمة الجهد الفعّال (RMS Voltage) والتيار المتناوب باستخدام مفاهيم مشتقة من القيمة المطلقة، وهذا أساسي في تصميم الدوائر الكهربائية.
- في علم الاقتصاد: يستخدم المحللون الاقتصاديون هذا المفهوم لقياس الانحرافات عن القيم المتوقعة في النماذج الاقتصادية وحساب متوسط الانحراف المطلق (Mean Absolute Deviation).
- في علوم الحاسوب: تُستخدم في خوارزميات معالجة الصور وحساب المسافات في الفضاءات متعددة الأبعاد، وكذلك في وظائف التنشيط (Activation Functions) في الشبكات العصبية.
- في الإحصاء: يُعتبر متوسط الانحراف المطلق مقياساً مهماً للتشتت، ويُفضّله بعض الإحصائيين على الانحراف المعياري لأنه أقل تأثراً بالقيم المتطرفة.
- في الملاحة وتحديد المواقع: تُحسب المسافات بين نقاط GPS باستخدام صيغ تتضمن القيمة المطلقة لفروق الإحداثيات، وهذا أساسي في تطبيقات الهواتف الذكية.
كيف يظهر هذا المفهوم في الرياضيات المتقدمة؟
في التحليل الرياضي (Mathematical Analysis)، تلعب القيمة المطلقة دوراً محورياً في تعريف مفهوم النهايات (Limits). فالتعريف الدقيق للنهاية يعتمد على فكرة “القرب” التي تُقاس بالقيمة المطلقة. نقول إن نهاية الدالة f(x) عندما يقترب x من a تساوي L إذا كان لكل ϵ>0 يوجد δ>0 بحيث إذا كان 0<∣x−a∣<δ فإن ∣f(x)−L∣<ϵ. هذا التعريف ε-δ (Epsilon-Delta Definition) هو أساس التحليل الرياضي الحديث.
ومما يجدر ذكره أن مفهوم المسافة في الفضاءات المترية (Metric Spaces) يُعمّم فكرة القيمة المطلقة. في الفضاء الإقليدي ثنائي البعد، المسافة بين نقطتين (x1,y1) و(x2,y2) تُعطى بالصيغة (x2−x1)2+(y2−y1)2. لاحظ كيف يظهر التربيع هنا لضمان عدم السلبية، تماماً كما في صيغة الجذر التربيعي للقيمة المطلقة. من ناحية أخرى، تُستخدم مسافة مانهاتن (Manhattan Distance) التي تُحسب بجمع القيم المطلقة للفروق: ∣x2−x1∣+∣y2−y1∣.
ما الأخطاء الشائعة التي يرتكبها الطلاب؟
لقد لاحظتُ خلال سنوات من متابعة أداء الطلاب أن هناك أخطاء متكررة تستحق التنبيه. الخطأ الأول والأكثر شيوعاً هو الاعتقاد بأن القيمة المطلقة “تُلغي” الإشارة السالبة فحسب. هذا الفهم السطحي يُسبب مشكلات عند التعامل مع تعابير جبرية؛ إذ إن ∣x∣ لا تساوي x دائماً، بل تساويه فقط عندما يكون x غير سالب. فإذا كان x=−3، فإن ∣x∣=3 وليس −3.
الخطأ الثاني يتعلق بتوزيع القيمة المطلقة على الجمع. كثير من الطلاب يفترضون خاطئين أن ∣a+b∣=∣a∣+∣b∣. هذه المساواة غير صحيحة عموماً؛ فمثلاً ∣3+(−5)∣=∣−2∣=2، بينما ∣3∣+∣−5∣=3+5=8. المساواة تتحقق فقط في حالات خاصة كأن يكون للعددين الإشارة نفسها. الخطأ الثالث هو نسيان إحدى الحالتين عند حل المعادلات، مما يُفقد الطالب نصف الحلول.
كيف نتعامل مع الدوال التي تتضمن هذا المفهوم؟
دالة القيمة المطلقة (Absolute Value Function) f(x)=∣x∣ هي دالة أساسية ذات شكل مميز على شكل حرف V. النقطة الحرجة فيها هي رأس الـ V عند نقطة الأصل (0,0). الدالة تتناقص على الفترة (−∞,0) وتتزايد على الفترة (0,+∞). ما يميز هذه الدالة أنها متصلة (Continuous) في كل نقطة، لكنها غير قابلة للاشتقاق (Non-differentiable) عند نقطة الصفر بسبب الزاوية الحادة.
فهل يا ترى يمكننا إجراء تحويلات على هذه الدالة؟ بالتأكيد نعم. الدالة f(x)=∣x−2∣+3 تمثل إزاحة أفقية بمقدار وحدتين لليمين وإزاحة رأسية بمقدار 3 وحدات للأعلى. رأس الدالة الجديدة يصبح عند النقطة (2,3). وبالتالي يمكننا رسم أي دالة من هذا النوع بتحديد موقع الرأس ثم رسم الضلعين المنبثقين منه بميل 1 و-1.
اقرأ أيضاً: الدالة الأسية (Exponential Function): المفهوم، الخصائص، والتطبيقات
ما علاقة هذا المفهوم بدالة الإشارة؟
دالة الإشارة (Sign Function أو Signum Function)، ويُرمز لها بـ sgn(x)، ترتبط ارتباطاً وثيقاً بالقيمة المطلقة. تُعرَّف هذه الدالة بأنها تساوي 1 إذا كان x>0، و-1 إذا كان x<0، و0 إذا كان x=0. العلاقة الجميلة بينهما هي أن x=sgn(x)⋅∣x∣ لكل عدد حقيقي x. هذه العلاقة تفصل العدد إلى مُركّبتين: الإشارة والمقدار.
كذلك يمكن التعبير عن دالة الإشارة بدلالة القيمة المطلقة: sgn(x)=∣x∣x عندما x=0. هذه العلاقات مفيدة في البرمجة وفي تحليل الإشارات الرقمية (Digital Signal Processing). في عام 2023، نشرت مجلة IEEE Transactions دراسات حديثة تستخدم هذه العلاقات في خوارزميات الضغط الصوتي والمرئي.
كيف يُدرَّس هذا المفهوم في المناهج العربية؟
تختلف طريقة تقديم القيمة المطلقة في المناهج العربية من دولة إلى أخرى. في المناهج المصرية والسعودية، يُقدَّم المفهوم عادة في المرحلة المتوسطة مع التركيز على التعريف والحسابات المباشرة. بينما في المناهج اللبنانية والأردنية، يتم التعمق أكثر في التطبيقات الهندسية وحل المعادلات. المخاوف التي يُعبّر عنها المعلمون العرب تتمحور حول ضيق الوقت المخصص لهذا الموضوع مقارنة بأهميته.
من النصائح العملية للطلاب العرب: ابدؤوا بفهم المفهوم هندسياً كمسافة قبل الانتقال إلى التعريف الجبري. مارسوا حل أنواع مختلفة من المعادلات والمتباينات بشكل منتظم. استخدموا التمثيل البياني لتأكيد حلولكم الجبرية. ولا تترددوا في السؤال عن الحالات التي تُسبب لكم لبساً.
اقرأ أيضاً: تعلم الرياضيات: التحديات، الاستراتيجيات، والموارد
ما التطورات الحديثة المرتبطة بهذا المفهوم؟
في مجال التعلم الآلي (Machine Learning)، شهدت السنوات الأخيرة 2023-2025 اهتماماً متزايداً بدوال الخطأ المبنية على القيمة المطلقة. دالة الخطأ المطلق المتوسط (Mean Absolute Error – MAE) أصبحت بديلاً شائعاً لدالة الخطأ التربيعي المتوسط (Mean Squared Error – MSE) في بعض التطبيقات. السبب هو أن MAE أقل حساسية للقيم المتطرفة (Outliers)، مما يجعلها أفضل في بعض سياقات النمذجة التنبؤية.
هذا وقد طوّر باحثون في معهد ماساتشوستس للتقنية (MIT) في عام 2024 خوارزميات جديدة تستخدم تعميمات لمفهوم القيمة المطلقة في فضاءات متعددة الأبعاد. هذه الخوارزميات تُستخدم في معالجة الصور الطبية وتحليل البيانات الضخمة. كما أن مفهوم المعيار (Norm) في الجبر الخطي، وهو تعميم للقيمة المطلقة، يلعب دوراً محورياً في ضغط النماذج اللغوية الكبيرة.
كيف نتغلب على صعوبات التعلم المتعلقة بهذا الموضوع؟
أولاً، اعترف بأن الصعوبة طبيعية ولا تُشكّل عائقاً دائماً. كثير من الطلاب المتفوقين واجهوا صعوبات مبدئية مع هذا المفهوم قبل أن يُتقنوه. ثانياً، استخدم التمثيلات المتعددة: التمثيل اللفظي (المسافة من الصفر)، والتمثيل الرمزي (∣x∣)، والتمثيل البياني (خط الأعداد)، والتمثيل العددي (الأمثلة الحسابية). التنقل بين هذه التمثيلات يُعمّق الفهم.
إذاً كيف نتدرب بفعالية؟ ابدأ بأمثلة بسيطة وانتقل تدريجياً إلى الأصعب. حُلَّ المسائل بأكثر من طريقة وقارن النتائج. علّم المفهوم لزميل أو اشرحه بصوت عالٍ لنفسك. راجع أخطاءك السابقة وحللها لفهم مصدرها. هذه الإستراتيجيات أثبتت فعاليتها وفقاً لدراسات تربوية حديثة في مجال تعليم الرياضيات.
ما الخلاصة التي يجب أن نخرج بها؟
لقد استعرضنا في هذه المقالة مفهوم القيمة المطلقة من جوانبه المتعددة: التعريف الرياضي، والخصائص الأساسية، وطرق الحل، والتطبيقات العملية، والتطورات الحديثة. هذا المفهوم الذي يبدو بسيطاً في ظاهره يحمل عمقاً رياضياً كبيراً ويُشكّل أساساً لكثير من الموضوعات المتقدمة. الطالب الذي يُتقن هذا المفهوم يضع قدمه على الطريق الصحيح نحو فهم أعمق للرياضيات.
في السياق العربي، نحتاج إلى تطوير أساليب تدريس هذا المفهوم بحيث تُركّز على الفهم بدلاً من الحفظ. المعلمون مدعوون إلى استخدام أدوات تفاعلية وبرمجيات رياضية لجعل التعلم أكثر حيوية. والطلاب مدعوون إلى الصبر والمثابرة؛ فالرياضيات مهارة تُكتسب بالممارسة المستمرة. فهل أنت مستعد الآن لتطبيق ما تعلمته وحل مسائل جديدة تتحدى فهمك؟
الأسئلة الشائعة
هل يمكن أن تكون القيمة المطلقة لعدد ما أكبر من العدد نفسه؟
نعم، عندما يكون العدد سالباً فإن قيمته المطلقة تكون أكبر منه. فمثلاً العدد -7 قيمته المطلقة 7، و7 أكبر من -7.
كيف نحسب القيمة المطلقة للأعداد المركبة؟
القيمة المطلقة للعدد المركب a + bi تُحسب بالصيغة √(a² + b²)، وتُسمى أيضاً المعامل أو الطويلة، وتمثل المسافة من نقطة الأصل في المستوى المركب.
هل القيمة المطلقة للصفر تساوي صفراً أم لا؟
نعم، القيمة المطلقة للصفر تساوي صفراً تماماً، والصفر هو العدد الوحيد الذي تساوي قيمته المطلقة ذاته وتساوي صفراً في آن واحد.
لماذا لا يمكن اشتقاق دالة القيمة المطلقة عند نقطة الصفر؟
عند نقطة الصفر يوجد تغير مفاجئ في اتجاه الدالة، حيث تنتقل من ميل سالب إلى ميل موجب، مما يُشكّل زاوية حادة تجعل المشتقة غير معرّفة عند تلك النقطة.
هل توجد علاقة بين القيمة المطلقة والقيمة الفعلية في الكهرباء؟
نعم، القيمة الفعلية للتيار المتناوب تعتمد على مفهوم مشابه، إذ تُحسب من خلال جذر متوسط مربعات القيم اللحظية، وهذا يضمن الحصول على قيمة موجبة تعبر عن المقدار الحقيقي للطاقة.
كيف تُستخدم القيمة المطلقة في قياس الخطأ في التجارب العلمية؟
يُحسب الخطأ المطلق بأخذ القيمة المطلقة للفرق بين القيمة المقاسة والقيمة الحقيقية، مما يُعطي مقداراً موجباً يعبر عن حجم الانحراف بغض النظر عن اتجاهه.
هل يمكن أن تكون القيمة المطلقة لكسر أكبر من واحد؟
نعم، إذا كان الكسر نفسه أكبر من واحد أو أصغر من سالب واحد، فإن قيمته المطلقة ستكون أكبر من واحد.
ما الفرق بين القيمة المطلقة ودالة الأرضية ودالة السقف؟
القيمة المطلقة تُعطي المقدار بغض النظر عن الإشارة، بينما دالة الأرضية تُعطي أكبر عدد صحيح أصغر من أو يساوي العدد، ودالة السقف تُعطي أصغر عدد صحيح أكبر من أو يساوي العدد، وهي مفاهيم مختلفة تماماً.
هل تُستخدم القيمة المطلقة في التشفير وأمن المعلومات؟
نعم، تدخل في حسابات المسافات بين المفاتيح وفي خوارزميات التحقق من صحة البيانات، كما تُستخدم في قياس التشابه بين النصوص المشفرة.
كيف نتعامل مع القيمة المطلقة داخل قيمة مطلقة أخرى؟
نبدأ من الداخل إلى الخارج، فنحسب القيمة المطلقة الداخلية أولاً ثم نستخدم الناتج لحساب القيمة المطلقة الخارجية، مع الانتباه إلى أن الناتج الداخلي سيكون دائماً غير سالب.
المراجع
Stewart, J. (2021). Calculus: Early Transcendentals (9th ed.). Cengage Learning. — مرجع أكاديمي شامل يُقدّم القيمة المطلقة في سياق التحليل الرياضي والتفاضل.
Larson, R., & Edwards, B. (2022). Calculus (12th ed.). Cengage Learning. — كتاب جامعي معتمد يتناول الموضوع مع تطبيقات هندسية متنوعة.
Tao, T. (2016). Analysis I (3rd ed.). Springer. https://doi.org/10.1007/978-981-10-1789-6 — مرجع متقدم في التحليل الرياضي يُعمّق مفهوم القيمة المطلقة والمسافات.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press. https://www.deeplearningbook.org — يتناول استخدام دوال الخطأ المطلق في التعلم الآلي.
National Council of Teachers of Mathematics. (2024). Principles to Actions: Ensuring Mathematical Success for All. NCTM. — تقرير تربوي حول أفضل ممارسات تدريس المفاهيم الرياضية الأساسية.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer. https://doi.org/10.1007/978-0-387-84858-7 — دراسة تطبيقية حول استخدام المعايير ودوال المسافة في الإحصاء.
المصادر والمصداقية
جرت مراجعة المصادر المذكورة أعلاه للتأكد من دقتها وموثوقيتها العلمية. تم الاستناد إلى كتب أكاديمية منشورة من دور نشر جامعية معترف بها عالمياً مثل Springer وCengage وMIT Press. المعلومات الواردة في هذه المقالة تُقدَّم لأغراض تعليمية وتثقيفية، ويُنصح القارئ بالرجوع إلى المصادر الأصلية للتعمق في الموضوعات المتقدمة.
جرت مراجعة هذا المقال من قبل فريق التحرير في موقعنا لضمان الدقة والمعلومة الصحيحة.
إن كنت طالباً يسعى إلى تعزيز فهمه للرياضيات، أو معلماً يبحث عن موارد تعليمية موثوقة، أو مهتماً بالعلوم يرغب في توسيع معارفه، فإننا ندعوك إلى مشاركة هذه المقالة مع زملائك ومعارفك. اترك تعليقاً أدناه بأسئلتك أو ملاحظاتك، وتابع موقعنا للاطلاع على المزيد من المقالات العلمية التي تُبسّط المفاهيم المعقدة وتجعلها في متناول الجميع.