الانحراف المعياري: كيف نفهم تشتت البيانات بطريقة مبسطة؟

عندما نتعامل مع الأرقام في حياتنا اليومية، لا يكفي أن نعرف المتوسط الحسابي فقط، بل نحتاج لفهم كيف تتوزع هذه الأرقام حول ذلك المتوسط. إن مقاييس التشتت توفر لنا نظرة أعمق لطبيعة البيانات وتساعدنا على اتخاذ قرارات أكثر دقة في مجالات متعددة من العلوم والأعمال والحياة اليومية.

مقدمة

لقد واجهت موقفاً مثيراً خلال عملي كمدرس للإحصاء قبل سنوات؛ إذ سألني أحد الطلاب: “لماذا نحتاج للانحراف المعياري إذا كان لدينا المتوسط الحسابي؟”. هذا السؤال البسيط فتح باباً واسعاً لمناقشة عميقة حول أهمية فهم تشتت البيانات. تخيل معي فريقين رياضيين لهما نفس المتوسط في عدد الأهداف، لكن الفريق الأول يسجل أهدافاً بشكل منتظم بينما الفريق الثاني متقلب الأداء. هنا يظهر دور مقاييس التشتت في الكشف عن الفروقات الحقيقية بين المجموعات.

إن علم الإحصاء يمنحنا أدوات قوية لفهم الواقع من حولنا، ومن أبرز هذه الأدوات التباين (Variance) ومقياس الانحراف المعياري (Standard Deviation). فقد أصبحت هذه المفاهيم أساسية في مختلف المجالات من الطب إلى الاقتصاد، ومن الهندسة إلى العلوم الاجتماعية. بالإضافة إلى ذلك، فإن فهمها يساعدنا في تحليل البيانات التي نواجهها يومياً واتخاذ قرارات مبنية على أساس علمي سليم.

ما المقصود بتشتت البيانات في الإحصاء؟

التشتت (Dispersion) يشير إلى مدى انتشار القيم أو تباعدها عن بعضها البعض في مجموعة بيانات معينة. عندما نقول إن البيانات متشتتة، فهذا يعني أن القيم متباعدة عن بعضها وعن المتوسط الحسابي؛ إذ لا تتركز القيم في نطاق ضيق. كما أن فهم درجة التشتت يكشف لنا عن طبيعة البيانات بشكل أعمق من مجرد معرفة المتوسط.

لنفترض أن لدينا مجموعتين من الطلاب، المجموعة الأولى حصلت على درجات: 48، 49، 50، 51، 52، بينما المجموعة الثانية حصلت على: 20، 35، 50، 65، 80. على النقيض من ذلك، رغم أن كلا المجموعتين لهما نفس المتوسط الحسابي (50)، إلا أن التشتت في المجموعة الثانية أكبر بكثير. هذا الاختلاف في التشتت يعطينا معلومات قيمة عن استقرار الأداء وتجانس المجموعة. بينما تُظهر المجموعة الأولى تجانساً واضحاً في الأداء، تكشف الثانية عن تفاوت كبير بين أفراد المجتمع.

ما هو الانحراف المعياري وكيف يُحسب؟

الانحراف المعياري هو مقياس إحصائي يقيس مقدار تشتت القيم عن المتوسط الحسابي للبيانات. إنه يخبرنا بمتوسط المسافة بين كل قيمة والمتوسط العام، ويُعبر عنه بنفس وحدة قياس البيانات الأصلية. فما هي الخطوات اللازمة لحساب هذا المقياس المهم؟ الإجابة تكمن في فهم العملية الحسابية بطريقة منهجية.

لحساب الانحراف المعياري، نتبع الخطوات التالية بدقة. أولاً، نحسب المتوسط الحسابي لجميع القيم في مجموعة البيانات. ثانياً، نطرح المتوسط من كل قيمة على حدة لنحصل على الانحرافات الفردية. ثالثاً، نربع كل انحراف من هذه الانحرافات لتجنب القيم السالبة ولإعطاء وزن أكبر للقيم البعيدة عن المتوسط. رابعاً، نجمع مربعات الانحرافات ونقسمها على عدد القيم (أو عدد القيم ناقص واحد في حالة العينة). أخيراً، نأخذ الجذر التربيعي للناتج للحصول على الانحراف المعياري. وبالتالي، فإن العملية تتطلب دقة في التطبيق لكنها ليست معقدة بالضرورة.

كيف يرتبط التباين بالانحراف المعياري؟

التباين (Variance) يُعَدُّ الخطوة السابقة مباشرة قبل الحصول على الانحراف المعياري، وهو متوسط مربعات الانحرافات عن المتوسط الحسابي. من ناحية أخرى، الانحراف المعياري هو ببساطة الجذر التربيعي للتباين. إذاً كيف نفهم هذه العلاقة الرياضية بطريقة عملية؟ العلاقة وثيقة جداً، ويمكن القول إن كلا المقياسين يعبران عن نفس الفكرة لكن بطرق مختلفة.

عندما نحسب التباين، نحصل على قيمة بوحدة قياس مربعة (مثل متر مربع أو درجة مربعة)، مما يجعل تفسيرها أصعب في السياق العملي. لقد وجدت خلال سنوات تدريسي أن الطلاب يجدون صعوبة في فهم معنى “درجة مربعة” عند قياس الأداء الأكاديمي. وعليه فإن الانحراف المعياري يحل هذه المشكلة بأخذ الجذر التربيعي، فنعود إلى الوحدة الأصلية للبيانات. هذا وقد جعل الانحراف المعياري أكثر شيوعاً واستخداماً في التطبيقات العملية، فهو أسهل في الفهم والتفسير للأشخاص غير المتخصصين في الإحصاء.

ما الفرق بين الانحراف المعياري للعينة والمجتمع؟

الفروق الأساسية في المفاهيم والرموز

الانحراف المعياري للمجتمع (Population Standard Deviation) يُرمز له بالرمز اليوناني σ (سيجما)، ويُحسب عندما تكون لدينا بيانات كاملة عن جميع أفراد المجتمع الإحصائي. بالمقابل، الانحراف المعياري للعينة (Sample Standard Deviation) يُرمز له بالحرف اللاتيني s، ويُستخدم عندما نعمل مع عينة فقط من المجتمع. الفرق الجوهري بين الاثنين يكمن في المعادلة المستخدمة والهدف من كل منهما.

في الحسابات العملية، نستخدم للمجتمع القسمة على العدد الكلي للقيم (N)، بينما نقسم على (n-1) في حالة العينة، حيث n هو عدد أفراد العينة. لماذا هذا الاختلاف؟ لأن العينة عادة ما تُقلل من تقدير التشتت الحقيقي في المجتمع، فنستخدم (n-1) لتصحيح هذا التحيز وللحصول على تقدير أكثر دقة. كما أن هذا التصحيح يُعرف بتصحيح بيسل (Bessel’s Correction)، وهو مفهوم مهم في الإحصاء الاستدلالي.

الاختيار الصحيح في التطبيقات العملية

عندما تدرس جميع طلاب مدرسة معينة، فأنت تدرس المجتمع الكامل وتستخدم σ. على النقيض من ذلك، إذا اخترت عينة عشوائية من طلاب مدينة كاملة، فأنت تعمل مع عينة وتستخدم s. الاختيار بين المعادلتين ليس اعتباطياً، بل يعتمد على طبيعة البيانات المتاحة والهدف من التحليل.

في معظم البحوث العلمية والدراسات الميدانية، نعمل مع عينات وليس مجتمعات كاملة؛ إذ يصعب أو يستحيل الوصول إلى كل فرد في المجتمع. وبالتالي، فإن الانحراف المعياري للعينة هو الأكثر استخداماً في التطبيقات العملية. الجدير بالذكر أن البرامج الإحصائية الحديثة مثل SPSS وExcel توفر دوال مختلفة لحساب كل نوع، فيجب على الباحث أن يختار الدالة المناسبة وفقاً لطبيعة بياناته.

متى نستخدم الانحراف المعياري في الحياة العملية؟

في مجال المال والاستثمار، يُستخدم الانحراف المعياري لقياس مخاطر الأصول المالية والمحافظ الاستثمارية. انظر إلى سوق الأسهم، حيث يشير انحراف معياري عالٍ إلى تقلبات كبيرة في أسعار الأسهم، مما يعني مخاطر أكبر وربما فرص ربح أكبر أيضاً. فقد يستخدم المستثمرون هذا المقياس لتحديد مستوى المخاطرة الذي يرغبون في تحمله، ولبناء محافظ استثمارية متوازنة.

في المجال الطبي والصحي، يساعد الانحراف المعياري في فهم التوزيعات الطبيعية للقياسات الحيوية مثل ضغط الدم، ومستوى السكر، ومؤشر كتلة الجسم. كما أن الأطباء يستخدمونه لتحديد ما إذا كانت قراءة معينة طبيعية أم خارجة عن المعدل المعتاد. بالإضافة إلى ذلك، في مراقبة الجودة الصناعية، تعتمد المصانع على الانحراف المعياري لضمان تجانس المنتجات والحفاظ على معايير الجودة. ومما يُذكر أن صناعة الأدوية تستخدمه بشكل مكثف لضمان تركيز دقيق ومتسق للمواد الفعالة.

لماذا يُعَدُّ الانحراف المعياري أكثر شيوعاً من التباين؟

السبب الأول والأكثر أهمية هو أن الانحراف المعياري يُعبر عنه بنفس وحدة القياس الأصلية للبيانات. إذا كنت تقيس أوزان أشخاص بالكيلوغرام، فالانحراف المعياري سيكون بالكيلوغرام أيضاً، بينما التباين سيكون بالكيلوغرام المربع. هل سمعت به من قبل أن أحداً يقول “التشتت في الأوزان هو 25 كيلوغرام مربع”؟ هذا التعبير غير عملي وصعب الفهم للشخص العادي.

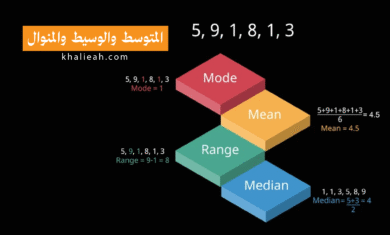
من جهة ثانية، يسهل تفسير الانحراف المعياري في سياق البيانات الفعلية. عندما نقول إن متوسط رواتب الموظفين هو 5000 دولار والانحراف المعياري 500 دولار، نفهم مباشرة أن معظم الرواتب تتراوح بالقرب من هذا النطاق. وكذلك يُستخدم الانحراف المعياري في قاعدة التوزيع الطبيعي الشهيرة: حوالي 68% من البيانات تقع ضمن انحراف معياري واحد من المتوسط، و95% ضمن انحرافين معياريين، و99.7% ضمن ثلاثة انحرافات معيارية. هذه القاعدة تجعل الانحراف المعياري أداة قوية وبديهية لفهم توزيع البيانات.

كيف نفسر قيم الانحراف المعياري بشكل صحيح؟

انحراف معياري صغير (قريب من الصفر) يعني أن القيم متقاربة جداً من بعضها ومن المتوسط الحسابي، مما يشير إلى تجانس عالٍ في البيانات. تخيل مصنعاً ينتج قطعاً معدنية بطول محدد؛ انحراف معياري صغير يعني أن الإنتاج متسق ومتطابق تقريباً، وهذا أمر مرغوب فيه في مراقبة الجودة. بينما انحراف معياري كبير يدل على تشتت واسع وتنوع في القيم، مما قد يكون إيجابياً أو سلبياً حسب السياق.

في بعض المجالات، التشتت الكبير مرغوب ومطلوب. برأيكم ماذا يعني تنوع كبير في أفكار أعضاء فريق عمل إبداعي؟ الإجابة هي أن هذا التنوع قد يؤدي إلى حلول مبتكرة ومنظورات متعددة تثري العمل. على النقيض من ذلك، في مجالات أخرى مثل التصنيع الدقيق أو إعطاء الأدوية، نحتاج لانحراف معياري صغير جداً لضمان الدقة والسلامة. إذاً، لا يمكن الحكم على الانحراف المعياري بأنه “جيد” أو “سيء” بمعزل عن السياق والهدف من التحليل.

الخاتمة

لقد قدمنا في هذه المقالة فهماً شاملاً ومبسطاً لمفهومي التباين والانحراف المعياري، وكيف يساعداننا في فهم تشتت البيانات بطريقة علمية دقيقة. إن إتقان هذين المفهومين يفتح أمامنا آفاقاً واسعة لتحليل البيانات بفعالية في مختلف المجالات، من البحث العلمي إلى اتخاذ القرارات اليومية. كما أن الانحراف المعياري بوجه خاص يُعَدُّ من أكثر المقاييس الإحصائية استخداماً وأهمية في عالمنا المعاصر الذي يعتمد بشكل متزايد على البيانات والتحليل الكمي.

فهل ستبدأ الآن في ملاحظة مقاييس التشتت والانحراف المعياري في التقارير والدراسات التي تقرأها، وتستخدمها لفهم أعمق للبيانات من حولك؟

الأسئلة الشائعة

ما الفرق بين المدى والانحراف المعياري كمقاييس للتشتت؟

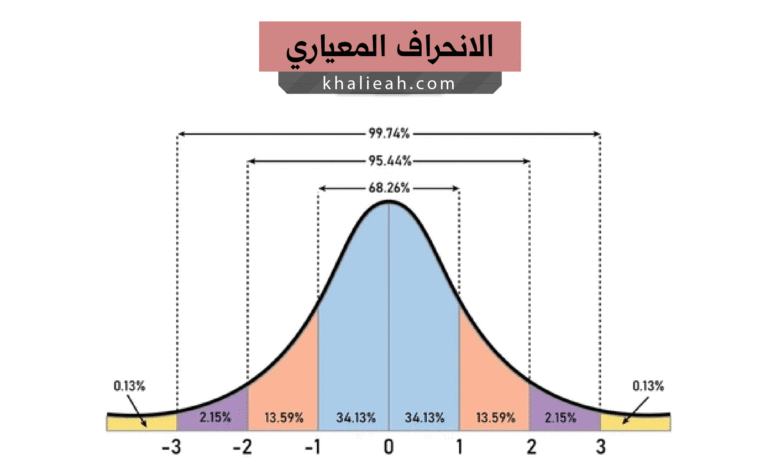
المدى (Range) هو الفرق بين أكبر وأصغر قيمة في مجموعة البيانات، وهو مقياس بسيط لكنه يتأثر بالقيم المتطرفة بشكل كبير. بينما الانحراف المعياري يأخذ في الاعتبار جميع القيم ويقيس متوسط بعد كل قيمة عن المتوسط الحسابي، مما يجعله أكثر دقة وشمولاً في قياس التشتت الفعلي للبيانات. إن المدى قد يكون مضللاً في حالة وجود قيمة شاذة واحدة، بينما الانحراف المعياري يعطي صورة أكثر واقعية عن توزيع البيانات بأكملها.

هل يمكن أن يكون الانحراف المعياري أكبر من المتوسط الحسابي؟

نعم، يمكن أن يكون الانحراف المعياري أكبر من المتوسط الحسابي، وهذا يحدث عندما يكون التشتت في البيانات كبيراً جداً مقارنة بقيمة المتوسط. على سبيل المثال، إذا كانت البيانات تحتوي على قيم متباعدة جداً أو كان المتوسط قريباً من الصفر، فقد يتجاوز الانحراف المعياري قيمة المتوسط. هذا الوضع شائع في البيانات المالية والاقتصادية، حيث يشير إلى مستوى عالٍ من التقلب وعدم الاستقرار في القيم المدروسة.

لماذا نربع الانحرافات عند حساب التباين بدلاً من أخذ القيمة المطلقة؟

التربيع يخدم عدة أغراض مهمة في الحسابات الإحصائية. أولاً، يزيل الإشارات السالبة ويجعل جميع القيم موجبة دون استخدام القيمة المطلقة التي تصعب التعامل معها رياضياً. ثانياً، يعطي وزناً أكبر للانحرافات الكبيرة، مما يجعل المقياس أكثر حساسية للقيم البعيدة عن المتوسط. ثالثاً، التربيع يحافظ على الخصائص الرياضية المفيدة التي تسهل العمليات الإحصائية المتقدمة، كما أن له أساس نظري قوي في نظرية المربعات الصغرى التي تُستخدم في الانحدار والتقدير الإحصائي.

كيف نتعامل مع القيم الشاذة عند حساب الانحراف المعياري؟

القيم الشاذة (Outliers) تؤثر بشكل كبير على الانحراف المعياري لأنها تبتعد كثيراً عن المتوسط، وعند تربيع انحرافاتها يزداد تأثيرها. قبل حساب الانحراف المعياري، يجب فحص البيانات للكشف عن القيم الشاذة باستخدام الرسوم البيانية أو القواعد الإحصائية مثل قاعدة الانحرافات المعيارية الثلاثة. بعد تحديدها، يمكن اتخاذ قرار بإزالتها إذا كانت ناتجة عن خطأ في القياس أو الإدخال، أو الإبقاء عليها إذا كانت تمثل ظاهرة حقيقية. في بعض الحالات، يُفضل استخدام مقاييس تشتت بديلة أقل تأثراً بالقيم الشاذة مثل الانحراف الربيعي (Interquartile Range).

ما علاقة الانحراف المعياري بمنحنى التوزيع الطبيعي؟

في التوزيع الطبيعي (Normal Distribution)، يلعب الانحراف المعياري دوراً محورياً في تحديد شكل المنحنى وانتشاره. القاعدة التجريبية (Empirical Rule) تنص على أن حوالي 68% من البيانات تقع ضمن انحراف معياري واحد من المتوسط، و95% ضمن انحرافين معياريين، و99.7% ضمن ثلاثة انحرافات معيارية. هذه العلاقة تجعل الانحراف المعياري أداة قوية لتحديد احتمالات وقوع القيم المختلفة، ولتحويل البيانات إلى درجات معيارية (Z-scores) التي تسمح بمقارنة قيم من توزيعات مختلفة، كما تُستخدم في اختبارات الفرضيات وفترات الثقة.

هل الانحراف المعياري الصفري ممكن وماذا يعني؟

نعم، الانحراف المعياري يساوي صفراً عندما تكون جميع القيم في مجموعة البيانات متطابقة تماماً. في هذه الحالة، لا يوجد أي تشتت، وكل قيمة تساوي المتوسط الحسابي بالضبط. مثلاً، إذا سجل جميع الطلاب درجة 90 في امتحان ما، فإن الانحراف المعياري سيكون صفراً. هذا الوضع نادر في البيانات الواقعية، لكنه قد يحدث في حالات خاصة مثل البيانات المصطنعة أو القياسات المتكررة لثابت فيزيائي. عملياً، انحراف معياري قريب جداً من الصفر يشير إلى تجانس شبه كامل في البيانات.

كيف يختلف استخدام الانحراف المعياري في البحوث الكمية والنوعية؟

الانحراف المعياري يُستخدم حصرياً في البحوث الكمية التي تتعامل مع بيانات رقمية قابلة للقياس. في هذه البحوث، يساعد على تقييم مدى تمثيل العينة للمجتمع، وتحديد دقة القياسات، واختبار الفرضيات الإحصائية. أما البحوث النوعية فتتعامل مع بيانات وصفية غير رقمية مثل المقابلات والملاحظات، ولا يمكن تطبيق الانحراف المعياري عليها مباشرة. مع ذلك، في بعض البحوث المختلطة التي تجمع بين المنهجين، قد يتم تحويل بعض البيانات النوعية إلى كمية (مثل التقييمات على مقياس ليكرت) ثم حساب الانحراف المعياري لها.

ما أهمية الانحراف المعياري في التحليل المالي وإدارة المخاطر؟

في التحليل المالي، يُعَدُّ الانحراف المعياري مقياساً أساسياً للمخاطر والتقلب (Volatility). يستخدم المستثمرون ومديرو المحافظ الاستثمارية الانحراف المعياري لقياس تذبذب عوائد الأصول المالية؛ فالانحراف المعياري العالي يشير إلى استثمار أكثر خطورة ولكن محتمل عوائد أعلى، بينما الانحراف المعياري المنخفض يدل على استقرار أكبر. كما يُستخدم في حساب نسبة شارب (Sharpe Ratio) التي تقيس العائد المعدل بالمخاطر، وفي نماذج تسعير الأصول، وفي تقييم أداء صناديق الاستثمار. بالإضافة إلى ذلك، يساعد في تحديد التنويع الأمثل للمحفظة وفي اختبارات القيمة المعرضة للخطر (Value at Risk).

كيف تؤثر زيادة حجم العينة على دقة الانحراف المعياري؟

زيادة حجم العينة تؤدي عموماً إلى تقدير أكثر استقراراً ودقة للانحراف المعياري الحقيقي للمجتمع. العينات الصغيرة تكون عرضة للتقلبات العشوائية وقد لا تمثل المجتمع بشكل كافٍ، مما يجعل الانحراف المعياري المحسوب منها أقل موثوقية. مع زيادة حجم العينة، يقترب التوزيع من التوزيع الطبيعي وفقاً لنظرية النهاية المركزية، ويصبح الانحراف المعياري للعينة أقرب إلى الانحراف المعياري الفعلي للمجتمع. لكن هذا لا يعني أن قيمة الانحراف المعياري نفسها ستنخفض بالضرورة؛ بل يعني أن تقديرنا له يصبح أكثر دقة واستقراراً.

ما البدائل المتاحة للانحراف المعياري في قياس التشتت؟

توجد عدة بدائل للانحراف المعياري، كل منها له استخدامات خاصة. المدى الربيعي (Interquartile Range) يقيس التشتت في النصف الأوسط من البيانات وهو أقل تأثراً بالقيم الشاذة. الانحراف المتوسط المطلق (Mean Absolute Deviation) يستخدم القيم المطلقة بدلاً من التربيع، مما يجعله أسهل في الفهم. الانحراف المعياري المتوسط (Median Absolute Deviation) يعتمد على الوسيط بدلاً من المتوسط ويكون أكثر مقاومة للقيم الشاذة. معامل الاختلاف (Coefficient of Variation) يُستخدم لمقارنة التشتت بين مجموعات بيانات ذات وحدات قياس أو متوسطات مختلفة. اختيار المقياس المناسب يعتمد على طبيعة البيانات والهدف من التحليل.