المثلث قائم الزاوية: خصائصه، نظرياته، وتطبيقاته الشاملة

يشكل المثلث قائم الزاوية حجر أساس في الهندسة الإقليدية، وبوابة نحو فهم أعمق لعلم المثلثات وتطبيقاته الواسعة. هذا الشكل البسيط، بزاويته القائمة المميزة، يفتح آفاقاً لا حصر لها في مختلف فروع العلوم والهندسة.

المقدمة

يُعد المثلث قائم الزاوية (Right-Angled Triangle) أحد أبرز الأشكال الهندسية وأكثرها دراسةً على مر العصور، ليس فقط لبساطة تكوينه ولكن لعمق العلاقات الرياضية التي يحكمها. يتألف هذا الشكل من ثلاثة أضلاع وثلاث زوايا، حيث تكون إحدى زواياه قائمة تماماً، أي ما يعادل 90 درجة، وهي السمة الجوهرية التي تميزه عن سائر أنواع المثلثات. إن وجود هذه الزاوية القائمة يفرض مجموعة فريدة من الخصائص والقوانين التي لا تنطبق إلا على المثلث قائم الزاوية، مما يجعله أداة رياضية قوية بشكل استثنائي. من نظرية فيثاغورس الخالدة، التي تربط بين أطوال أضلاعه، إلى تأسيسه لمجال علم المثلثات بأكمله، لعب المثلث قائم الزاوية دوراً محورياً في تطور الفكر الرياضي. تمتد أهميته إلى ما هو أبعد من الفصول الدراسية والنصوص الأكاديمية، لتتجسد في تطبيقات عملية لا حصر لها تشمل مجالات متنوعة كالهندسة المعمارية، والملاحة، والفيزياء، وحتى الرسومات الحاسوبية، مما يؤكد على أن فهم بنية وخصائص المثلث قائم الزاوية ليس مجرد تمرين أكاديمي، بل هو ضرورة لفهم العالم المادي من حولنا والتفاعل معه بفعالية.

التعريف والخصائص الأساسية للمثلث قائم الزاوية

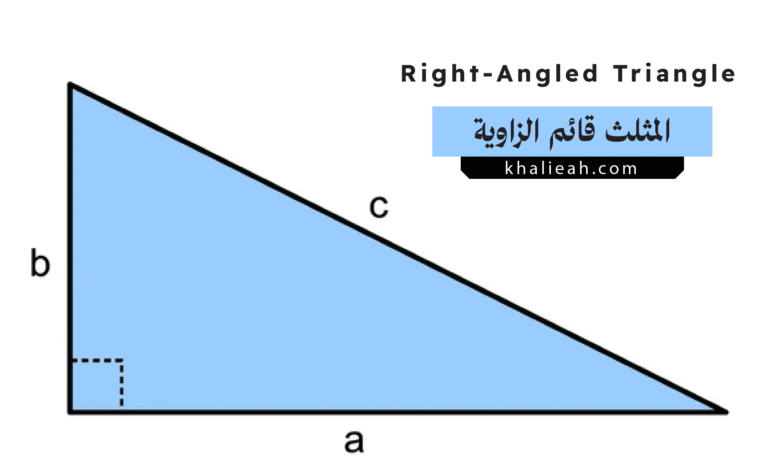
في صميم الهندسة الإقليدية، يُعرَّف المثلث قائم الزاوية بأنه مضلع ثلاثي يحتوي على زاوية واحدة قياسها 90 درجة بالضبط. هذه الزاوية، التي تسمى الزاوية القائمة، هي الخاصية المحددة التي تمنح هذا المثلث اسمه وتفصله عن المثلثات حادة الزوايا (التي جميع زواياها أقل من 90 درجة) والمثلثات منفرجة الزاوية (التي تحتوي على زاوية أكبر من 90 درجة). إن وجود هذه الزاوية يفرض قيوداً وعلاقات محددة على بقية عناصر المثلث. يُطلق على الضلع المقابل للزاوية القائمة اسم الوتر (Hypotenuse)، وهو دائماً أطول ضلع في أي مثلث قائم الزاوية. أما الضلعان الآخران، اللذان يشكلان ضلعي الزاوية القائمة، فيُطلق عليهما اسم الساقين أو الضلعين القائمين (Legs or Cathetus). هذه المصطلحات أساسية لوصف وفهم أي قانون أو نظرية تتعلق بالمثلث قائم الزاوية.

من الخصائص الجوهرية الأخرى للمثلث قائم الزاوية هي العلاقة بين زواياه الحادة. بما أن المجموع الكلي لزوايا أي مثلث في الهندسة المستوية هو 180 درجة، وبما أن إحدى زوايا المثلث قائم الزاوية هي 90 درجة، فإن مجموع الزاويتين الحادتين المتبقيتين يجب أن يكون 90 درجة أيضاً (180 – 90 = 90). تُعرف الزاويتان اللتان مجموعهما 90 درجة بالزاويتين المتتامتين (Complementary Angles). هذه الخاصية مفيدة للغاية في حل المسائل الهندسية، حيث إن معرفة قياس إحدى الزاويتين الحادتين في المثلث قائم الزاوية تكفي تلقائياً لتحديد قياس الزاوية الأخرى. إن هذه البنية المتينة والثابتة هي ما تجعل من المثلث قائم الزاوية أداة تحليلية قوية يمكن الاعتماد عليها في استنتاجات رياضية ومنطقية دقيقة.

نظرية فيثاغورس: حجر الزاوية في دراسة المثلث قائم الزاوية

تُعتبر نظرية فيثاغورس (Pythagorean Theorem) العلاقة الرياضية الأكثر شهرة وارتباطاً بالمثلث قائم الزاوية، وهي تشكل أساساً للعديد من المفاهيم في الهندسة وعلم المثلثات. تنص النظرية على أنه في أي مثلث قائم الزاوية، يكون مربع طول الوتر (الضلع المقابل للزاوية القائمة) مساوياً لمجموع مربعي طولي الضلعين الآخرين (الساقين). إذا رمزنا لطولي الساقين بـ ‘a’ و ‘b’ وطول الوتر بـ ‘c’، فإن العلاقة يمكن التعبير عنها بالصيغة الجبرية الشهيرة: a² + b² = c². هذه المعادلة الأنيقة والبسيطة تخفي وراءها قوة هائلة، فهي تتيح حساب طول أي ضلع في المثلث قائم الزاوية إذا كان طولا الضلعين الآخرين معلومين، مما يجعلها أداة لا غنى عنها في القياسات غير المباشرة.

على الرغم من أن النظرية تُنسب تاريخياً إلى عالم الرياضيات اليوناني فيثاغورس، إلا أن هناك أدلة تشير إلى أن الحضارات القديمة مثل البابليين والمصريين كانت على دراية بهذه العلاقة واستخدمتها في تطبيقات عملية قبل عصر فيثاغورس بقرون. ومع ذلك، يُعتقد أن فيثاغورس أو تلاميذه في مدرسته كانوا أول من قدموا براهين رياضية ومنطقية منظمة لهذه النظرية، مما نقلها من مجرد ملاحظة تجريبية إلى حقيقة رياضية مثبتة. هناك المئات من البراهين المختلفة لنظرية فيثاغورس، بعضها يعتمد على الجبر وبعضها الآخر على الهندسة البصرية، مما يدل على عمق وأهمية هذه العلاقة داخل بنية المثلث قائم الزاوية. إنها ليست مجرد صيغة، بل هي تعبير جوهري عن طبيعة الفضاء الإقليدي ثنائي الأبعاد وكيفية ارتباط الأطوال والمسافات فيه ضمن إطار المثلث قائم الزاوية.

الدوال المثلثية وعلاقتها بالمثلث قائم الزاوية

يمثل المثلث قائم الزاوية مهد علم المثلثات (Trigonometry)، وهو فرع من الرياضيات يدرس العلاقات بين زوايا المثلثات وأطوال أضلاعها. يتم تعريف الدوال المثلثية الأساسية—الجيب (Sine)، وجيب التمام (Cosine)، والظل (Tangent)—بشكل أساسي من خلال نسب أطوال أضلاع المثلث قائم الزاوية. عند النظر إلى إحدى الزاويتين الحادتين في المثلث، ولنطلق عليها اسم (θ)، يمكننا تعريف الأضلاع الثلاثة بالنسبة لهذه الزاوية: الضلع “المقابل” (Opposite) لها، والضلع “المجاور” (Adjacent) لها (وهو ليس الوتر)، و”الوتر” (Hypotenuse). بناءً على هذه التسميات، يتم تعريف الدوال المثلثية الأساسية لأي زاوية حادة θ داخل المثلث قائم الزاوية على النحو التالي:

• دالة الجيب (Sine of θ or sin θ): هي النسبة بين طول الضلع المقابل للزاوية وطول الوتر.
  • الصيغة: sin(θ) = المقابل / الوتر
• دالة جيب التمام (Cosine of θ or cos θ): هي النسبة بين طول الضلع المجاور للزاوية وطول الوتر.
  • الصيغة: cos(θ) = المجاور / الوتر
• دالة الظل (Tangent of θ or tan θ): هي النسبة بين طول الضلع المقابل للزاوية وطول الضلع المجاور لها.
  • الصيغة: tan(θ) = المقابل / المجاور

هذه النسب تظل ثابتة لزاوية معينة بغض النظر عن حجم المثلث قائم الزاوية، طالما أنه يحتوي على تلك الزاوية. هذه الخاصية، المعروفة باسم خاصية التشابه، هي التي تجعل علم المثلثات أداة قوية. بالإضافة إلى هذه الدوال الأساسية، هناك ثلاث دوال أخرى هي مقلوباتها: قاطع التمام (Cosecant)، والقاطع (Secant)، وظل التمام (Cotangent). تسمح هذه الدوال بحل أي مثلث قائم الزاوية، أي إيجاد جميع أطوال أضلاعه وقياسات زواياه إذا توفرت معلومات كافية (مثل طول ضلعين، أو طول ضلع وقياس زاوية). إن القدرة على الربط بين الزوايا والأضلاع بهذه الطريقة الدقيقة هي ما يجعل المثلث قائم الزاوية أساسياً في مجالات مثل الفيزياء، والملاحة، والهندسة.

أنواع خاصة من المثلث قائم الزاوية

ضمن فئة المثلث قائم الزاوية، هناك أنواع خاصة تظهر بشكل متكرر في المسائل الرياضية والتطبيقات العملية، وتتميز بنسب ثابتة بين أطوال أضلاعها، مما يسهل الحسابات بشكل كبير. هذه المثلثات الخاصة هي أدوات مختصرة قوية تختصر الحاجة إلى تطبيق نظرية فيثاغورس أو الدوال المثلثية في كل مرة. أبرز هذه الأنواع هما المثلث القائم المتساوي الساقين والمثلث 30-60-90. إن دراسة هذه الحالات الخاصة من المثلث قائم الزاوية توفر فهماً أعمق للعلاقات الهندسية.

يمتلك كل نوع من هذين النوعين خصائص فريدة تجعله مميزاً. إن حفظ نسب أضلاعهما يساعد بشكل كبير في حل المسائل بسرعة وكفاءة، وهي تمثل حالات مثالية تُبنى عليها العديد من البراهين الهندسية والمشكلات التطبيقية. فيما يلي تفصيل لكل نوع:

• المثلث قائم الزاوية المتساوي الساقين (Isosceles Right-Angled Triangle):
  • الزوايا: يُعرف هذا المثلث أيضاً باسم مثلث 45-45-90. بما أنه مثلث قائم الزاوية، فإحدى زواياه 90 درجة. ولكونه متساوي الساقين، يجب أن تكون الزاويتان الأخريان متساويتين. وبما أن مجموعهما يجب أن يكون 90 درجة، فإن قياس كل منهما هو 45 درجة.
  • الأضلاع: لأن زاويتي القاعدة متساويتان، فإن الضلعين المقابلين لهما (الساقين) يكونان متساويين في الطول. إذا افترضنا أن طول كل ساق هو ‘x’، فيمكننا استخدام نظرية فيثاغورس لإيجاد طول الوتر: x² + x² = c²، مما يؤدي إلى 2x² = c²، وبالتالي فإن c = x√2.
  • نسبة الأضلاع: تكون نسبة أطوال الأضلاع في هذا النوع من المثلث قائم الزاوية دائماً x : x : x√2.
• مثلث 30-60-90 (The 30-60-90 Triangle):
  • الزوايا: كما يوحي اسمه، زوايا هذا المثلث هي 30 درجة، و60 درجة، و90 درجة. يمكن اعتباره نصف مثلث متساوي الأضلاع تم قطعه من أحد رؤوسه إلى منتصف الضلع المقابل.
  • الأضلاع: العلاقة بين أضلاع هذا المثلث ثابتة ومميزة. الضلع الأقصر هو دائماً المقابل للزاوية 30 درجة. الوتر يكون دائماً ضعف طول الضلع الأقصر. والضلع المتبقي (المقابل للزاوية 60 درجة) يكون طوله مساوياً لطول الضلع الأقصر مضروباً في √3.
  • نسبة الأضلاع: إذا كان طول الضلع المقابل للزاوية 30 درجة هو ‘x’، فإن طول الوتر سيكون ‘2x’، وطول الضلع المقابل للزاوية 60 درجة سيكون ‘x√3’. بالتالي، تكون نسبة الأضلاع دائماً x : x√3 : 2x.

حساب المساحة والمحيط للمثلث قائم الزاوية

يُعد حساب المساحة والمحيط من القياسات الأساسية لأي شكل هندسي، وفي حالة المثلث قائم الزاوية، تتميز هذه الحسابات ببساطة ووضوح استثنائيين بفضل وجود الزاوية القائمة. فبالنسبة للمحيط (Perimeter)، وهو الطول الإجمالي للحد الخارجي للشكل، فإن حسابه لا يختلف عن أي مثلث آخر. يتم الحصول عليه ببساطة عن طريق جمع أطوال الأضلاع الثلاثة. إذا كانت أطوال الساقين هي ‘a’ و ‘b’ وطول الوتر هو ‘c’، فإن محيط المثلث قائم الزاوية يُعطى بالصيغة: المحيط = a + b + c. على الرغم من بساطة الصيغة، فإن تحديد المحيط غالباً ما يتطلب خطوة إضافية تتمثل في استخدام نظرية فيثاغورس لإيجاد طول الضلع المجهول قبل التمكن من جمع الأطوال الثلاثة.

أما بالنسبة لحساب المساحة (Area)، فإن طبيعة المثلث قائم الزاوية تقدم ميزة فريدة. الصيغة العامة لمساحة أي مثلث هي نصف حاصل ضرب طول القاعدة في طول الارتفاع العمودي عليها (Area = ½ * base * height). في المثلثات الأخرى، قد يتطلب إيجاد الارتفاع إنشاء خط عمودي إضافي. لكن في المثلث قائم الزاوية، يكون أحد الساقين عمودياً بالفعل على الساق الآخر. هذا يعني أنه يمكننا اعتبار أحد الساقين “قاعدة” والآخر “ارتفاعاً” بشكل مباشر. لذلك، تصبح صيغة حساب مساحة المثلث قائم الزاوية بسيطة جداً: المساحة = ½ * a * b، حيث ‘a’ و ‘b’ هما طولا الساقين. هذه السهولة في حساب المساحة تجعل المثلث قائم الزاوية مكوناً أساسياً في طرق حساب المساحات الأكثر تعقيداً، مثل طريقة التكامل في حساب التفاضل والتكامل، حيث يتم تقريب مساحة الأشكال المنحنية باستخدام سلسلة من المستطيلات أو المثلثات القائمة الصغيرة.

الدائرة المحيطة والدائرة الداخلية للمثلث قائم الزاوية

يمتلك المثلث قائم الزاوية علاقات هندسية مثيرة للاهتمام مع الدوائر، وتحديداً الدائرة المحيطة به (Circumcircle) والدائرة الداخلية (Incircle). الدائرة المحيطة هي الدائرة التي تمر بجميع رؤوس المثلث الثلاثة. بالنسبة لأي مثلث قائم الزاوية، هناك خاصية فريدة وأنيقة: يكون الوتر هو قطر الدائرة المحيطة به. هذا يعني أن مركز الدائرة المحيطة (Circumcenter) يقع تماماً عند نقطة منتصف الوتر. هذه الحقيقة، المعروفة بنظرية تاليس (Thales’ Theorem)، تنص على أنه إذا كانت النقاط A و B و C هي رؤوس مثلث، وكانت الزاوية عند C قائمة، فإن هذه النقاط تقع على دائرة قطرها هو القطعة المستقيمة AB (الوتر). هذه الخاصية تسهل بشكل كبير تحديد مركز ونصف قطر الدائرة المحيطة لأي مثلث قائم الزاوية، حيث إن نصف القطر (Circumradius) يساوي ببساطة نصف طول الوتر.

على الجانب الآخر، الدائرة الداخلية هي أكبر دائرة يمكن رسمها داخل المثلث بحيث تمس جميع أضلاعه الثلاثة. مركز هذه الدائرة (Incenter) هو نقطة تقاطع منصفات زوايا المثلث، ونصف قطرها (Inradius) هو المسافة العمودية من المركز إلى أي من الأضلاع. في حالة المثلث قائم الزاوية، يمكن حساب نصف قطر الدائرة الداخلية ‘r’ باستخدام صيغة بسيطة ترتبط بأطوال أضلاعه. إذا كانت أطوال الساقين هي ‘a’ و ‘b’ وطول الوتر هو ‘c’، فإن نصف قطر الدائرة الداخلية يُعطى بالعلاقة: r = (a + b – c) / 2. هذه الصيغة تربط بين الهندسة الخطية للمثلث (أضلاعه) والهندسة الدائرية المرتبطة به. إن فهم هذه العلاقات بين المثلث قائم الزاوية والدوائر المحيطة والداخلية يوفر رؤى أعمق حول التناظر والخصائص الهيكلية الكامنة في هذا الشكل الهندسي الأساسي.

تطبيقات المثلث قائم الزاوية في العلوم والهندسة

تتجاوز أهمية المثلث قائم الزاوية حدود الرياضيات النظرية لتصبح أداة عملية لا غنى عنها في مجموعة واسعة من التخصصات العلمية والهندسية. أحد أبرز التطبيقات يكمن في مجال المسح والملاحة. يستخدم المساحون مبادئ علم المثلثات، التي تعتمد بشكل أساسي على المثلث قائم الزاوية، لقياس المسافات والارتفاعات التي يصعب الوصول إليها بشكل مباشر. من خلال قياس زاوية الارتفاع (Angle of Elevation) من نقطة على الأرض إلى قمة مبنى أو جبل، ومعرفة المسافة الأفقية إلى قاعدة ذلك الجسم، يمكنهم تكوين مثلث قائم الزاوية وحساب ارتفاعه بدقة. وبالمثل، تستخدم تقنيات التثليث (Triangulation) في أنظمة تحديد المواقع العالمية (GPS) وفي رسم الخرائط لتحديد المواقع بدقة عبر شبكة من المثلثات.

في مجال الهندسة المعمارية والإنشاءات، يعد ضمان وجود زوايا قائمة دقيقة أمراً حيوياً لسلامة واستقرار الهياكل. يستخدم البناؤون منذ القدم “قاعدة 3-4-5″، وهي تطبيق مباشر لنظرية فيثاغورس، للتأكد من أن الزوايا مربعة تماماً. إذا تم قياس 3 وحدات على طول أحد الجدران و 4 وحدات على طول الجدار الآخر من الركن، فيجب أن تكون المسافة القطرية بين هاتين النقطتين 5 وحدات بالضبط لكي تكون الزاوية 90 درجة. علاوة على ذلك، يعتمد تصميم السلالم، والمنحدرات، وهياكل الأسقف (الجمالونات) بشكل كبير على حسابات المثلث قائم الزاوية لضمان الميل والارتفاع والدعم الهيكلي المناسب. أما في الفيزياء، فإن المثلث قائم الزاوية ضروري لتحليل المتجهات (Vectors). يتم تحليل قوى مثل الجاذبية، أو الاحتكاك، أو السرعة إلى مكوناتها الأفقية والعمودية، مما يشكل ساقي مثلث قائم الزاوية ويكون المتجه الأصلي هو الوتر. هذا التبسيط يسمح للفيزيائيين بتحليل حركة الأجسام على الأسطح المائلة أو مسار المقذوفات بسهولة أكبر، مما يوضح كيف أن المثلث قائم الزاوية هو لغة أساسية لوصف العالم المادي.

المثلث قائم الزاوية في السياقات الرياضية المتقدمة

لا تقتصر فائدة المثلث قائم الزاوية على الهندسة الإقليدية الأساسية، بل تمتد لتلعب دوراً جوهرياً في فروع الرياضيات الأكثر تقدماً. في الهندسة التحليلية أو الديكارتية (Coordinate Geometry)، تُبنى صيغة المسافة بين نقطتين في المستوى مباشرة على نظرية فيثاغورس. المسافة الأفقية (Δx) والمسافة الرأسية (Δy) بين نقطتين تشكلان ساقي مثلث قائم الزاوية، والمسافة المستقيمة بينهما هي الوتر. وبالتالي، فإن صيغة المسافة d = √((Δx)² + (Δy)²) ليست سوى إعادة صياغة لنظرية فيثاغورس في نظام الإحداثيات. كما يستخدم مفهوم المثلث قائم الزاوية لإثبات تعامد خطين مستقيمين، حيث يكونان متعامدين إذا وفقط إذا كان حاصل ضرب ميليهما يساوي -1، وهي خاصية يمكن اشتقاقها من العلاقات المثلثية داخل المثلثات القائمة التي تشكلها هذه الخطوط مع المحاور.

في عالم الأعداد المركبة (Complex Numbers)، يوفر المثلث قائم الزاوية تمثيلاً بصرياً قوياً. عند تمثيل عدد مركب z = a + bi على المستوى المركب (مخطط أرجاند)، فإن الجزء الحقيقي ‘a’ يمثل الإحداثي الأفقي والجزء التخيلي ‘b’ يمثل الإحداثي الرأسي. المسافة من نقطة الأصل إلى النقطة (a, b)، والتي تُعرف بمعيار أو قيمة العدد المركب المطلقة (|z|)، هي وتر المثلث قائم الزاوية الذي تشكل ‘a’ و ‘b’ ساقيه. بالتالي، يتم حساب المعيار باستخدام نظرية فيثاغورس: |z| = √(a² + b²). علاوة على ذلك، في جبر المتجهات (Vector Algebra)، يتم تعميم نظرية فيثاغورس إلى أبعاد أعلى لحساب مقدار (طول) المتجهات. ففي الفضاء ثلاثي الأبعاد، مقدار المتجه v = (x, y, z) هو ||v|| = √(x² + y² + z²). إن مفهوم التعامد (Orthogonality)، وهو تعميم للزاوية القائمة، أساسي في دراسة الفضاءات المتجهية، حيث يعتبر المثلث قائم الزاوية الحالة ثنائية الأبعاد لهذه الفكرة الأوسع.

الخاتمة

في الختام، يتضح أن المثلث قائم الزاوية هو أكثر بكثير من مجرد شكل هندسي بسيط. إنه مفهوم رياضي أساسي ذو عمق هائل، يمتد تأثيره من المبادئ الهندسية الأولى إلى أعقد النظريات في الرياضيات والعلوم. من خلال زاويته القائمة المميزة، يفرض المثلث قائم الزاوية نظاماً ودقة، مما يؤدي إلى علاقات خالدة مثل نظرية فيثاغورس التي شكلت فهمنا للمسافة والفضاء. لقد كان المثلث قائم الزاوية هو اللبنة الأساسية التي بُني عليها صرح علم المثلثات بأكمله، مما منحنا الأدوات اللازمة لربط الزوايا بالأضلاع وقياس العالم من حولنا بطرق لم تكن ممكنة لولاه. إن تطبيقاته العملية، التي تتراوح من تشييد المباني الشاهقة إلى استكشاف الفضاء وتحليل القوى الفيزيائية، تبرهن على أنه ليس مجرد فكرة مجردة، بل أداة حيوية تسهم في تشكيل واقعنا التكنولوجي. إن دراسة المثلث قائم الزاوية تظل رحلة أساسية لأي طالب علم، فهي لا تكشف فقط عن جمال التناظر الرياضي، بل تمنح أيضاً مفتاحاً لفهم العديد من الظواهر الطبيعية والهندسية التي تحكم عالمنا.

أسئلة شائعة

1. ما الذي يميز المثلث قائم الزاوية عن غيره من المثلثات؟
السمة المحددة للمثلث قائم الزاوية هي وجود زاوية واحدة يبلغ قياسها 90 درجة بالضبط، تُعرف بالزاوية القائمة. هذه الخاصية تفرض علاقات فريدة بين أضلاعه وزواياه، مثل نظرية فيثاغورس، والتي لا تنطبق على المثلثات حادة أو منفرجة الزاوية.

2. ما هي نظرية فيثاغورس وما أهميتها؟
نظرية فيثاغورس هي علاقة رياضية أساسية تنص على أنه في أي مثلث قائم الزاوية، فإن مربع طول الوتر (الضلع المقابل للزاوية القائمة) يساوي مجموع مربعي طولي الضلعين الآخرين (الساقين). صيغتها هي a² + b² = c²، وتكمن أهميتها في قدرتها على حساب طول ضلع مجهول بمعرفة الضلعين الآخرين.

3. ما هو الوتر وما هي خصائصه؟
الوتر (Hypotenuse) هو الضلع المقابل للزاوية القائمة في المثلث قائم الزاوية. يتميز بأنه أطول ضلع في المثلث دائماً. وفي سياق الدائرة المحيطة بالمثلث، يمثل الوتر قطر تلك الدائرة.

4. كيف تُعرّف الدوال المثلثية الأساسية باستخدام المثلث قائم الزاوية؟
تُعرّف الدوال المثلثية الرئيسية (الجيب، جيب التمام، الظل) كنسب بين أطوال أضلاع المثلث قائم الزاوية بالنسبة لإحدى زواياه الحادة (θ):

• الجيب (sin θ) = الضلع المقابل / الوتر.
• جيب التمام (cos θ) = الضلع المجاور / الوتر.
• الظل (tan θ) = الضلع المقابل / الضلع المجاور.

5. ما هي العلاقة بين الزاويتين الحادتين في المثلث قائم الزاوية؟
بما أن مجموع زوايا أي مثلث هو 180 درجة وإحدى الزوايا هي 90 درجة، فإن مجموع الزاويتين الحادتين المتبقيتين يجب أن يكون 90 درجة. لذلك، فهما زاويتان متتامتان (Complementary Angles).

6. هل يمكن أن يكون المثلث قائم الزاوية متساوي الساقين؟
نعم، يُعرف هذا النوع بالمثلث القائم المتساوي الساقين أو مثلث 45-45-90. في هذه الحالة، يكون الضلعان المكونان للزاوية القائمة (الساقان) متساويين في الطول، وتكون الزاويتان الحادتان متساويتين، قياس كل منهما 45 درجة.

7. كيف يتم حساب مساحة المثلث قائم الزاوية؟
يتم حساب مساحته ببساطة عن طريق ضرب طولي الضلعين القائمين (الساقين) ثم قسمة الناتج على اثنين. الصيغة هي: المساحة = ½ × (طول الساق الأول) × (طول الساق الثاني)، حيث يعمل أحد الساقين كقاعدة والآخر كارتفاع.

8. ما هي “ثلاثية فيثاغورس” وما أشهر مثال عليها؟
ثلاثية فيثاغورس هي مجموعة من ثلاثة أعداد صحيحة موجبة (a, b, c) تحقق المعادلة a² + b² = c². يمكن لهذه الأعداد أن تمثل أطوال أضلاع مثلث قائم الزاوية. أشهر مثال هو الثلاثية (3, 4, 5)، حيث 3² + 4² = 9 + 16 = 25 = 5².

9. أين يقع مركز الدائرة التي تمر برؤوس المثلث قائم الزاوية؟
مركز الدائرة المحيطة بالمثلث قائم الزاوية (Circumcenter) يقع دائماً في نقطة منتصف الوتر. هذه الخاصية تجعل من السهل جداً تحديد مركز ونصف قطر هذه الدائرة.

10. كيف يُستخدم المثلث قائم الزاوية في تحليل المتجهات؟
في الفيزياء والهندسة، يتم تحليل المتجهات (مثل القوة أو السرعة) إلى مكوناتها المتعامدة (الأفقية والرأسية). هذه المكونات تشكل ساقي مثلث قائم الزاوية، ويكون المتجه الأصلي هو الوتر. هذا التبسيط يسهل الحسابات وتحليل الأنظمة المعقدة.

---

اختبار قصير (Quiz)

اختر الإجابة الأنسب لكل سؤال مما يلي:

1. ما هو مجموع قياس الزاويتين الحادتين في أي مثلث قائم الزاوية؟
   أ) 180 درجة
   ب) 90 درجة
   ج) 45 درجة
2. أي من المعادلات التالية تمثل نظرية فيثاغورس حيث c هو الوتر؟
   أ) a² + c² = b²
   ب) a + b = c
   ج) a² + b² = c²
3. الضلع المقابل للزاوية 90 درجة في المثلث قائم الزاوية يسمى:
   أ) الساق
   ب) الوتر
   ج) الارتفاع
4. في المثلث قائم الزاوية، نسبة الضلع المقابل إلى الوتر تعرف بـ:
   أ) جيب الزاوية (Sine)
   ب) ظل الزاوية (Tangent)
   ج) جيب تمام الزاوية (Cosine)
5. ما هي قياسات زوايا المثلث قائم الزاوية المتساوي الساقين؟
   أ) 30-60-90
   ب) 45-45-90
   ج) 60-60-60
6. إذا كان طولا الساقين في مثلث قائم الزاوية هما 6 سم و 8 سم، فما هي مساحته؟
   أ) 48 سم²
   ب) 24 سم²
   ج) 14 سم²
7. في مثلث 30-60-90، يكون طول الوتر دائماً:
   أ) ضعف طول الضلع الأقصر
   ب) مساوياً لطول الضلع الأطول
   ج) نصف طول الضلع الأقصر
8. أين يقع مركز الدائرة المحيطة بالمثلث قائم الزاوية؟
   أ) عند الرأس القائم
   ب) داخل المثلث
   ج) في منتصف الوتر
9. نسبة الضلع المقابل إلى الضلع المجاور لزاوية حادة تعرف بـ:
   أ) القاطع (Secant)
   ب) جيب التمام (Cosine)
   ج) الظل (Tangent)
10. إذا كان طول أحد الساقين في مثلث قائم الزاوية 5 وطول الوتر 13، فما طول الساق الآخر؟
    أ) 8
    ب) 12
    ج) 18

الإجابات الصحيحة:

1. ب
2. ج
3. ب
4. أ
5. ب
6. ب
7. أ
8. ج
9. ج
10. ب