تشفير المنحنى الإهليلجي: الثورة الهادئة في عالم أمن المعلومات الحديث

مقدمة في عالم التشفير غير المتماثل

في العصر الرقمي الذي نعيشه، أصبح أمن المعلومات حجر الزاوية في كل تفاعل إلكتروني، بدءاً من المعاملات المصرفية عبر الإنترنت وانتهاءً بالرسائل الفورية المشفرة. يعتمد هذا الأمن بشكل كبير على مجال علمي يُعرف بالتشفير (Cryptography)، والذي ينقسم إلى فرعين رئيسيين: التشفير المتماثل والتشفير غير المتماثل (أو تشفير المفتاح العام). بينما يستخدم التشفير المتماثل مفتاحاً واحداً للتشفير وفك التشفير، يعتمد التشفير غير المتماثل على زوج من المفاتيح: مفتاح عام متاح للجميع لتشفير البيانات، ومفتاح خاص يحتفظ به المالك سراً لفك التشفير. هذا النموذج الأخير أحدث ثورة في الاتصالات الآمنة، حيث سمح بتبادل المفاتيح والتوقيعات الرقمية دون الحاجة إلى قناة آمنة مسبقاً. لسنوات طويلة، هيمنت خوارزمية RSA على هذا المجال، ولكن مع تزايد القدرات الحاسوبية، ظهرت الحاجة إلى بديل أكثر كفاءة وقوة. من هنا، بزغ نجم تشفير المنحنى الإهليلجي (Elliptic Curve Cryptography – ECC) كحل متفوق يقدم نفس مستوى الأمان بمفاتيح أقصر بكثير، مما يجعله العمود الفقري للعديد من التطبيقات الأمنية الحديثة. إن فهم آلية عمل تشفير المنحنى الإهليلجي يتطلب الغوص في أسسه الرياضية العميقة، والتي تجمع بين جماليات الهندسة وقوة نظرية المجموعات.

الأسس الرياضية لتشفير المنحنى الإهليلجي

يكمن جوهر قوة تشفير المنحنى الإهليلجي في الرياضيات المعقدة التي يقوم عليها. على عكس RSA، التي تعتمد على صعوبة تحليل الأعداد الكبيرة إلى عواملها الأولية، يستمد تشفير المنحنى الإهليلجي أمانه من صعوبة “مسألة اللوغاريتم المتقطع للمنحنى الإهليلجي” (Elliptic Curve Discrete Logarithm Problem – ECDLP). لفهم ذلك، يجب أولاً تعريف المنحنى الإهليلجي نفسه.

المنحنى الإهليلجي ليس شكلاً إهليلجياً (بيضوياً) كما قد يوحي اسمه، بل هو مجموعة من النقاط التي تحقق معادلة جبرية محددة. في أبسط صورها على حقل من الأعداد الحقيقية، تُعرف معادلة المنحنى الإهليلجي (في شكل Weierstrass) بالصيغة التالية:

y^2 = x^3 + ax + b

حيث يجب أن يحقق المعاملان a و b شرطاً معيناً لضمان عدم وجود نقاط شاذة (singular points) على المنحنى، وهو 4a^3 + 27b^2 ≠ 0. هذا الشرط يضمن أن للمنحنى مماساً فريداً عند كل نقطة. إن مجموعة النقاط (x, y) التي تحقق هذه المعادلة، بالإضافة إلى نقطة خاصة تسمى “النقطة في اللانهاية” (Point at Infinity)، والتي يُرمز لها بـ O، تشكل بنية رياضية فريدة تُعرف بـ “المجموعة الأبيلية” (Abelian Group). هذه الخاصية هي التي تجعل تشفير المنحنى الإهليلجي ممكناً.

خصائص المجموعة الأبيلية تعني أن هناك عملية “جمع” معرفة على نقاط المنحنى، وهذه العملية تحقق الشروط التالية:

1. الانغلاق (Closure): جمع أي نقطتين على المنحنى ينتج عنه نقطة ثالثة تقع على نفس المنحنى.
2. التجميع (Associativity): (P + Q) + R = P + (Q + R) لأي نقاط P, Q, R على المنحنى.
3. العنصر المحايد (Identity Element): توجد نقطة محايدة (النقطة في اللانهاية O) بحيث أن P + O = P لأي نقطة P.
4. العنصر المعكوس (Inverse Element): لكل نقطة P على المنحنى، يوجد معكوس (-P) بحيث أن P + (-P) = O.

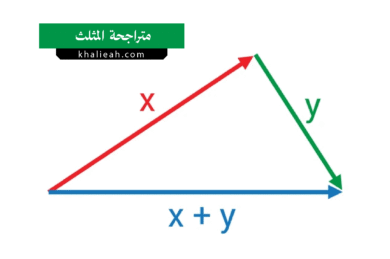
عملية الجمع هذه ليست جمعاً جبرياً تقليدياً، بل هي عملية هندسية تُعرف بقاعدة “الوتر والمماس” (Chord-and-Tangent Rule). لجمع نقطتين مختلفتين P و Q، نرسم خطاً مستقيماً يمر عبرهما. سيقطع هذا الخط المنحنى عند نقطة ثالثة (دعنا نسميها -R). إن ناتج جمع P + Q هو انعكاس النقطة -R حول المحور السيني، أي النقطة R. أما لجمع نقطة مع نفسها (P + P أو 2P)، نرسم المماس للمنحنى عند النقطة P. سيقطع هذا المماس المنحنى عند نقطة أخرى (-R)، ويكون الناتج هو انعكاسها R. هذه العمليات الحسابية هي التي تشكل أساس كل بروتوكولات تشفير المنحنى الإهليلجي.

الانتقال إلى الحقول المنتهية: مفتاح التطبيق العملي

إن العمل على المنحنيات الإهليلجية في حقل الأعداد الحقيقية مفيد للشرح النظري، ولكنه غير عملي للتشفير بسبب مشاكل الدقة والحجم اللانهائي. لذا، يتم تطبيق تشفير المنحنى الإهليلجي على “حقول منتهية” (Finite Fields)، وتحديداً نوعين:

1. الحقول الأولية (Prime Fields F_p): حيث تكون جميع العمليات الحسابية (الجمع والضرب) مقيدة بالباقي من القسمة على عدد أولي كبير p. المعادلة تصبح:
   y^2 ≡ x^3 + ax + b (mod p)
   هنا، الإحداثيات x و y هي أعداد صحيحة بين 0 و p-1.
2. الحقول الثنائية (Binary Fields F_2^m): تستخدم في تطبيقات العتاد (Hardware) لأن العمليات الحسابية فيها (باستخدام كثيرات الحدود) يمكن تنفيذها بكفاءة عالية على مستوى البتات.

إن الانتقال إلى الحقول المنتهية يحول المنحنى المستمر إلى مجموعة متقطعة من النقاط، مما يجعله مثالياً للتطبيقات الحاسوبية. في هذا السياق، يصبح مفهوم “الضرب القياسي” (Scalar Multiplication) هو العملية المحورية في تشفير المنحنى الإهليلجي. الضرب القياسي هو تكرار لعملية الجمع:

Q = k * P = P + P + ... + P (k مرة)

هنا، P هي نقطة على المنحنى (تُعرف بالنقطة الأساسية أو الموّلد G)، و k هو عدد صحيح. من السهل جداً حساب النقطة Q إذا كانت k و P معروفتين. ولكن، من الصعب جداً من الناحية الحسابية (مستحيل عملياً للأعداد الكبيرة المستخدمة في التشفير) إيجاد العدد k إذا كانت النقطتان Q و P معروفتين. هذه هي “مسألة اللوغاريتم المتقطع للمنحنى الإهليلجي” (ECDLP)، وهي المشكلة الصعبة التي يستند إليها كامل أمان تشفير المنحنى الإهليلجي. إن k يمثل المفتاح الخاص، بينما Q تمثل المفتاح العام.

آلية عمل تشفير المنحنى الإهليلجي في التطبيقات

بعد فهم الأسس الرياضية، يمكننا الآن استكشاف كيفية استخدام تشفير المنحنى الإهليلجي في بروتوكولات العالم الحقيقي، مثل تبادل المفاتيح والتوقيعات الرقمية.

إنشاء المفاتيح (Key Generation)

قبل أي عملية، يجب أن يتفق الطرفان على معلمات النطاق (Domain Parameters) الخاصة بالمنحنى، والتي تشمل:

• المعاملان a و b من معادلة المنحنى.
• العدد الأولي p (في حالة الحقل الأولي).
• النقطة الأساسية G (Base Point) على المنحنى.
• رتبة G، وهي أصغر عدد صحيح n بحيث n * G = O.

لإنشاء زوج من المفاتيح، يقوم المستخدم (لنسميه أليس) بالخطوات التالية:

1. تختار أليس عدداً صحيحاً عشوائياً d_A (المفتاح الخاص) من المجال [1, n-1].
2. تحسب أليس المفتاح العام Q_A عن طريق عملية الضرب القياسي: Q_A = d_A * G.

المفتاح الخاص d_A يجب أن يبقى سرياً تماماً، بينما المفتاح العام Q_A (وهو نقطة على المنحنى) يمكن نشره للجميع. إن قوة تشفير المنحنى الإهليلجي تكمن في أنه حتى لو عرف المهاجم Q_A و G، فإنه لا يستطيع حساب d_A.

تبادل المفاتيح باستخدام (Elliptic Curve Diffie-Hellman – ECDH)

بروتوكول ECDH هو تطبيق مباشر لـ تشفير المنحنى الإهليلجي لإنشاء سر مشترك بين طرفين (أليس وبوب) عبر قناة غير آمنة.

1. أليس وبوب يتفقان مسبقاً على معلمات النطاق للمنحنى (بما في ذلك النقطة G).
2. أليس تنشئ زوج مفاتيحها: مفتاح خاص d_A ومفتاح عام Q_A = d_A * G.
3. بوب ينشئ زوج مفاتيحه: مفتاح خاص d_B ومفتاح عام Q_B = d_B * G.
4. أليس ترسل مفتاحها العام Q_A إلى بوب، وبوب يرسل مفتاحه العام Q_B إلى أليس.
5. أليس تستخدم مفتاحها الخاص d_A ومفتاح بوب العام Q_B لحساب السر المشترك:
   S = d_A * Q_B = d_A * (d_B * G) = (d_A * d_B) * G
6. بوب يستخدم مفتاحه الخاص d_B ومفتاح أليس العام Q_A لحساب السر المشترك:
   S = d_B * Q_A = d_B * (d_A * G) = (d_B * d_A) * G

بفضل خاصية التجميع، يصل كل من أليس وبوب إلى نفس النقطة S على المنحنى، والتي تمثل سراً مشتركاً. يمكنهما بعد ذلك استخدام إحداثيات هذه النقطة كمفتاح لتشفير متماثل (مثل AES). أي متصنت على القناة سيعرف G, Q_A, Q_B، ولكنه لن يتمكن من حساب السر المشترك S لأنه لا يعرف d_A أو d_B. هذه الكفاءة تجعل من تشفير المنحنى الإهليلجي مثالياً لبروتوكولات مثل TLS المستخدم في تأمين مواقع الويب (HTTPS).

التوقيعات الرقمية باستخدام (Elliptic Curve Digital Signature Algorithm – ECDSA)

ECDSA هو تطبيق آخر حيوي لـ تشفير المنحنى الإهليلجي، يُستخدم للتحقق من هوية المرسل وسلامة البيانات. هذا هو النظام المستخدم في العملات المشفرة مثل بيتكوين وإيثريوم.

عملية التوقيع (بواسطة أليس):

1. تقوم أليس بحساب “هاش” (Hash) للرسالة M باستخدام دالة هاش آمنة (مثل SHA-256)، لنحصل على h.
2. تختار أليس عدداً عشوائياً مؤقتاً k.
3. تحسب النقطة R = k * G. الإحداثي السيني لهذه النقطة r = R_x.
4. تحسب قيمة التوقيع s باستخدام المعادلة: s = k⁻¹ * (h + r * d_A) mod n.
5. التوقيع الرقمي هو الزوج (r, s). ترسله أليس مع الرسالة M.

عملية التحقق (بواسطة بوب):

1. يتلقى بوب الرسالة M والتوقيع (r, s).
2. يحسب بوب هاش الرسالة h بنفس الدالة التي استخدمتها أليس.
3. يحسب القيمتين التاليتين:
   u1 = h * s⁻¹ mod n
u2 = r * s⁻¹ mod n
4. يحسب النقطة P = u1 * G + u2 * Q_A.
5. إذا كان الإحداثي السيني للنقطة P (أي P_x) يساوي r، فإن التوقيع صحيح.

إن صحة هذا التحقق تنبع من علاقات رياضية معقدة ضمن بنية تشفير المنحنى الإهليلجي. إذا تم تعديل الرسالة أو التوقيع، أو إذا حاول شخص آخر التوقيع باستخدام مفتاح أليس العام، فإن عملية التحقق ستفشل حتماً. هذا يعطينا خاصيتي الأصالة (Authentication) وعدم الإنكار (Non-repudiation)، وهما أساسيتان في المعاملات الرقمية الآمنة. إن كفاءة تشفير المنحنى الإهليلجي في هذا المجال واضحة جداً.

مقارنة بين تشفير المنحنى الإهليلجي و RSA

لفهم سبب هيمنة تشفير المنحنى الإهليلجي اليوم، من الضروري مقارنته بسلفه، خوارزمية RSA.

مستوى الأمان (بت)	طول مفتاح ECC (بت)	طول مفتاح RSA (بت)	نسبة طول المفتاح (RSA/ECC)
80	160	1024	6.4 : 1
112	224	2048	9.1 : 1
128	256	3072	12 : 1
192	384	7680	20 : 1
256	512	15360	30 : 1

الجدول أعلاه يوضح الميزة الأبرز لـ تشفير المنحنى الإهليلجي: حجم المفتاح. لتحقيق مستوى أمان 128 بت (وهو معيار شائع اليوم)، يتطلب تشفير المنحنى الإهليلجي مفتاحاً بطول 256 بت فقط، بينما تحتاج RSA إلى مفتاح بطول 3072 بت. هذه الفجوة تتسع بشكل كبير مع زيادة مستوى الأمان المطلوب.

هذه الميزة لها آثار عملية هائلة:

• كفاءة في التخزين: المفاتيح الأقصر تتطلب مساحة تخزين أقل، وهو أمر حيوي في الأجهزة ذات الموارد المحدودة مثل بطاقات الائتمان الذكية وأجهزة إنترنت الأشياء (IoT).
• كفاءة في النقل: الشهادات الرقمية والتوقيعات التي يستخدمها تشفير المنحنى الإهليلجي أصغر حجماً، مما يقلل من استهلاك عرض النطاق الترددي ويسرّع من عمليات المصافحة (Handshake) في بروتوكولات مثل TLS.
• كفاءة في الحوسبة: على الرغم من أن العمليات الرياضية في تشفير المنحنى الإهليلجي أكثر تعقيداً من RSA، إلا أن حجم الأعداد الأصغر بكثير يجعل العمليات الحاسوبية (خاصة إنشاء التوقيع وتبادل المفاتيح) أسرع بشكل عام، مما يقلل من الحمل على الخوادم ويوفر الطاقة في الأجهزة المحمولة.

لهذه الأسباب، أصبح تشفير المنحنى الإهليلجي الخيار المفضل في معظم التطبيقات الحديثة التي تتطلب أداءً عالياً وأماناً قوياً.

تحديات وأمن تشفير المنحنى الإهليلجي

على الرغم من قوته، لا يخلو تشفير المنحنى الإهليلجي من التحديات والمخاطر التي يجب التعامل معها بحذر.

1. اختيار المنحنى: ليس كل منحنى إهليلجي آمناً. يجب اختيار منحنيات ذات معلمات تم فحصها بدقة من قبل خبراء التشفير. المنحنيات التي تحتوي على نقاط ضعف رياضية يمكن أن تسهل حل مسألة اللوغاريتم المتقطع. لهذا السبب، توصي المنظمات القياسية مثل المعهد الوطني للمعايير والتكنولوجيا (NIST) باستخدام مجموعة محددة من المنحنيات (مثل P-256, P-384, P-521). لقد أثيرت شكوك في الماضي حول بعض المنحنيات القياسية، مثل منحنى Dual_EC_DRBG الذي يشتبه في أنه يحتوي على باب خلفي (Backdoor) زرعته وكالة الأمن القومي الأمريكية (NSA)، مما يؤكد على أهمية الشفافية والتدقيق في عملية اختيار المنحنيات. إن أمان تشفير المنحنى الإهليلجي يعتمد كلياً على جودة المنحنى المستخدم.
2. أخطاء التنفيذ: إن تعقيد تشفير المنحنى الإهليلجي يجعله عرضة لأخطاء التنفيذ البرمجي. يمكن أن تؤدي الأخطاء البسيطة في تطبيق العمليات الحسابية أو في توليد الأعداد العشوائية إلى ثغرات أمنية كارثية. على سبيل المثال، إعادة استخدام الرقم العشوائي المؤقت k في خوارزمية ECDSA يمكن أن يؤدي إلى كشف المفتاح الخاص بالكامل، وهو ما حدث في اختراق محفظة بلاي ستيشن 3 في عام 2010.
3. الهجمات الجانبية (Side-Channel Attacks): يمكن للمهاجمين تحليل معلومات غير مباشرة مثل استهلاك الطاقة، أو التوقيت الزمني للعمليات الحاسوبية، أو الإشعاع الكهرومغناطيسي الصادر عن الجهاز لاستنتاج أجزاء من المفتاح الخاص. يتطلب تطبيق تشفير المنحنى الإهليلجي بشكل آمن تقنيات دفاعية متقدمة لمقاومة هذه الأنواع من الهجمات.
4. التهديد الكمومي (Quantum Threat): التهديد الأكبر الذي يواجه تشفير المنحنى الإهليلجي (و RSA أيضاً) هو الحوسبة الكمومية. يمكن لخوارزمية شور (Shor’s Algorithm)، إذا تم تنفيذها على حاسوب كمومي قوي بما فيه الكفاية، أن تحل مسألة اللوغاريتم المتقطع للمنحنى الإهليلجي بكفاءة، مما يكسر النظام بأكمله. على الرغم من أن الحواسيب الكمومية القادرة على ذلك لا تزال نظرية إلى حد كبير، إلا أن مجتمع التشفير يعمل بجد على تطوير “التشفير ما بعد الكمومي” (Post-Quantum Cryptography – PQC)، وهي خوارزميات جديدة يُعتقد أنها آمنة ضد كل من الحواسيب الكلاسيكية والكمومية.

مستقبل تشفير المنحنى الإهليلجي

في الوقت الحاضر، يظل تشفير المنحنى الإهليلجي المعيار الذهبي للتشفير غير المتماثل. فهو يوفر توازناً مثالياً بين الأمان والكفاءة، مما يجعله مكوناً أساسياً في البنية التحتية للإنترنت، والخدمات المصرفية، والعملات المشفرة، وأجهزة إنترنت الأشياء. إن اعتماد تشفير المنحنى الإهليلجي مستمر في النمو، وهو يحل تدريجياً محل RSA في الأنظمة القديمة.

ستستمر الأبحاث في تحسين أمان وكفاءة تطبيقات تشفير المنحنى الإهليلجي، مع التركيز على تطوير منحنيات جديدة أكثر أماناً (مثل Curve25519 و Curve448) وتقنيات تنفيذ مقاومة للهجمات الجانبية. ومع ذلك، فإن السباق نحو الحوسبة الكمومية يعني أن عصر هيمنة تشفير المنحنى الإهليلجي له نهاية محتملة في الأفق البعيد. ستكون المرحلة التالية من تطور التشفير هي الانتقال التدريجي إلى خوارزميات PQC، ولكن حتى ذلك الحين، سيبقى تشفير المنحنى الإهليلجي حجر الزاوية الذي يحمي عالمنا الرقمي. إن الإرث الذي سيتركه تشفير المنحنى الإهليلجي هو إثبات أن التطور في الرياضيات المجردة يمكن أن يكون له تأثير عميق ومباشر على أمن وحياة المليارات من البشر.

خاتمة

في الختام، يمثل تشفير المنحنى الإهليلجي قفزة نوعية في تاريخ علم التشفير. من خلال استغلال بنية رياضية أنيقة ومعقدة، تمكن من تقديم حل لمشكلة لطالما واجهت التشفير غير المتماثل: الحاجة إلى مفاتيح طويلة جداً لضمان الأمان. إن تشفير المنحنى الإهليلجي قد أتاح لنا بناء أنظمة أسرع وأكثر كفاءة وأماناً، تتناسب مع متطلبات الأجهزة الحديثة، من الخوادم العملاقة إلى أصغر أجهزة الاستشعار. ورغم التحديات التي يواجهها، من أخطاء التنفيذ إلى التهديد الكمومي المستقبلي، فإن المبادئ التي أرساها تشفير المنحنى الإهليلجي ستظل تلهم الجيل القادم من حلول التشفير. لقد أثبت تشفير المنحنى الإهليلجي أنه أكثر من مجرد خوارزمية؛ إنه شهادة على القوة الكامنة في الرياضيات لحل بعض المشاكل الأكثر إلحاحاً في عصرنا التكنولوجي، وسيظل دوره محورياً في حماية خصوصيتنا وأمننا الرقمي لسنوات قادمة. إن فهم قوة ومرونة تشفير المنحنى الإهليلجي ضروري لكل مهتم بأمن المعلومات. إن التقدم الذي أحرزه تشفير المنحنى الإهليلجي لا يمكن إنكاره، فهو يمثل بحق ثورة هادئة ولكنها عميقة في عالمنا الرقمي. إن براعة تشفير المنحنى الإهليلجي تكمن في كفاءته التي لا تضاهى. وفي النهاية، يعتبر تشفير المنحنى الإهليلجي مثالاً ساطعاً على الابتكار في مجال الأمن السيبراني.

الأسئلة الشائعة

1. ما هي الميزة الأساسية التي يقدمها تشفير المنحنى الإهليلجي (ECC) مقارنة بخوارزمية RSA؟

الميزة الأساسية هي “الكفاءة الأمنية” (Security Efficiency). يوفر تشفير المنحنى الإهليلجي نفس مستوى الأمان الذي تقدمه RSA ولكن بأطوال مفاتيح أقصر بكثير. على سبيل المثال، مفتاح ECC بطول 256 بت يعادل في قوته مفتاح RSA بطول 3072 بت. هذه الكفاءة تقلل من متطلبات التخزين، واستهلاك عرض النطاق الترددي، والحمل الحسابي، مما يجعله مثالياً للبيئات محدودة الموارد مثل الأجهزة المحمولة وإنترنت الأشياء (IoT).

2. ما هي “مسألة اللوغاريتم المتقطع للمنحنى الإهليلجي” (ECDLP) التي يستند إليها أمان ECC؟

هي المشكلة الحسابية الصعبة التي تكمن في جوهر أمان ECC. رياضياً، إذا كان لدينا نقطتان على المنحنى الإهليلجي، النقطة الأساسية G ونقطة المفتاح العام Q، بحيث Q = k * G (حيث k هو المفتاح الخاص)، فإن ECDLP هي صعوبة إيجاد العدد الصحيح k بمعرفة G و Q. بينما عملية حساب Q (الضرب القياسي) سهلة، فإن العملية العكسية (إيجاد k) تعتبر مستحيلة حسابياً للمنحنيات المختارة بعناية.

3. أين يتم استخدام تشفير المنحنى الإهليلجي في تطبيقات العالم الحقيقي؟

يُستخدم ECC على نطاق واسع في العديد من التطبيقات الحيوية، أبرزها:

• بروتوكول TLS/SSL: لتأمين اتصالات الويب (HTTPS) عبر بروتوكول تبادل المفاتيح ECDH.
• العملات المشفرة: مثل بيتكوين وإيثريوم، حيث تُستخدم خوارزمية ECDSA لإنشاء التوقيعات الرقمية التي تؤمن المعاملات وتثبت ملكية الأصول.
• الرسائل المشفرة: في تطبيقات مثل Signal و WhatsApp لتوفير التشفير من طرف إلى طرف.
• إنترنت الأشياء (IoT): حيث كفاءته العالية تجعله مناسباً للأجهزة ذات القدرة الحاسوبية المحدودة.

4. هل جميع المنحنيات الإهليلجية آمنة للاستخدام في التشفير؟

لا، ليست كل المنحنيات آمنة. يجب اختيار المنحنيات ومعلماتها (Domain Parameters) بعناية فائقة لتجنب نقاط الضعف الرياضية التي قد تسهل حل مسألة ECDLP. لهذا السبب، تعتمد التطبيقات الآمنة على منحنيات قياسية تم فحصها بدقة من قبل خبراء التشفير، مثل تلك التي حددها المعهد الوطني للمعايير والتكنولوجيا (NIST) (مثل P-256) أو منحنيات حديثة مثل Curve25519.

5. كيف تشكل الحوسبة الكمومية تهديداً على تشفير المنحنى الإهليلجي؟

تشكل الحواسيب الكمومية تهديداً وجودياً لـ ECC. باستخدام “خوارزمية شور” (Shor’s Algorithm)، يمكن لحاسوب كمومي قوي بما فيه الكفاية أن يحل مسألة اللوغاريتم المتقطع للمنحنى الإهليلجي بكفاءة وفي زمن كثير حدود (polynomial time)، مما يسمح بكشف المفاتيح الخاصة وكسر النظام بالكامل. هذا التهديد دفع مجتمع التشفير إلى تطوير “التشفير ما بعد الكمومي” (PQC).

6. ما هو الفرق الجوهري بين بروتوكول ECDH وخوارزمية ECDSA؟

الفرق يكمن في وظيفتهما الأساسية:

• ECDH (Elliptic Curve Diffie-Hellman): هو بروتوكول لـ تبادل المفاتيح. يسمح لطرفين بإنشاء سر مشترك وسري عبر قناة غير آمنة، والذي يُستخدم عادةً لتشفير البيانات بشكل متماثل (مثل AES).
• ECDSA (Elliptic Curve Digital Signature Algorithm): هي خوارزمية لـ التوقيع الرقمي. تُستخدم لإثبات صحة وهوية المرسل وضمان سلامة البيانات (أنها لم تُعدل)، ولكنها لا تقوم بتشفير البيانات نفسها.

7. ما هو السبب الرياضي وراء كون مفاتيح ECC أقصر من مفاتيح RSA لنفس مستوى الأمان؟

السبب يعود إلى التعقيد الحسابي للمشكلة الأساسية لكل منهما. أفضل الخوارزميات المعروفة لحل مسألة ECDLP (التي يعتمد عليها ECC) هي خوارزميات أسية بالكامل (fully exponential). في المقابل، أفضل الخوارزميات لحل مشكلة تحليل الأعداد الصحيحة الكبيرة (التي يعتمد عليها RSA) هي خوارزميات شبه أسية (sub-exponential). هذا يعني أن صعوبة كسر ECC تزداد بشكل أسرع بكثير مع زيادة طول المفتاح مقارنة بـ RSA.

8. ما هو أخطر خطأ يمكن أن يرتكبه المطور عند تنفيذ خوارزمية ECDSA؟

أخطر خطأ هو إعادة استخدام القيمة العشوائية المؤقتة k (المعروفة باسم nonce) عند إنشاء توقيعين مختلفين بنفس المفتاح الخاص. إذا تم استخدام نفس قيمة k لتوقيع رسالتين مختلفتين، يمكن للمهاجم الذي يحصل على هذين التوقيعين أن يقوم بحل معادلتين خطيتين بسيطتين واستعادة المفتاح الخاص بالكامل، مما يؤدي إلى اختراق كامل للنظام.

9. ما هي “معلمات النطاق” (Domain Parameters) في ECC، ولماذا هي مهمة؟

هي مجموعة من البيانات العامة التي تحدد المنحنى الإهليلجي المستخدم ويجب أن يتفق عليها جميع الأطراف قبل إجراء أي عملية تشفير. تشمل هذه المعلمات: معادلة المنحنى (المعاملان a و b)، الحقل المنتهي المستخدم (مثل F_p)، النقطة الأساسية G، ورتبة n للنقطة G. أهميتها تكمن في أنها تشكل السياق الرياضي المشترك الذي تتم ضمنه جميع العمليات الحسابية، وأي اختلاف فيها سيؤدي إلى نتائج غير صحيحة وفشل الاتصال الآمن.

10. إذا كان ECC مهدداً بالحوسبة الكمومية، فما هو البديل المستقبلي؟

البديل المستقبلي هو “التشفير ما بعد الكمومي” (Post-Quantum Cryptography – PQC). وهو فرع من علم التشفير يركز على تطوير خوارزميات تشفير يُعتقد أنها آمنة ضد الهجمات من كل من الحواسيب الكلاسيكية والكمومية. تعتمد هذه الخوارزميات على مسائل رياضية مختلفة تماماً عن تحليل الأعداد أو اللوغاريتمات المتقطعة، مثل التشفير القائم على الشبيكات (Lattice-based cryptography) أو التشفير القائم على الهاش (Hash-based cryptography).