الثابت باي (π): اللغز الذي حير العلماء وسكن كل ذرة في الكون
كيف تحول رمز رياضي بسيط إلى لغز كوني لم يُحَل بعد؟

ملخص الإجابة:
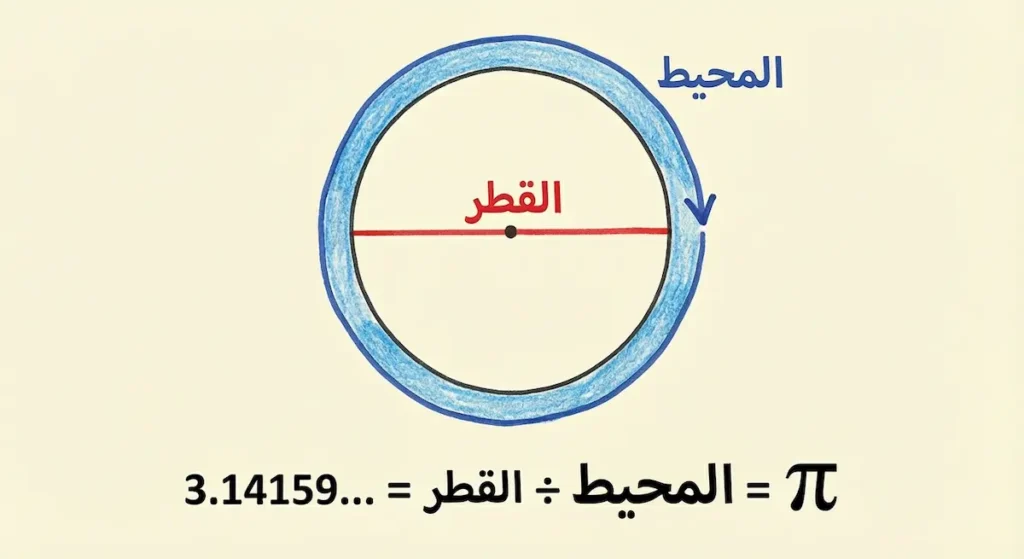
الثابت باي (Pi – π) هو النسبة الثابتة بين محيط أي دائرة وقطرها، وتساوي تقريباً 3.14159. يُعَدُّ هذا الرقم عدداً غير نسبي (Irrational Number)؛ إذ تستمر أرقامه العشرية إلى ما لا نهاية دون تكرار أو نمط. يظهر الثابت باي في الفيزياء والهندسة والطبيعة، مما يجعله أحد أهم الثوابت الرياضية في الكون.
هل توقفت يوماً أمام إطار سيارتك وتساءلت: كم يبلغ محيطه بالضبط؟ ربما حاولت القياس بشريط، لكنك لن تصل أبداً للرقم الدقيق. أنت لست وحدك في هذه الحيرة. لقد أمضى عباقرة البشرية آلاف السنين يطاردون هذا الرقم الهارب. في هذا المقال، ستكتشف أن الثابت باي ليس مجرد رقم تحفظه للامتحان، بل هو مفتاح لفهم الكون من أصغر ذرة إلى أبعد مجرة.
ما هو الثابت باي وكيف اكتشفه الإنسان؟
عندما تنظر إلى أي دائرة في هذا العالم، سواء كانت صغيرة كحبة عدس أو ضخمة كالشمس، فإن العلاقة بين محيطها وقطرها تبقى ثابتة دائماً. هذه العلاقة السحرية هي ما نسميه الثابت باي. لقد أدرك البشر هذه الحقيقة منذ فجر الحضارة.
فما هو هذا الرقم تحديداً؟ الإجابة بسيطة ومعقدة في آن واحد. الثابت باي يساوي 3.14159265358979… وهكذا إلى ما لا نهاية. نعم، لا نهاية حرفياً! فقد حسب العلماء حتى عام 2024 أكثر من 100 تريليون خانة عشرية، ولم يجدوا نهاية أو نمطاً متكرراً. هذا يجعله عدداً “غير نسبي” (Irrational Number)؛ أي أنه لا يمكن كتابته ككسر بسيط مهما حاولنا.
حقيقة مذهلة
لو كتبت أرقام الثابت باي المعروفة حالياً على ورق، ستحتاج إلى ورق يمتد من الأرض إلى القمر والعودة ملايين المرات!
كيف تم حساب قيمة الثابت باي عبر التاريخ؟
لم تكن رحلة اكتشاف الثابت باي سهلة أبداً. بدأت القصة قبل أكثر من 4000 عام، واستمرت حتى يومنا هذا مع أقوى الحواسيب الخارقة.
البابليون والمصريون: البدايات المتواضعة
في بلاد ما بين النهرين، استخدم البابليون قيمة تقريبية للثابت باي تساوي 3.125 حوالي عام 1900 قبل الميلاد. كانت هذه القيمة كافية لاحتياجاتهم اليومية في البناء والزراعة. من جهة ثانية، استخدم المصريون القدماء قيمة أدق قليلاً تساوي تقريباً 3.16، وقد ظهرت في بردية أحمس الشهيرة التي يعود تاريخها إلى 1650 قبل الميلاد.
فهل يا ترى استطاع الفراعنة بناء الأهرامات بهذه القيمة التقريبية؟ الإجابة نعم! فالفرق بين 3.16 و3.14159 لا يُحدث تأثيراً كبيراً في المباني الضخمة. لكن هذا لم يُرضِ العقول الفضولية التي أرادت الدقة المطلقة.
أرخميدس: أول محاصرة منهجية للثابت باي
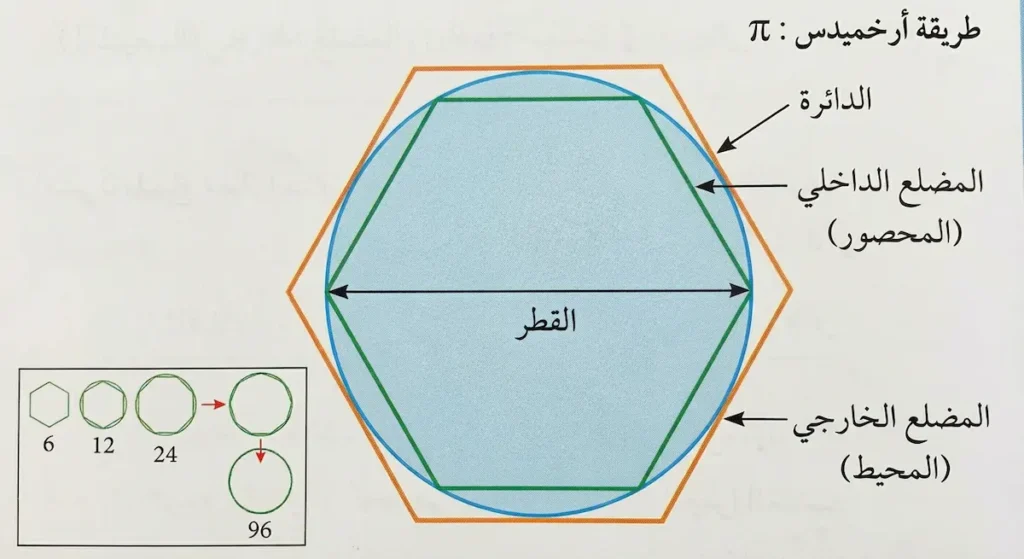
جاء أرخميدس السرقوسي (287-212 ق.م) بفكرة عبقرية غيرت مسار التاريخ. بدلاً من محاولة قياس الدائرة مباشرة، قرر “حصارها” بالمضلعات. رسم مضلعاً داخل الدائرة وآخر خارجها، ثم زاد عدد الأضلاع تدريجياً.
بدأ بالسداسي (6 أضلاع)، ثم الاثني عشري (12 ضلعاً)، واستمر حتى وصل إلى مضلع من 96 ضلعاً! وبهذه الطريقة، حدد أن الثابت باي يقع بين 223/71 و22/7. هذه الدقة المذهلة (بين 3.1408 و3.1429) ظلت الأفضل لقرون طويلة.
معلومة تاريخية
طريقة أرخميدس كانت أول خوارزمية (Algorithm) في التاريخ لحساب قيمة رياضية. يعتبره كثيرون لهذا السبب “أب الحوسبة” قبل اختراع الحاسوب بألفي عام!
العصر الذهبي الإسلامي: قفزة عملاقة نحو الدقة
هنا تأتي نقطة لا تذكرها معظم المصادر الغربية. في القرن الخامس عشر الميلادي، حقق العالم الفارسي غياث الدين جمشيد الكاشي إنجازاً استثنائياً. في كتابه “رسالة المحيطية” عام 1424، حسب الثابت باي بدقة 16 خانة عشرية!
كيف فعل ذلك بدون آلات حاسبة؟ استخدم مضلعاً من 3×2²⁸ ضلعاً (أكثر من 800 مليون ضلع نظرياً). هذا الإنجاز سبق أوروبا بقرنين كاملين. لقد كان الكاشي يعمل في مرصد سمرقند تحت رعاية الأمير أولوغ بيك، وكان دافعه حساب محيط الكون المعروف آنذاك بدقة متناهية.
الجدير بالذكر أن دقة الكاشي كانت كافية لحساب محيط دائرة بحجم الكون المرئي مع خطأ لا يتجاوز سُمك شعرة! هذا قبل 600 عام من عصر الحواسيب.

عصر الحواسيب: السباق نحو اللانهاية
مع اختراع الحاسوب في القرن العشرين، انطلق سباق محموم. في عام 1949، حسب حاسوب ENIAC الشهير 2037 خانة في 70 ساعة. وبحلول عام 2024، تجاوز الرقم القياسي 100 تريليون خانة بفضل الحوسبة السحابية (Cloud Computing).
لكن السؤال المنطقي: لماذا نحتاج كل هذه الخانات؟ الحقيقة أن الهدف العملي انتهى منذ زمن. هذه الحسابات أصبحت اختباراً لقوة الحواسيب وصحة خوارزمياتها، وليست لحاجة عملية فعلية.
| السنة | الجهة/الباحث | عدد الخانات | الحاسوب المستخدم | المدة المستغرقة |
|---|---|---|---|---|
| 1949 | جون ريتش وآخرون | 2,037 | ENIAC | 70 ساعة |
| 1973 | جان جيلود | 1,001,250 | CDC 7600 | 23.3 ساعة |
| 1989 | الأخوان تشودنوفسكي | 1,011,196,691 | IBM 3090 | عدة شهور |
| 1999 | ياسوماسا كانادا | 206,158,430,000 | Hitachi SR8000 | 37 ساعة |
| 2011 | شيغيرو كوندو | 10,000,000,000,000 | حاسوب شخصي معدّل | 371 يوماً |
| 2020 | تيموثي موليكان | 50,000,000,000,000 | حاسوب شخصي | 303 أيام |
| 2024 | مختبرات ستورجن | 105,000,000,000,000 | حوسبة سحابية | 75 يوماً |

اقرأ أيضاً: ليونارد أويلر: حياة وإرث أعظم رياضي في التاريخ
لماذا يُعَدُّ الثابت باي عدداً غير نسبي؟
هذا السؤال حير الرياضيين لقرون. الأعداد غير النسبية (Irrational Numbers) هي أعداد لا يمكن التعبير عنها بكسر بسط ومقام صحيحين. وبالتالي، فإن أرقامها العشرية لا تنتهي ولا تتكرر.
أثبت العالم الألماني يوهان لامبرت (Johann Lambert) عام 1761 أن الثابت باي غير نسبي. كان البرهان معقداً ويعتمد على الكسور المستمرة (Continued Fractions). بعده بقرن، أثبت فرديناند ليندمان عام 1882 أن الثابت باي “متسامٍ” (Transcendental)؛ أي أنه ليس حلاً لأي معادلة جبرية ذات معاملات صحيحة.
ماذا يعني هذا عملياً؟ يعني أن مسألة “تربيع الدائرة” الشهيرة مستحيلة رياضياً. حاول اليونانيون قديماً رسم مربع مساحته تساوي مساحة دائرة معينة باستخدام المسطرة والفرجار فقط. قضى كثيرون حياتهم في هذه المحاولة، ليأتي ليندمان ويثبت استحالتها تماماً.
لحظة تأمل
تخيل أنك تحاول حل لغز لا حل له أصلاً! هذا ما فعله آلاف الرياضيين لألفي عام قبل إثبات الاستحالة.
أين يظهر الثابت باي في الطبيعة والكون؟
قد تظن أن الثابت باي محصور في دروس الهندسة والدوائر. لكن الحقيقة أنه يختبئ في أماكن لا تخطر على بال، من الأنهار إلى الذرات إلى المجرات.
الأنهار: تعرجات غامضة
لاحظ العالم هانز هنريك شتولوم ظاهرة مدهشة. عندما تقيس طول نهر متعرج من المنبع إلى المصب، ثم تقيس المسافة المستقيمة بينهما، ستجد أن النسبة بين الطولين تقترب من الثابت باي!
ليس هذا صدفة. الأنهار تتعرج بسبب تفاعل معقد بين سرعة الماء وطبيعة التربة. هذا التفاعل يخلق نمطاً رياضياً يرتبط بالدوائر بطريقة غير مباشرة. الأمر يشبه توقيع الطبيعة الخفي.
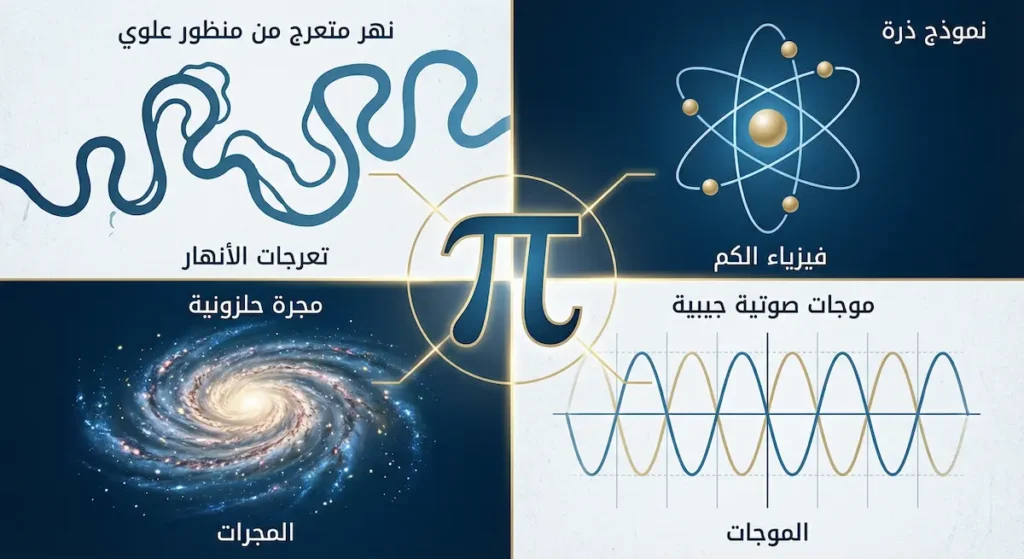
فيزياء الكم: في أصغر مكونات المادة
يظهر الثابت باي بقوة في مبدأ عدم اليقين لهايزنبرغ (Heisenberg’s Uncertainty Principle). هذا المبدأ الأساسي في ميكانيكا الكم يقول إنك لا تستطيع معرفة موقع الجسيم وسرعته معاً بدقة تامة. والعلاقة الرياضية التي تصف هذا المبدأ تحتوي على الثابت باي.
كذلك يظهر في معادلات شرودنغر التي تصف سلوك الموجات الكمية، وفي حسابات البنية الذرية. بدون الثابت باي، لن نفهم كيف تعمل الترانزستورات في هاتفك الذكي!
النسبية العامة: في أكبر هياكل الكون
معادلات أينشتاين للجاذبية (Einstein’s Field Equations) تحتوي على الثابت باي. هذه المعادلات تصف كيف ينحني الزمكان بفعل الكتلة، وهي أساس فهمنا للثقوب السوداء والانفجار العظيم.
إذاً، الثابت باي يربط أصغر جسيم بأكبر بنية كونية. هل هذا صدفة؟ يعتقد بعض الفيزيائيين أنه دليل على “وحدة الكون” الرياضية العميقة.
أغرب حقيقة في هذا المقال
رقم هاتفك، تاريخ ميلادك، وربما كل تسلسل أرقام يمكنك تخيله، موجود في مكان ما داخل خانات الثابت باي اللانهائية! هذا بناءً على فرضية “الأرقام الطبيعية” (Normal Numbers) التي لم تُثبت بعد للثابت باي، لكنها مرجحة جداً.
اقرأ أيضاً: ميكانيكا الكم: المبادئ الأساسية وتطبيقاتها
كيف تستخدم ناسا الثابت باي في استكشاف الفضاء؟
قد تتخيل أن وكالة ناسا تستخدم ملايين الخانات من الثابت باي لتوجيه مركباتها الفضائية. المفاجأة أنهم يستخدمون 15 خانة فقط!
لماذا هذا العدد القليل؟ لأن 15 خانة كافية لحساب محيط دائرة بحجم الكون المرئي بخطأ لا يتجاوز سُمك بروتون واحد. وبالتالي، فإن أي خانات إضافية تصبح بلا معنى عملي.
يستخدم مهندسو ناسا القيمة: 3.141592653589793 لحساب مسارات المركبات إلى المريخ والكواكب البعيدة. هذه الدقة مكنت مركبة “فويجر 1” من السفر مليارات الكيلومترات والوصول لأهدافها بدقة متناهية.
مثال تطبيقي من الواقع:
تخيل أنك مهندس في ناسا وتريد حساب المسافة التي ستقطعها مركبة فضائية تدور حول المريخ. قطر مدار المركبة 10,000 كيلومتر. كيف تحسب المحيط؟
- المحيط = الثابت باي × القطر
- المحيط = 3.141592653589793 × 10,000
- المحيط = 31,415.92653589793 كيلومتر
بهذه البساطة، تعرف المسافة الدقيقة لدورة كاملة. والخطأ الناتج عن استخدام 15 خانة بدلاً من تريليون خانة؟ أقل من جزء من المليار من الملليمتر!

اقرأ أيضاً: كوكب المريخ: الخصائص، الاستكشاف، ومستقبل البشر
كيف يحفظ بعض الناس آلاف خانات الثابت باي؟
في عام 2015، حطم الهندي راجفير مينا الرقم القياسي العالمي بحفظ 70,000 خانة من الثابت باي! استغرق تسميعها 10 ساعات متواصلة.
فما هي الطرق المستخدمة لهذا الإنجاز الخارق؟
تقنيات الحفظ الشائعة:
- قصر الذاكرة (Memory Palace): تحويل الأرقام إلى صور ذهنية وربطها بأماكن مألوفة في منزلك أو مدينتك.
- الترميز الصوتي (Phonetic System): تحويل كل رقم إلى صوت ساكن، ثم تكوين كلمات وجمل سهلة الحفظ.
- التقسيم (Chunking): تقسيم الأرقام إلى مجموعات صغيرة (3-4 أرقام) وحفظ كل مجموعة كوحدة مستقلة.
- القصص المترابطة: ربط كل مجموعة أرقام بحدث في قصة خيالية متسلسلة.
هل سمعت من قبل بـ “عيد الباي” (Pi Day)؟ يُحتفل به في 14 مارس (3/14 بالتقويم الأمريكي) تكريماً لهذا الرقم العجيب. في هذا اليوم، تُقام مسابقات لحفظ أكبر عدد من الخانات حول العالم.
ما هو الفرق بين الثابت باي وتاو؟

في عام 2010، أثار عالم الرياضيات مايكل هارتل جدلاً كبيراً. اقترح استبدال الثابت باي بثابت جديد سماه “تاو” (Tau – τ)، وهو ببساطة ضعف الثابت باي (τ = 2π ≈ 6.28318).
ما حجة هارتل؟ يرى أن تاو أكثر “طبيعية” لأنه يمثل النسبة بين المحيط ونصف القطر (وليس القطر الكامل). وبما أن نصف القطر أكثر استخداماً في الرياضيات من القطر، فإن تاو سيُبسط معادلات كثيرة.
على سبيل المثال:
- الدائرة الكاملة = 360 درجة = 2π راديان = τ راديان
- مع تاو، تصبح الدائرة الكاملة ببساطة “τ واحد”
على النقيض من ذلك، يدافع المحافظون عن الثابت باي بأنه مترسخ في آلاف السنين من التاريخ، ولا داعي لتغييره. الجدل مستمر حتى اليوم، وقد ظهر “يوم تاو” (28 يونيو = 6/28) كمنافس ليوم الباي!
للتفكير
هل تظن أن تغيير ثابت رياضي عمره آلاف السنين أمر منطقي، حتى لو كان البديل “أجمل” رياضياً؟
كيف تحسب الثابت باي بنفسك باستخدام البرمجة؟
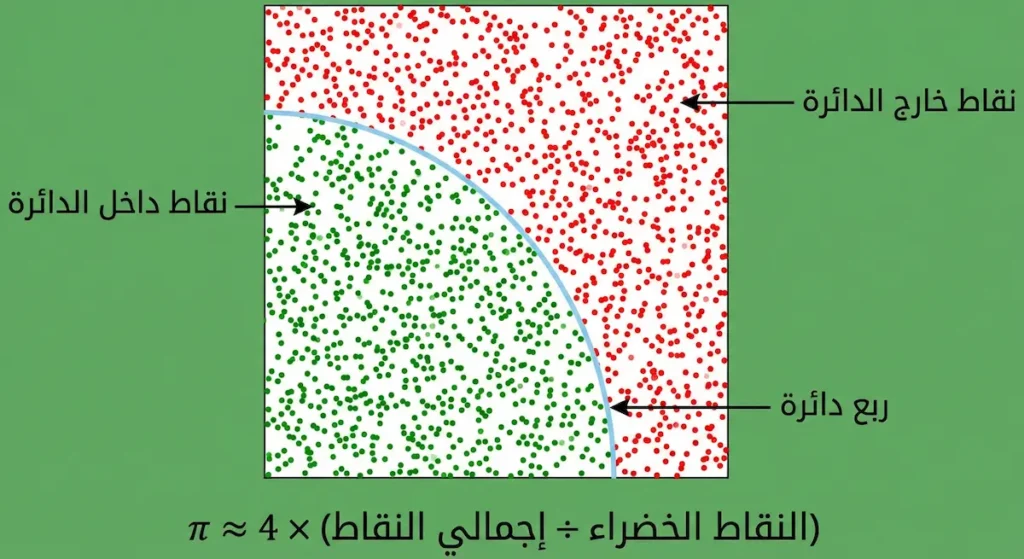
إليك تجربة عملية ممتعة. باستخدام طريقة “مونت كارلو” (Monte Carlo Method)، يمكنك تقدير قيمة الثابت باي باستخدام العشوائية!
الفكرة ببساطة:
تخيل مربعاً طول ضلعه 1، وبداخله ربع دائرة نصف قطرها 1. لو أمطرت السماء نقاطاً عشوائية على هذا المربع، فإن نسبة النقاط التي تقع داخل ربع الدائرة إلى إجمالي النقاط ستقترب من (π/4).
الكود بلغة بايثون (Python):
import random
total_points = 1000000
inside_circle = 0
for _ in range(total_points):
x = random.uniform(0, 1)
y = random.uniform(0, 1)
if x**2 + y**2 <= 1:
inside_circle += 1
pi_estimate = 4 * inside_circle / total_points
print(f"قيمة الثابت باي التقريبية: {pi_estimate}")
شرح الكود خطوة بخطوة:
- نرمي مليون نقطة عشوائية داخل المربع
- نحسب كم نقطة وقعت داخل ربع الدائرة (المسافة من المركز ≤ 1)
- نضرب النسبة في 4 لنحصل على تقدير الثابت باي
جرب تشغيل الكود عدة مرات. ستحصل على قيم قريبة من 3.14، لكنها تختلف قليلاً كل مرة بسبب العشوائية. كلما زاد عدد النقاط، زادت الدقة.
تحدٍّ للمبرمجين
حاول تعديل الكود لاستخدام متسلسلة لايبنتز (Leibniz Series) بدلاً من مونت كارلو. الصيغة: π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
اقرأ أيضاً: نظرية الاحتمالات: الأساس، القواعد، والتطبيقات
ما هي أغرب الحقائق عن الثابت باي؟
جمعتُ لك مجموعة من الحقائق المدهشة التي ستغير نظرتك لهذا الرقم:
حقائق رياضية:
- صيغة أويلر: المعادلة e^(iπ) + 1 = 0 تربط خمسة من أهم الثوابت الرياضية (e, i, π, 1, 0) في علاقة واحدة. يعتبرها كثيرون “أجمل معادلة في التاريخ”.
- مسألة بازل: مجموع 1 + 1/4 + 1/9 + 1/16 + … (مقلوب مربعات الأعداد الطبيعية) يساوي π²/6. اكتشفها أويلر عام 1735.
- إبرة بوفون: إذا ألقيت إبرة طولها L على أرضية مخططة بخطوط متوازية المسافة بينها L، فإن احتمال أن تقطع الإبرة خطاً يساوي 2/π!
حقائق تاريخية وثقافية:
- قبر لودولف: العالم الألماني لودولف فان سويلن (Ludolph van Ceulen) قضى 25 عاماً من حياته يحسب 35 خانة من الثابت باي. نُقشت هذه الأرقام على شاهد قبره تخليداً لإنجازه.
- قانون إنديانا: في عام 1897، كادت ولاية إنديانا الأمريكية تُصدر قانوناً يجعل الثابت باي يساوي 3.2 رسمياً! لحسن الحظ، تدخل عالم رياضيات وأوقف هذه الكارثة.
- الرقم القياسي للحساب: في يونيو 2024، حسب الباحثون في مختبرات ستورجن (Storgeon Labs) أكثر من 105 تريليون خانة باستخدام الحوسبة السحابية.
كيف يرتبط الثابت باي بالواقع العربي والتعليم؟
في المناهج العربية، غالباً ما يُقدَّم الثابت باي كرقم جامد للحفظ دون شرح أهميته الحقيقية. يحفظ الطلاب أن π ≈ 22/7 أو 3.14، لكنهم نادراً ما يفهمون لماذا هذا الرقم موجود أصلاً.
هذا يخلق فجوة بين الرياضيات والواقع. الطالب يرى الثابت باي كعبء للحفظ، لا كأداة لفهم العالم. من جهة ثانية، تُغفل المناهج غالباً الإسهام العربي والإسلامي الضخم في تاريخ هذا الثابت.
هل تعلم أن الخوارزمي (780-850م) ناقش الثابت باي في كتابه عن الجبر؟ وأن علماء بيت الحكمة في بغداد طوروا طرقاً لحسابه بدقة أكبر؟ هذا التراث العلمي يستحق أن يُدرَّس بفخر في مدارسنا.
نصائح للطلاب العرب:
لا تحفظ الثابت باي، بل افهمه. جرب أن تقيس محيط أي جسم دائري (طبق، غطاء، عجلة) ثم اقسمه على القطر. ستحصل دائماً على قيمة قريبة من 3.14. هذه التجربة البسيطة ستجعل الرقم حقيقياً في ذهنك.
كذلك، تعلم البرمجة واستخدمها لاستكشاف الثابت باي. الكود الذي عرضته سابقاً يمكنك تشغيله على أي حاسوب. ستشعر بمتعة الاكتشاف بدلاً من جفاف الحفظ.
اقرأ أيضاً: تعلم الرياضيات: التحديات، الاستراتيجيات، والموارد
هل أرقام الثابت باي عشوائية حقاً؟
هذا سؤال يؤرق علماء الرياضيات منذ عقود. الظاهر أن أرقام الثابت باي تتوزع عشوائياً؛ كل رقم من 0 إلى 9 يظهر بنسبة متقاربة (حوالي 10% لكل رقم).
لكن هل هي “طبيعية” (Normal Number) بالمعنى الرياضي الدقيق؟ العدد الطبيعي هو الذي تظهر فيه كل سلسلة أرقام ممكنة بالتساوي على المدى الطويل. حتى الآن، لم يستطع أحد إثبات أو نفي أن الثابت باي طبيعي!
ماذا يعني هذا عملياً؟ إذا كان الثابت باي طبيعياً، فإن كل تسلسل أرقام يمكنك تخيله موجود فيه:
- رقم هاتفك
- تاريخ ميلادك
- شفرة حسابك البنكي
- نص هذا المقال إذا حُوِّل إلى أرقام
- كل كتاب كُتب أو سيُكتب!
هذه الفكرة مثيرة فلسفياً، لكنها تبقى فرضية غير مثبتة. البحث مستمر في هذا المجال، وقد يأتي يوم نعرف فيه الإجابة القاطعة.
تأمل فلسفي
إذا كان كل شيء مكتوباً في الثابت باي، فهل هذا يعني أن الكون “مُبرمج” مسبقاً؟ أم أن هذا مجرد وهم ناتج عن طبيعة الأعداد اللانهائية؟
ما هي تطبيقات الثابت باي في الحياة اليومية؟
قد تظن أنك لا تستخدم الثابت باي في حياتك. لكن الحقيقة أنه مختبئ في كل مكان حولك.
في هاتفك الذكي:
معالج هاتفك يعتمد على ترانزستورات تعمل وفق قوانين ميكانيكا الكم. هذه القوانين تحتوي على الثابت باي. بدونه، لن تعمل الإلكترونيات كما نعرفها.
في GPS والملاحة:
نظام تحديد المواقع (GPS) يحسب المسافات على سطح الأرض الكروي. هذه الحسابات تستخدم الثابت باي بشكل أساسي لأن الأرض (تقريباً) كرة.
في الموسيقى:
الموجات الصوتية تُوصف رياضياً بدوال الجيب وجيب التمام (Sine & Cosine). هذه الدوال مبنية على الثابت باي. عندما تستمع لأغنية، أذنك تستقبل موجات “باي-ية”!
في الطب:
أجهزة الرنين المغناطيسي (MRI) تعتمد على تحويل فورييه (Fourier Transform) الذي يحتوي على الثابت باي. هذه التقنية تنقذ حياة ملايين المرضى سنوياً.
| المجال | التطبيق | كيف يُستخدم الثابت باي | الدقة المطلوبة |
|---|---|---|---|
| 📱 الهواتف الذكية |
معالجة الإشارات الرقمية | تحويل فورييه للصوت والصورة | 10-15 خانة |
| 🛰️ الملاحة GPS |
حساب المسافات على سطح الأرض | معادلات الدائرة الكبرى | 15 خانة |
| 🏥 الطب |
أجهزة الرنين المغناطيسي MRI | تحويل فورييه لإعادة بناء الصور | 15-20 خانة |
| 🚀 الفضاء |
توجيه المركبات الفضائية | حساب المدارات والمسارات | 15 خانة |
| 🏛️ الهندسة المعمارية |
تصميم القباب والأقواس | حسابات المحيط والمساحة | 5-10 خانات |
| 🎵 الموسيقى الرقمية |
تخليق الموجات الصوتية | دوال الجيب وجيب التمام | 10 خانات |
| 🎮 الألعاب ثلاثية الأبعاد |
محركات الفيزياء والرسوميات | حسابات الدوران والإسقاط | 7-10 خانات |
| 🔐 التشفير |
خوارزميات الأمان | توليد الأعداد العشوائية | متغيرة |
كيف تطورت طرق حساب الثابت باي عبر العصور؟
لفهم عظمة هذا الثابت، دعنا نستعرض تطور طرق حسابه:
الطرق الهندسية (القديمة):
- طريقة المضلعات: استخدمها أرخميدس والكاشي. بطيئة لكنها دقيقة.
- طريقة الكسور المستمرة: طورها علماء الهند والعالم الإسلامي.
الطرق التحليلية (الحديثة):
- متسلسلة لايبنتز (1674): π/4 = 1 – 1/3 + 1/5 – 1/7 + … بسيطة لكنها بطيئة جداً.
- متسلسلة ماتشين (1706): أسرع بكثير، استخدمها وليام شانكس لحساب 707 خانة يدوياً (بخطأ في الخانة 528!).
- خوارزمية تشودنوفسكي (1989): الأسرع حالياً، تضيف 14 خانة صحيحة لكل حد في المتسلسلة.
الطرق الإحصائية:
- طريقة مونت كارلو: ممتعة لكنها غير عملية للدقة العالية.
- إبرة بوفون: تجربة فيزيائية حقيقية يمكن إجراؤها.
| الطريقة | المخترع/العصر | مبدأ العمل | سرعة التقارب | مستوى التعقيد | الاستخدام الحالي |
|---|---|---|---|---|---|
| المضلعات | أرخميدس (250 ق.م) | هندسي – حصر الدائرة | بطيئة جداً | منخفض | تعليمي فقط |
| متسلسلة لايبنتز | لايبنتز (1674م) | تحليلي – جمع لانهائي | بطيئة جداً | منخفض | تعليمي فقط |
| متسلسلة ماتشين | ماتشين (1706م) | تحليلي – دوال مثلثية | متوسطة | متوسط | نادر |
| خوارزمية غاوس-لوجوندر | غاوس (1809م) | تحليلي – تكراري | سريعة | مرتفع | أرقام قياسية سابقة |
| خوارزمية تشودنوفسكي | الأخوان تشودنوفسكي (1989م) | تحليلي – صيغة رامانوجان | سريعة جداً ⭐ | مرتفع جداً | الأرقام القياسية الحالية ✓ |
| مونت كارلو | متعدد (القرن 20) | إحصائي – عشوائي | بطيئة جداً | منخفض | تعليمي وترفيهي |
معلومة للمبرمجين
خوارزمية تشودنوفسكي هي المستخدمة في معظم الأرقام القياسية الحديثة. تعتمد على صيغة معقدة تتضمن مضروب الأعداد والأسس الكبيرة.
اقرأ أيضاً: علم الإحصاء: الأدوات، المنهجيات، ودوره في صنع القرار
الأسئلة الشائعة
اختار العالم الويلزي ويليام جونز عام 1706 الحرف اليوناني π لتمثيل هذا الثابت، وهو الحرف الأول من الكلمة اليونانية περιφέρεια التي تعني المحيط. لاحقاً، ساهم عالم الرياضيات الشهير ليونهارد أويلر في نشر هذا الرمز على نطاق واسع من خلال أعماله الغزيرة في القرن الثامن عشر.
يظهر الثابت باي في جميع الأبعاد دون استثناء. في الفضاء ثلاثي الأبعاد يدخل في حساب مساحة سطح الكرة وحجمها، وفي الأبعاد الأعلى يظهر في صيغ الكرات الفائقة والتكاملات متعددة الأبعاد. القاعدة العامة أن أي فضاء يحتوي على انحناءات أو دورانات سيتضمن الثابت باي في معادلاته.
القيمة 22/7 تساوي تقريباً 3.142857 وهي أدق من 3.14 بفارق ضئيل، لكن كلتيهما تقريب. الفرق بين 22/7 والقيمة الحقيقية يبلغ حوالي 0.04% بينما الفرق مع 3.14 يبلغ حوالي 0.05%. للحسابات اليومية البسيطة كلتاهما كافية، أما للتطبيقات الهندسية الدقيقة فيُستخدم 3.14159 على الأقل.
هذا مستبعد جداً من الناحية الرياضية. إثبات لامبرت عام 1761 أكد أن الثابت باي عدد غير نسبي، وهذا يعني بالضرورة أن أرقامه لا تتكرر بنمط دوري. كذلك أثبت ليندمان أنه عدد متسامٍ، مما يستبعد وجود أي بنية جبرية خفية. لكن البحث عن خصائص إحصائية معينة مثل التوزيع المتساوي للأرقام لا يزال مفتوحاً.
الآلات الحاسبة محدودة بعدد الخانات التي يمكنها تخزينها ومعالجتها، وتتراوح عادة بين 10 و15 خانة عشرية. هذه الدقة أكثر من كافية لجميع التطبيقات العملية، إذ أن الخطأ الناتج أصغر من أن يؤثر في أي قياس فيزيائي ممكن.
يرتبط الثابتان بعلاقة عميقة تظهر في صيغة أويلر الشهيرة حيث يكون مجموع الواحد مع ناتج رفع الثابت e للأس المركب الذي يتضمن باي مساوياً للصفر. كذلك يظهران معاً في التوزيع الطبيعي في الإحصاء وفي تحويل فورييه وفي معادلات ميكانيكا الكم. هذا الترابط يشير إلى وحدة عميقة في البنية الرياضية للكون.
الثابت باي ثابت رياضي مجرد ينبع من تعريف الدائرة في الهندسة الإقليدية المسطحة. في أي كون يتبع هذه الهندسة ستكون القيمة ذاتها. لكن في الفضاءات المنحنية كسطح الكرة أو الفضاء الزائدي تختلف النسبة بين المحيط والقطر عن باي، وهذا ليس تغيراً في باي بل تغير في طبيعة الهندسة نفسها.
الراديان وحدة طبيعية للزوايا لأنه يربط مباشرة بين طول القوس ونصف القطر. الدائرة الكاملة تساوي 2π راديان لأن محيط الدائرة يساوي 2π مضروباً في نصف القطر. استخدام الراديان يُبسط كثيراً من المعادلات في التفاضل والتكامل والفيزياء، بينما تُعد الدرجات وحدة اصطلاحية تاريخية مبنية على نظام الستينيات البابلي.
لا توجد صيغة مغلقة بسيطة تعطي القيمة الدقيقة بعمليات حسابية محدودة. جميع الصيغ المعروفة إما متسلسلات لانهائية أو تكاملات أو جداءات لانهائية. هذا نتيجة مباشرة لكون الثابت باي عدداً متسامياً. أقرب ما يوجد للصيغة المغلقة هو التعريف الهندسي نفسه وهو نسبة المحيط إلى القطر.
تُستخدم أرقام الثابت باي أحياناً كمصدر لتوليد أعداد شبه عشوائية في بعض خوارزميات التشفير، نظراً لعشوائية توزيع أرقامه الظاهرية. كما تظهر الدوال المثلثية المبنية على باي في خوارزميات تحويل فورييه المستخدمة في تشفير الإشارات. لكن الاستخدام الأساسي يبقى في الخوارزميات الرياضية التي تعتمد على نظرية الأعداد والمنحنيات الإهليلجية.
خاتمة: لماذا يستحق الثابت باي كل هذا الاهتمام؟
وصلنا إلى نهاية رحلتنا مع هذا الرقم العجيب. لكن الثابت باي لا ينتهي أبداً، لا حرفياً ولا مجازياً.
هذا الرقم ليس اختراعاً بشرياً، بل اكتشاف. لو قابلنا حضارة فضائية في أقصى المجرة، قد لا يفهمون لغتنا أو موسيقانا أو فنوننا. لكنهم حتماً يعرفون الثابت باي. هذا الثابت كوني بالمعنى الحرفي؛ إذ يسري في كل دائرة وموجة وذرة في الوجود.
من البابليين الذين خطوا أولى التقريبات على ألواح الطين، إلى الكاشي الذي تفوق على عصره بقرون، إلى الحواسيب الخارقة التي تطارد تريليونات الخانات، ظلت البشرية مفتونة بهذا اللغز. وسنبقى كذلك.
الجدير بالذكر أن فهم الثابت باي ليس ترفاً أكاديمياً. إنه باب لفهم الطبيعة والتكنولوجيا والكون. كل طالب يحفظ 3.14 دون فهم يُضيع فرصة للإعجاب بأحد أعظم ألغاز الرياضيات.
فهل ستنظر للدوائر من حولك بعين مختلفة بعد الآن؟
إشعار المصداقية والمراجعة:
🔍 إشعار المصداقية والمراجعة
جرت مراجعة هذا المقال من قِبَل فريق التحرير في موسوعة خلية العلمية لضمان الدقة والمعلومة الصحيحة.
المعلومات الواردة تستند إلى مصادر أكاديمية وعلمية موثوقة، وتهدف للتثقيف العام وليس كبديل عن المراجع المتخصصة. راجع قسم المصادر والمراجع في نهاية المقالة للاطلاع على المراجع الكاملة.
إذا وجدت هذا المقال مفيداً، شاركه مع أصدقائك المهتمين بالرياضيات والعلوم. ولا تنسَ تجربة كود بايثون بنفسك! الرياضيات تصبح ممتعة عندما تتحول من حفظ إلى تجربة. اكتب في التعليقات: كم خانة من الثابت باي تستطيع حفظها؟
المصادر والمراجع
الدراسات والأوراق البحثية:
- Bailey, D. H., & Borwein, J. M. (2021). Pi: The Next Generation. Springer.
https://doi.org/10.1007/978-3-030-83867-1
دراسة شاملة عن تاريخ حساب الثابت باي والخوارزميات الحديثة. - Arndt, J., & Haenel, C. (2006). Pi Unleashed. Springer-Verlag.
https://doi.org/10.1007/978-3-642-56735-3
مرجع تقني يشرح طرق الحساب المختلفة للثابت باي. - Berggren, L., Borwein, J., & Borwein, P. (2004). Pi: A Source Book. Springer.
https://doi.org/10.1007/978-1-4757-4217-6
مجموعة من النصوص التاريخية الأصلية عن الثابت باي. - Chudnovsky, D. V., & Chudnovsky, G. V. (1989). The Computation of Classical Constants. Proceedings of the National Academy of Sciences, 86(21), 8178-8182.
https://doi.org/10.1073/pnas.86.21.8178
الورقة الأصلية لخوارزمية تشودنوفسكي الأسرع لحساب الثابت باي. - Stolum, H. H. (1996). River Meandering as a Self-Organization Process. Science, 271(5256), 1710-1713.
https://doi.org/10.1126/science.271.5256.1710
الدراسة التي اكتشفت علاقة تعرج الأنهار بالثابت باي. - Bailey, D. H. (2019). The Quest for Pi. Mathematical Intelligencer, 41, 37-42.
https://doi.org/10.1007/s00283-018-9869-5
مراجعة حديثة لتاريخ البحث عن قيمة الثابت باي.
الجهات الرسمية والمنظمات:
- NASA/JPL. How Many Decimals of Pi Do We Really Need?
https://www.jpl.nasa.gov/edu/news/2016/3/16/how-many-decimals-of-pi-do-we-really-need/
شرح ناسا لعدد الخانات المستخدمة فعلياً في الملاحة الفضائية. - MIT OpenCourseWare. Single Variable Calculus – Pi.
https://ocw.mit.edu/courses/mathematics/
مصادر تعليمية من معهد ماساتشوستس للتكنولوجيا. - MacTutor History of Mathematics. Pi Through the Ages.
https://mathshistory.st-andrews.ac.uk/HistTopics/Pi_through_the_ages/
أرشيف تاريخي شامل من جامعة سانت أندروز. - Guinness World Records. Most Pi Digits Memorised.
https://www.guinnessworldrecords.com/world-records/most-pi-places-memorised
السجلات الرسمية لحفظ خانات الثابت باي. - Wolfram MathWorld. Pi Formulas.
https://mathworld.wolfram.com/PiFormulas.html
موسوعة رياضية شاملة عن صيغ حساب الثابت باي.
الكتب والموسوعات العلمية:
- Beckmann, P. (1971). A History of Pi. St. Martin’s Press.
كتاب كلاسيكي يروي تاريخ الثابت باي بأسلوب سردي ممتع. - Posamentier, A. S., & Lehmann, I. (2004). Pi: A Biography of the World’s Most Mysterious Number. Prometheus Books.
سيرة شاملة للثابت باي من المنظور الثقافي والعلمي. - Blatner, D. (1999). The Joy of Pi. Walker & Company.
كتاب ممتع للقارئ العام عن عجائب الثابت باي.
مقالات علمية مبسطة:
- Scientific American. (2024). The Enduring Mystery of Pi.
https://www.scientificamerican.com/article/pi/
مقال تبسيطي حديث عن أسرار الثابت باي.
قراءات إضافية ومصادر للتوسع
للطلاب والباحثين الراغبين في التعمق أكثر:
1. Dunham, W. (1999). Euler: The Master of Us All. Mathematical Association of America.
لماذا نقترح عليك قراءته؟ هذا الكتاب يشرح إسهامات أويلر الهائلة في فهم الثابت باي، بما فيها صيغة أويلر الشهيرة التي تربط باي بالأعداد المركبة. أسلوب سردي ممتع يناسب من أنهى المرحلة الثانوية.
2. Eymard, P., & Lafon, J. P. (2004). The Number Pi. American Mathematical Society.
لماذا نقترح عليك قراءته؟ مرجع أكاديمي متقدم يغطي الجوانب التحليلية للثابت باي، مثل إثبات لامبرت لعدم نسبيته وإثبات ليندمان لتساميه. مناسب لطلاب الرياضيات الجامعيين.
3. Borwein, J., & Bailey, D. (2008). Mathematics by Experiment: Plausible Reasoning in the 21st Century. A K Peters.
لماذا نقترح عليك قراءته؟ يستكشف كيف غيرت الحوسبة طريقة اكتشاف الحقائق الرياضية، مع أمثلة كثيرة عن الثابت باي. يفتح آفاقاً جديدة لفهم العلاقة بين الرياضيات والتجربة.
آخر تحديث: يناير 2026
تنبيه وإخلاء مسؤولية
المعلومات الواردة في هذا المقال مُقدَّمة من موسوعة خلية العلمية لأغراض تعليمية وتثقيفية عامة فقط. على الرغم من حرصنا على الدقة والتحقق من المصادر العلمية، فإن هذا المحتوى لا يُغني عن المراجع الأكاديمية المتخصصة أو الاستشارة مع خبراء في مجال الرياضيات والعلوم.
القيم والأرقام القياسية المذكورة صحيحة وفقاً لآخر تحديث للمقالة، وقد تتغير مع استمرار الأبحاث والاكتشافات العلمية. نوصي القراء بالرجوع إلى المصادر الأصلية المذكورة في قسم المراجع للتعمق أكثر.





