الحركة الدائرية: دليل شامل لفهم أساسياتها وتطبيقاتها العملية

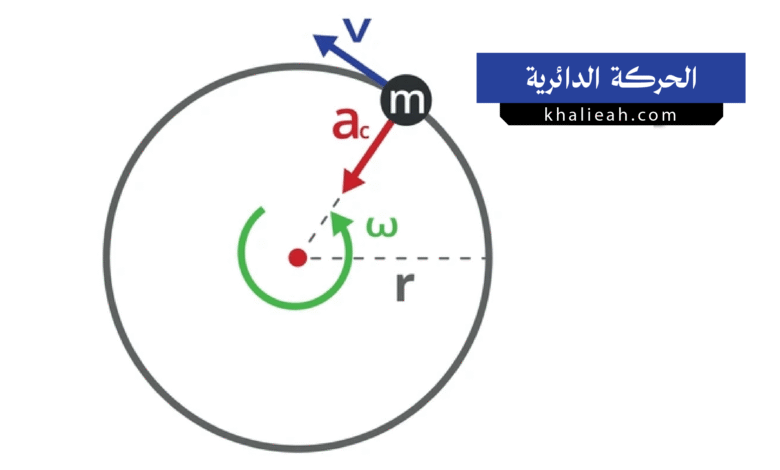
تمثل الحركة الدائرية واحدة من أكثر أنماط الحركة انتشاراً في الكون من حولنا، حيث نجدها في كل مكان بدءاً من دوران الأرض حول محورها وصولاً إلى حركة عقارب الساعة. إن فهم هذا النوع من الحركة يفتح أمامنا آفاقاً واسعة لاستيعاب العديد من الظواهر الطبيعية والتطبيقات التكنولوجية التي نستخدمها يومياً.

يعد موضوع الحركة الدائرية من المواضيع الجوهرية في علم الفيزياء، حيث يجمع بين المفاهيم النظرية والتطبيقات العملية بطريقة فريدة. تتجلى أهمية دراسة هذا الموضوع في كونه يساعدنا على فهم آليات عمل الآلات المختلفة والأجهزة التي نعتمد عليها في حياتنا اليومية. من الغسالات إلى السيارات، ومن المراوح إلى الأقمار الصناعية، جميعها تعتمد على مبادئ الحركة الدائرية في عملها. كما أن فهم هذه الحركة يمكننا من تفسير العديد من الظواهر الطبيعية مثل دوران الكواكب حول الشمس وحركة الأعاصير والرياح الدوامة، مما يعزز من قدرتنا على التعامل مع البيئة المحيطة بنا بشكل أفضل وأكثر وعياً.

مفهوم الحركة الدائرية وأساسياتها الفيزيائية

تعرف الحركة الدائرية (Circular Motion) بأنها حركة جسم على مسار دائري حول نقطة ثابتة تسمى المركز، حيث تبقى المسافة بين الجسم المتحرك والمركز ثابتة طوال فترة الحركة. هذا النوع من الحركة يتميز بخصائص فريدة تميزه عن أنواع الحركة الأخرى كالحركة المستقيمة أو الحركة المنحنية غير المنتظمة. في الحركة الدائرية، يتغير اتجاه سرعة الجسم باستمرار حتى لو ظلت قيمتها ثابتة، وهذا التغير المستمر في الاتجاه هو ما يميز هذه الحركة ويجعلها تتطلب وجود قوة مستمرة تؤثر على الجسم لإبقائه في مساره الدائري.

تتطلب الحركة الدائرية وجود نظام إحداثيات مناسب لوصفها بدقة، وغالباً ما يستخدم الفيزيائيون الإحداثيات القطبية أو الإحداثيات الزاوية لتسهيل التعامل مع المعادلات الرياضية المرتبطة بها. يمكن تصنيف هذه الحركة إلى نوعين رئيسين بناءً على ثبات السرعة الزاوية: الحركة الدائرية المنتظمة والحركة الدائرية غير المنتظمة، ولكل منهما خصائص ومعادلات رياضية خاصة تحكمها.

تعتبر دراسة الحركة الدائرية أساسية لفهم العديد من المفاهيم العلمية المتقدمة في الفيزياء والهندسة. فالحركة الدائرية ليست مجرد موضوع نظري، بل هي أساس للعديد من التطبيقات العملية التي نواجهها يومياً. من خلال فهم المبادئ الأساسية لهذه الحركة، يمكننا تصميم أنظمة ميكانيكية أكثر كفاءة وأماناً، وتحليل سلوك الأجسام المتحركة في مسارات دائرية بدقة عالية.

أنواع الحركة الدائرية وخصائصها المميزة

الحركة الدائرية المنتظمة (Uniform Circular Motion) هي النوع الذي يتحرك فيه الجسم بسرعة خطية ثابتة المقدار على طول محيط الدائرة، بينما تتغير سرعته الاتجاهية باستمرار. في هذا النوع من الحركة الدائرية، يقطع الجسم أقواساً متساوية في فترات زمنية متساوية، مما يعني أن السرعة الزاوية تبقى ثابتة. من الأمثلة الشائعة على الحركة الدائرية المنتظمة حركة عقارب الساعة ودوران الأقراص المدمجة في مشغل الأقراص بسرعة ثابتة، حيث تحافظ هذه الأجسام على سرعة دوران منتظمة دون تسارع أو تباطؤ.

أما الحركة الدائرية غير المنتظمة (Non-uniform Circular Motion)، فهي تلك التي تتغير فيها السرعة الخطية أو السرعة الزاوية للجسم أثناء حركته على المسار الدائري. في هذه الحالة، لا يكون التسارع مركزياً فقط، بل يوجد أيضاً تسارع مماسي يعمل على تغيير مقدار السرعة. من أمثلة الحركة الدائرية غير المنتظمة حركة الأراجيح الدوارة في الملاهي عند بدء تشغيلها أو إيقافها، وحركة السيارة التي تسير في منعطف دائري بينما تزيد أو تقلل من سرعتها.

يتطلب فهم كلا النوعين من الحركة الدائرية معرفة قوية بأساسيات القياس والتحليل الفيزيائي. في الحركة الدائرية المنتظمة، يكون التسارع موجهاً دائماً نحو المركز ويسمى التسارع المركزي، بينما في الحركة غير المنتظمة يوجد مكونان للتسارع: التسارع المركزي الذي يغير اتجاه السرعة، والتسارع المماسي الذي يغير مقدار السرعة.

القوانين الفيزيائية الحاكمة للحركة الدائرية

تخضع الحركة الدائرية لمجموعة من القوانين الفيزيائية التي تحكم سلوك الأجسام المتحركة في مسارات دائرية. يعد قانون نيوتن الثاني للحركة من أهم هذه القوانين، حيث ينص على أن القوة المحصلة المؤثرة على جسم تساوي حاصل ضرب كتلته في تسارعه. في حالة الحركة الدائرية، تكون هذه القوة موجهة نحو مركز الدائرة وتسمى القوة المركزية (Centripetal Force)، وهي ضرورية للحفاظ على الجسم في مساره الدائري ومنعه من الاستمرار في خط مستقيم وفقاً لقانون نيوتن الأول.

تتحدد القوة المركزية اللازمة لإبقاء جسم في حركة دائرية بالمعادلة: F = mv²/r، حيث m هي كتلة الجسم، v هي السرعة الخطية، و r هو نصف قطر المسار الدائري. تشير هذه المعادلة إلى أن القوة المركزية تتناسب طردياً مع مربع السرعة وعكسياً مع نصف القطر، مما يفسر لماذا تحتاج السيارات التي تسير بسرعات عالية إلى قوى احتكاك أكبر للبقاء على المنعطفات الدائرية. كما توضح هذه المعادلة أن المنعطفات ذات نصف القطر الأصغر تتطلب قوى مركزية أكبر للحفاظ على نفس السرعة.

تلعب قوانين الحفظ دوراً مهماً أيضاً في فهم الحركة الدائرية، خاصة قانون حفظ الزخم الزاوي الذي ينص على أن الزخم الزاوي لنظام معزول يبقى ثابتاً في غياب عزوم خارجية. هذا القانون يفسر العديد من الظواهر المرتبطة بالحركة الدائرية، مثل زيادة سرعة دوران المتزلج على الجليد عندما يسحب ذراعيه نحو جسده، حيث يقل نصف القطر فتزداد السرعة الزاوية للحفاظ على ثبات الزخم الزاوي. هذه القوانين الفيزيائية ليست مجرد معادلات رياضية، بل هي أدوات قوية لفهم وتحليل الظواهر العلمية المعقدة المرتبطة بالحركة الدائرية.

القوة المركزية والقوة الطاردة المركزية

القوة المركزية هي القوة الحقيقية التي تجذب الجسم نحو مركز الدائرة وتمنعه من الاستمرار في خط مستقيم. في الحركة الدائرية، يمكن أن تأتي هذه القوة من مصادر مختلفة حسب طبيعة الحركة والنظام المدروس. على سبيل المثال، في حالة دوران الكواكب حول الشمس، تكون القوة المركزية هي قوة الجاذبية، بينما في حالة السيارة التي تسير في منعطف دائري، تكون القوة المركزية هي قوة الاحتكاك بين الإطارات والطريق.

أما القوة الطاردة المركزية (Centrifugal Force)، فهي ليست قوة حقيقية في الواقع، بل هي قوة ظاهرية أو وهمية تنشأ من منظور مراقب يتحرك مع الجسم في الإطار المرجعي الدوار. هذه القوة الظاهرية تبدو وكأنها تدفع الجسم بعيداً عن المركز، ولكنها في الحقيقة نتيجة لميل الجسم للاستمرار في خط مستقيم وفقاً لقانون القصور الذاتي. عندما نركب في سيارة تنعطف بسرعة، نشعر بأننا ندفع نحو الخارج، وهذا الإحساس ناتج عن القوة الطاردة المركزية الظاهرية، بينما في الواقع يكون جسمنا يحاول الاستمرار في خط مستقيم.

يعد التمييز بين القوة المركزية والقوة الطاردة المركزية أمراً بالغ الأهمية لفهم الحركة الدائرية بشكل صحيح. القوة المركزية حقيقية ويمكن قياسها وتحديد مصدرها، بينما القوة الطاردة المركزية هي أثر ظاهري يعتمد على الإطار المرجعي للمراقب. في التطبيقات العملية، مثل تصميم الطرق السريعة والمنعطفات، يجب على المهندسين حساب القوة المركزية اللازمة لضمان أن تكون قوة الاحتكاك كافية لإبقاء المركبات على الطريق عند السرعات المختلفة. هذا الفهم العميق للقوى في الحركة الدائرية يساعد في تحليل البيانات المعقدة المتعلقة بالسلامة المرورية وتصميم المسارات.

السرعة الخطية والسرعة الزاوية في الحركة الدائرية

السرعة الخطية (Linear Velocity) في الحركة الدائرية تمثل المسافة التي يقطعها الجسم على محيط الدائرة في وحدة الزمن، وتقاس بوحدة متر/ثانية. هذه السرعة متجهة دائماً في اتجاه مماس لمحيط الدائرة عند كل نقطة على المسار. في الحركة الدائرية المنتظمة، يبقى مقدار السرعة الخطية ثابتاً، ولكن اتجاهها يتغير باستمرار، وهذا التغير المستمر في الاتجاه هو ما يجعل الحركة الدائرية حركة متسارعة حتى عندما تكون منتظمة.

السرعة الزاوية (Angular Velocity) تقيس معدل تغير الموضع الزاوي للجسم بالنسبة للزمن، وتقاس بوحدة راديان/ثانية أو درجة/ثانية. العلاقة بين السرعة الخطية والسرعة الزاوية تعطى بالمعادلة v = ωr، حيث v هي السرعة الخطية، ω هي السرعة الزاوية، و r هو نصف قطر الدائرة. هذه العلاقة البسيطة ولكن القوية تربط بين الكميات الخطية والكميات الزاوية في الحركة الدائرية، وتوضح أن نقاط مختلفة على جسم صلب دوار لها نفس السرعة الزاوية ولكن سرعات خطية مختلفة تعتمد على بعدها عن المركز.

تظهر أهمية فهم العلاقة بين السرعة الخطية والسرعة الزاوية في العديد من التطبيقات العملية. على سبيل المثال، في عجلة السيارة، تكون السرعة الزاوية واحدة لجميع نقاط العجلة، لكن النقاط على الحافة الخارجية لها سرعة خطية أكبر من النقاط القريبة من المركز. هذا المفهوم ضروري في تصميم التروس والبكرات وأنظمة النقل الميكانيكية المختلفة. كما أن فهم هذه العلاقة يساعد في فهم التطور الاقتصادي لصناعة المحركات والآلات الدوارة عبر الزمن.

التسارع المركزي وخصائصه في الحركة الدائرية

التسارع المركزي (Centripetal Acceleration) هو التسارع الموجه دائماً نحو مركز الدائرة، وهو المسؤول عن تغيير اتجاه السرعة في الحركة الدائرية. يحسب التسارع المركزي بالمعادلة a = v²/r أو a = ω²r، حيث يتناسب هذا التسارع طردياً مع مربع السرعة الخطية وعكسياً مع نصف القطر. حتى في الحركة الدائرية المنتظمة حيث يكون مقدار السرعة ثابتاً، يوجد تسارع مركزي بسبب التغير المستمر في اتجاه السرعة.

يعتبر التسارع المركزي أساسياً لفهم لماذا تحتاج الأجسام في حركة دائرية إلى قوة مستمرة للحفاظ على مسارها. وفقاً لقانون نيوتن الثاني، فإن وجود تسارع يتطلب وجود قوة محصلة، وهذه القوة هي القوة المركزية التي تحدثنا عنها سابقاً. كلما زادت سرعة الجسم أو قل نصف قطر المسار الدائري، زاد التسارع المركزي المطلوب، وبالتالي زادت القوة المركزية اللازمة.

في التطبيقات العملية للحركة الدائرية، يجب مراعاة التسارع المركزي بعناية لضمان السلامة والكفاءة. في تصميم الطرق السريعة مثلاً، يجب أن تكون المنعطفات بنصف قطر كافٍ لضمان أن التسارع المركزي المطلوب عند السرعات المسموحة لا يتجاوز قدرة الاحتكاك بين الإطارات والطريق. في أجهزة الطرد المركزي المستخدمة في المختبرات، يستخدم التسارع المركزي الكبير لفصل المواد ذات الكثافات المختلفة. هذه التطبيقات تتطلب فهماً دقيقاً لمفهوم التسارع المركزي وتطبيقاته في الحركة الدائرية.

تطبيقات الحركة الدائرية في المركبات والنقل

تمثل المركبات أحد أهم التطبيقات العملية للحركة الدائرية في حياتنا اليومية. عند انعطاف السيارة في منحنى دائري، فإنها تتبع مساراً دائرياً يتطلب قوة مركزية لإبقائها على الطريق. هذه القوة المركزية تأتي من قوة الاحتكاك بين إطارات السيارة والطريق، ولذلك فإن جودة الإطارات وحالة الطريق عاملان حاسمان في قدرة السيارة على الانعطاف بأمان. عندما تكون السرعة عالية جداً أو نصف قطر المنعطف صغيراً جداً، قد لا تكون قوة الاحتكاك كافية لتوفير القوة المركزية المطلوبة، مما يؤدي إلى انزلاق السيارة خارج المسار.

لتحسين أمان المركبات في المنعطفات، يستخدم المهندسون تقنية إمالة الطريق (Banking) حيث يتم رفع الحافة الخارجية للمنعطف بزاوية معينة. هذه الإمالة تساعد في توفير جزء من القوة المركزية المطلوبة من خلال مكون الوزن الموجه نحو المركز، مما يقلل الاعتماد على قوة الاحتكاك وحدها. تحسب زاوية الإمالة المثلى بناءً على نصف قطر المنعطف والسرعة المتوقعة للمركبات، وهذا يتطلب فهماً دقيقاً لمبادئ الحركة الدائرية وتطبيقها في التصميم الهندسي.

في وسائل النقل الحديثة، نجد تطبيقات متقدمة للحركة الدائرية في أنظمة التحكم الإلكترونية مثل نظام الثبات الإلكتروني (ESP) الذي يراقب حركة السيارة ويتدخل تلقائياً عند اكتشاف انحراف عن المسار المطلوب. هذه الأنظمة تستخدم حسابات معقدة تعتمد على مبادئ الحركة الدائرية لتحديد القوة المركزية المطلوبة ومقارنتها بالقوة المتاحة فعلياً. كما أن فهم الحركة الدائرية ضروري في تصميم أنظمة التعليق والتوجيه، حيث يجب أن تكون هذه الأنظمة قادرة على التعامل مع القوى الكبيرة الناتجة عن الحركة الدائرية عند السرعات العالية. يمكن ملاحظة تأثير هذه التقنيات على معدلات البطالة في صناعة السيارات حيث تتطلب تقنيات تصنيع متقدمة.

الحركة الدائرية في الألعاب الترفيهية ومدن الملاهي

التطبيقات المتنوعة في الألعاب الدوارة

تعد مدن الملاهي من أفضل الأماكن لمشاهدة تطبيقات عملية مثيرة للحركة الدائرية. تتنوع الألعاب التي تعتمد على هذا المبدأ الفيزيائي، وكل منها يوفر تجربة فريدة من نوعها:

• الدوامات الدائرية (Merry-Go-Round): هي أبسط أشكال الحركة الدائرية المنتظمة في الملاهي، حيث يدور الركاب حول محور مركزي بسرعة زاوية ثابتة. تزداد السرعة الخطية كلما ابتعدنا عن المركز، مما يفسر لماذا يشعر الركاب على الحافة الخارجية بقوة أكبر من أولئك القريبين من المركز.
• الأفعوانيات ذات الحلقات الدائرية (Loop Roller Coasters): تمثل تطبيقاً معقداً للحركة الدائرية غير المنتظمة، حيث تتغير سرعة العربة أثناء مرورها عبر الحلقة. في قمة الحلقة، يجب أن تكون السرعة كافية لضمان بقاء الركاب في مقاعدهم، حيث تعمل القوة المركزية المطلوبة على موازنة وزن العربة والركاب.
• ألعاب الكراسي الطائرة (Chair Swings): توضح كيف تؤثر السرعة الزاوية على زاوية ميل الكراسي، حيث كلما زادت سرعة الدوران، زادت القوة الطاردة المركزية الظاهرية وبالتالي زادت زاوية ميل الكراسي نحو الخارج.
• عجلات الفيريس (Ferris Wheels): على الرغم من سرعتها المنخفضة نسبياً، فإنها توفر مثالاً واضحاً للحركة الدائرية المنتظمة، حيث يشعر الركاب بتغيرات في القوة الظاهرية على أجسامهم أثناء دورانهم.

الاعتبارات الهندسية والأمان

يتطلب تصميم هذه الألعاب حسابات دقيقة للقوى المركزية والتسارعات لضمان سلامة الركاب. يجب على المهندسين مراعاة الحد الأقصى للتسارع المركزي الذي يمكن للجسم البشري تحمله دون أضرار، والذي يختلف حسب العمر والحالة الصحية. كما يجب حساب قوة المواد المستخدمة في البناء لتحمل القوى الكبيرة الناتجة عن الحركة الدائرية، خاصة في الألعاب عالية السرعة.

تستخدم أنظمة الأمان المتقدمة في هذه الألعاب مبادئ الحركة الدائرية لتصميم آليات التثبيت والفرملة. على سبيل المثال، تصمم أحزمة الأمان بحيث توفر قوة رد فعل كافية لمواجهة القوة الطاردة المركزية الظاهرية التي يشعر بها الركاب. هذه التطبيقات تتطلب معرفة عميقة بالحركة الدائرية وقوانينها، مما يجعلها مثالاً رائعاً على كيفية ترجمة المفاهيم النظرية إلى تطبيقات عملية ممتعة وآمنة.

الحركة الدائرية في الأجهزة المنزلية اليومية

الأجهزة الكهربائية الدوارة

تعتمد العديد من الأجهزة المنزلية التي نستخدمها يومياً على مبادئ الحركة الدائرية في عملها، مما يجعل فهم هذه المبادئ ضرورياً لاستخدامها بكفاءة وصيانتها بشكل صحيح:

• الغسالات الأوتوماتيكية: تستخدم الحركة الدائرية في مرحلة العصر (Spin Cycle) حيث يدور الحوض بسرعة عالية جداً قد تصل إلى 1400 دورة في الدقيقة. هذه السرعة العالية تولد قوة طاردة مركزية ظاهرية كبيرة تدفع الماء خارج الملابس عبر ثقوب الحوض، مما يؤدي إلى تجفيفها. تزداد كفاءة العصر كلما زادت السرعة الزاوية، ولكن يجب أن يكون تصميم الغسالة قوياً بما يكفي لتحمل الاهتزازات والقوى الناتجة.
• المراوح الكهربائية: تعمل بمبدأ الحركة الدائرية المنتظمة للشفرات حول محور المحرك، حيث تنتج حركة الهواء من الضغط المنخفض خلف الشفرات والضغط المرتفع أمامها. تختلف السرعة الخطية على طول الشفرة من المركز إلى الطرف، مما يؤثر على توزيع حركة الهواء.
• أجهزة الطرد المركزي المنزلية: مثل عصارات الفواكه التي تستخدم الحركة الدائرية عالية السرعة لفصل العصير عن اللب، حيث تكون القوة الطاردة المركزية الظاهرية على الأجزاء الأكثر كثافة أكبر، مما يدفعها نحو الخارج.
• المثاقب الكهربائية وأدوات الطحن: تعتمد على الحركة الدائرية السريعة لرأس الثقب أو قرص الطحن، حيث تتحول الطاقة الكهربائية إلى طاقة حركية دورانية تستخدم في تنفيذ المهام المختلفة.
• أفران الميكروويف الدوارة: تستخدم طبقاً دواراً لضمان توزيع موجات الميكروويف بشكل متساوٍ على الطعام، حيث تكون الحركة الدائرية بطيئة ولكنها ضرورية لتسخين متجانس.

الكفاءة والصيانة

فهم الحركة الدائرية في هذه الأجهزة يساعدنا على استخدامها بكفاءة أكبر وتشخيص المشاكل المحتملة. على سبيل المثال، الاهتزازات غير الطبيعية في الغسالة قد تشير إلى عدم توازن في توزيع الملابس، مما يؤدي إلى حركة دائرية غير منتظمة. كما أن الضجيج غير الطبيعي في المراوح قد يدل على مشاكل في المحامل التي تدعم الحركة الدائرية للشفرات. هذه الأجهزة المنزلية تمثل تطبيقات عملية يومية تجعل مفهوم الحركة الدائرية ملموساً وقابلاً للملاحظة المباشرة، مما يعزز فهمنا لهذه الظاهرة الفيزيائية المهمة.

دور الحركة الدائرية في الصناعة والتصنيع

تشكل الحركة الدائرية العمود الفقري للعديد من العمليات الصناعية الحديثة، حيث تعتمد عليها خطوط الإنتاج والآلات المختلفة في تحويل المواد الخام إلى منتجات نهائية. المحركات الدوارة التي تستخدم في المصانع تحول الطاقة الكهربائية إلى حركة دائرية ميكانيكية يمكن استخدامها في تشغيل الآلات المختلفة. هذه المحركات تتنوع من محركات صغيرة تدير أجهزة بسيطة إلى محركات صناعية ضخمة قادرة على توليد عزوم دوران هائلة لتشغيل المعدات الثقيلة.

في صناعة المعادن، تستخدم المخارط والآلات الدوارة مبادئ الحركة الدائرية لتشكيل المعادن بدقة عالية. تدور قطعة العمل بسرعة زاوية محددة بينما تتحرك أداة القطع بشكل متحكم فيه لإزالة المعدن الزائد وتشكيل القطعة حسب المواصفات المطلوبة. السرعة الزاوية المناسبة والتحكم الدقيق في الحركة الدائرية ضروريان للحصول على منتجات ذات جودة عالية وأبعاد دقيقة. كما تستخدم أجهزة الطرد المركزي الصناعية في فصل المواد ذات الكثافات المختلفة، مثل فصل الزيت عن الماء أو فصل مكونات السوائل المختلفة.

تلعب الحركة الدائرية دوراً حاسماً في صناعة الأسمنت والمواد الخام، حيث تستخدم الأفران الدوارة الضخمة التي تدور ببطء لضمان تسخين متجانس للمواد الخام وتحويلها إلى كلنكر الأسمنت. في صناعة الورق، تستخدم أسطوانات دوارة عديدة لضغط وتجفيف عجينة الورق وتحويلها إلى صفائح ورقية. هذه التطبيقات الصناعية المتنوعة توضح كيف أن فهم الحركة الدائرية ليس مجرد معرفة نظرية، بل هو أساس للعديد من العمليات الصناعية التي تشكل الاقتصاد الحديث. يمكن دراسة هذا التأثير من خلال تحليل التداخلات الاقتصادية بين القطاعات الصناعية المختلفة.

الحركة الدائرية في الظواهر الطبيعية والفلكية

يزخر الكون من حولنا بأمثلة رائعة على الحركة الدائرية الطبيعية، بدءاً من المستوى الذري وصولاً إلى المجرات الضخمة. على المستوى الكوكبي، تدور الأرض حول الشمس في مسار شبه دائري (بيضاوي تقريباً) يكتمل كل 365.25 يوم، وهذه الحركة الدائرية ناتجة عن التوازن بين قوة الجاذبية التي تجذب الأرض نحو الشمس والسرعة المدارية للأرض. لو لم تكن للأرض سرعة مدارية، لسقطت مباشرة نحو الشمس، ولو كانت سرعتها أكبر من اللازم، لانطلقت بعيداً في الفضاء.

تدور الأرض أيضاً حول محورها بحركة دائرية منتظمة تكتمل كل 24 ساعة تقريباً، وهذه الحركة مسؤولة عن تعاقب الليل والنهار. النقاط على خط الاستواء لها سرعة خطية أكبر من النقاط القريبة من القطبين لأنها أبعد عن محور الدوران، ولكن جميع النقاط على سطح الأرض لها نفس السرعة الزاوية. هذا الاختلاف في السرعة الخطية يؤثر على العديد من الظواهر الطبيعية مثل حركة الرياح والتيارات البحرية.

في الغلاف الجوي، تظهر الحركة الدائرية في شكل الأعاصير والأعاصير الحلزونية، حيث تدور كتل الهواء حول مركز ضغط منخفض. هذه الحركة الدائرية ليست عشوائية، بل تخضع لقوانين فيزيائية دقيقة تتعلق بقوة كوريوليس الناتجة عن دوران الأرض. في نصف الكرة الشمالي، تدور الأعاصير عكس عقارب الساعة، بينما تدور في اتجاه عقارب الساعة في نصف الكرة الجنوبي. فهم الحركة الدائرية في هذه الظواهر الجوية يساعد علماء الأرصاد الجوية على التنبؤ بحركة العواصف وشدتها. يمكن الاستفادة من الأبحاث العلمية المصرية في هذا المجال لفهم الظواهر الجوية الإقليمية.

تطبيقات الحركة الدائرية في الفضاء والأقمار الصناعية

تمثل الحركة الدائرية أساس علم الديناميكا المدارية الذي يحكم حركة الأقمار الصناعية والمركبات الفضائية حول الأرض وحول الأجرام السماوية الأخرى. عندما يتم إطلاق قمر صناعي إلى الفضاء، يجب إيصاله إلى سرعة مدارية محددة تعتمد على ارتفاع المدار المطلوب. هذه السرعة المدارية هي بالضبط ما يحتاجه القمر الصناعي للبقاء في حركة دائرية حول الأرض دون أن يسقط أو يهرب إلى الفضاء الخارجي.

تختلف السرعة المدارية المطلوبة باختلاف ارتفاع المدار، فالأقمار الصناعية في المدارات المنخفضة (حوالي 300-500 كيلومتر فوق سطح الأرض) تحتاج إلى سرعات أعلى من الأقمار في المدارات المرتفعة. الأقمار الصناعية الجغرافية الثابتة، التي تبدو وكأنها ثابتة في السماء بالنسبة لنقطة معينة على سطح الأرض، تدور في الواقع حول الأرض بنفس السرعة الزاوية لدوران الأرض حول محورها، وهذا يتطلب وضعها في مدار محدد جداً على ارتفاع حوالي 36,000 كيلومتر فوق خط الاستواء.

المحطة الفضائية الدولية تمثل مثالاً ممتازاً على تطبيق الحركة الدائرية في الفضاء، حيث تدور حول الأرض على ارتفاع حوالي 400 كيلومتر بسرعة تقارب 28,000 كيلومتر في الساعة، مما يجعلها تكمل دورة كاملة حول الأرض كل 90 دقيقة تقريباً. رواد الفضاء داخل المحطة يشعرون بانعدام الوزن ليس لأن الجاذبية معدومة (فالجاذبية عند هذا الارتفاع لا تزال حوالي 90% من قيمتها على السطح)، بل لأنهم والمحطة يسقطون معاً نحو الأرض بنفس التسارع بينما يتحركون أفقياً بسرعة كافية للبقاء في مدار دائري. هذه التطبيقات الفضائية للحركة الدائرية تتطلب حسابات دقيقة للغاية ومعرفة عميقة بالفيزياء المدارية، ويمكن دراسة تأثيرها على القيم الذاتية في معادلات الحركة المدارية.

الحركة الدائرية في الرياضات المختلفة

تطبيقات الحركة الدائرية في الألعاب الرياضية

تظهر الحركة الدائرية بوضوح في العديد من الألعاب الرياضية، حيث يعتمد الأداء الرياضي الناجح على فهم وتطبيق مبادئ هذه الحركة بشكل صحيح:

• رمي المطرقة والقرص: يستخدم الرياضيون الحركة الدائرية لزيادة سرعة الأداة قبل إطلاقها، حيث يدورون عدة دورات كاملة لبناء الزخم الزاوي. كلما زادت السرعة الزاوية ونصف قطر الدوران، زادت السرعة الخطية التي تنطلق بها الأداة عند الإفلات، مما يؤدي إلى مسافة رمي أطول.
• الجمباز والتزلج الفني: يستخدم الرياضيون مبدأ حفظ الزخم الزاوي، حيث يمكنهم زيادة سرعة دورانهم في الهواء عن طريق سحب أطرافهم نحو الجسم، وهذا يقلل من نصف قطر الدوران فتزداد السرعة الزاوية للحفاظ على الزخم الزاوي ثابتاً.
• سباق الدراجات في المضمار: تصمم مضامير السباق بحيث تكون مائلة في المنعطفات، مما يساعد الدراجين على الحفاظ على سرعات عالية في الحركة الدائرية دون الانزلاق. زاوية الميل المثلى تعتمد على نصف قطر المنعطف والسرعة المتوقعة.
• كرة القدم والتنس: عند تنفيذ ركلة أو ضربة منحنية، يطبق اللاعب دوراناً على الكرة، وهذا الدوران (الذي هو شكل من الحركة الدائرية للكرة حول محورها) يتفاعل مع الهواء ليولد قوة جانبية تجعل الكرة تنحني في مسارها.
• السباحة: في منعطفات حمامات السباحة، يستخدم السباحون تقنيات خاصة للدوران تعتمد على مبادئ الحركة الدائرية لتقليل الزمن المستغرق في تغيير الاتجاه.

التدريب والأداء الرياضي

فهم مبادئ الحركة الدائرية يساعد المدربين والرياضيين على تحسين الأداء وتجنب الإصابات. عند تنفيذ حركات دورانية سريعة، يجب على الرياضي أن يكون واعياً للقوى التي تؤثر على جسمه، خاصة القوة الطاردة المركزية الظاهرية التي قد تسبب فقدان التوازن إذا لم يتم التعامل معها بشكل صحيح. كما أن فهم العلاقة بين السرعة الزاوية ونصف القطر يساعد الرياضيين على تحسين تقنياتهم في الألعاب التي تتطلب دوراناً. هذه التطبيقات الرياضية للحركة الدائرية تجعل المفهوم الفيزيائي ملموساً ومرئياً، مما يساعد على فهم أفضل لهذه الظاهرة.

أهمية الحركة الدائرية في الهندسة الميكانيكية

تعد الحركة الدائرية من المفاهيم الأساسية التي يجب على كل مهندس ميكانيكي إتقانها، حيث تدخل في تصميم معظم الآلات والأنظمة الميكانيكية. تستخدم التروس والبكرات وأحزمة النقل مبادئ الحركة الدائرية لنقل القوة والحركة من مكان إلى آخر في الآلة. العلاقة بين سرعات الدوران وأنصاف الأقطار في أنظمة التروس المترابطة تحكمها قوانين الحركة الدائرية، حيث يمكن زيادة أو تقليل السرعة الزاوية مع تغيير عزم الدوران وفقاً لمبدأ حفظ الطاقة.

في تصميم المحركات الدوارة، سواء كانت محركات احتراق داخلي أو محركات كهربائية، يجب على المهندسين حساب القوى والعزوم المرتبطة بالحركة الدائرية بدقة عالية. التوازن الديناميكي للأجزاء الدوارة ضروري لتقليل الاهتزازات والضجيج وضمان عمر أطول للآلة. أي عدم توازن في الأجزاء الدوارة يؤدي إلى قوى طاردة مركزية غير متوازنة تسبب اهتزازات يمكن أن تكون مدمرة عند السرعات العالية. لذلك، يتم إجراء عمليات موازنة دقيقة للعديد من المكونات الدوارة مثل عمود المرفق في المحركات وشفرات التوربينات.

في مجال الروبوتات والأتمتة الصناعية، تستخدم المفاصل الدوارة والمحركات الخطوية التي تعتمد على الحركة الدائرية لتحقيق حركات دقيقة ومتحكم فيها. فهم ديناميكيات الحركة الدائرية يساعد في برمجة هذه الروبوتات لتنفيذ مهام معقدة بدقة وسرعة عاليتين. كما تستخدم أنظمة التعليق في المركبات مبادئ الحركة الدائرية في امتصاص الصدمات، حيث تتحول الحركة الخطية الناتجة عن المطبات على الطريق إلى حركة دائرية في ماصات الصدمات الدوارة. تتطلب هذه التطبيقات الهندسية معرفة شاملة بالحركة الدائرية وتطبيقاتها، ويمكن الاستفادة من علوم الصرف في فهم تدفق السوائل في الأنظمة الدوارة.

الحركة الدائرية في الأنظمة البيولوجية والطبيعية

على الرغم من أن الطبيعة الحية لا تحتوي على عجلات بالمعنى الميكانيكي التقليدي، إلا أن الحركة الدائرية تظهر في العديد من الأنظمة البيولوجية بطرق مبتكرة. البكتيريا التي تتحرك بواسطة السوط (Flagellum) تستخدم محركاً بيولوجياً دواراً يعد من أصغر المحركات الدوارة المعروفة في الطبيعة. هذا المحرك البكتيري يدور بسرعات تصل إلى مئات الدورات في الثانية، مولداً حركة دائرية للسوط ينتج عنها دفع البكتيريا في السائل المحيط بها.

في جسم الإنسان، نجد أمثلة على الحركة الدائرية في المفاصل الكروية مثل مفصل الكتف والورك، حيث تسمح هذه المفاصل بحركة دائرية واسعة النطاق للذراع والساق. حركة الدم في الأوعية الدموية الدوامة (Vortex Flow) تمثل شكلاً من الحركة الدائرية التي تساعد على خلط الدم وضمان توزيع الأكسجين والمواد الغذائية بشكل متجانس. كما أن دوران العين لتتبع الأجسام المتحركة يعتمد على حركة دائرية دقيقة للعضلات المحيطة بالعين.

في عالم النبات، نجد ظاهرة اللف الحلزوني (Circumnutation) حيث تنمو بعض النباتات المتسلقة بحركة دائرية حلزونية حول دعامة للالتفاف عليها والصعود إلى الأعلى. هذه الحركة الدائرية البطيئة والمستمرة تمكن النبات من العثور على الدعامة والالتفاف حولها بإحكام. هذه الأمثلة البيولوجية توضح أن الحركة الدائرية ليست مجرد ظاهرة فيزيائية في الآلات والأنظمة الميكانيكية، بل هي أيضاً استراتيجية إستراتيجية تطورت في النظم الحية لتحقيق وظائف حيوية مختلفة. يمكن دراسة هذه الظواهر من خلال الموسيقى السورية التي تحتوي على أنماط دائرية متكررة في الإيقاع.

الحركة الدائرية وتطبيقاتها في توليد الطاقة

تعتمد معظم محطات توليد الطاقة الكهربائية على مبدأ تحويل أشكال مختلفة من الطاقة إلى حركة دائرية ثم إلى طاقة كهربائية. في محطات الطاقة الحرارية، سواء كانت تعمل بالفحم أو الغاز الطبيعي أو الطاقة النووية، يتم تسخين الماء لإنتاج بخار عالي الضغط يدفع شفرات التوربين في حركة دائرية عالية السرعة. هذه الحركة الدائرية للتوربين تنقل إلى المولد الكهربائي الذي يحول الطاقة الميكانيكية الدورانية إلى طاقة كهربائية من خلال الحث الكهرومغناطيسي.

في محطات الطاقة الكهرومائية، تستخدم طاقة المياه المتساقطة لتدوير التوربينات في حركة دائرية. قوة الماء المندفع توفر العزم اللازم لتدوير التوربين، والسرعة الزاوية للتوربين تعتمد على معدل تدفق الماء وارتفاع السقوط. كفاءة هذه المحطات تعتمد بشكل كبير على تصميم شفرات التوربين وفهم ديناميكيات الحركة الدائرية للسوائل. مزارع طاقة الرياح تمثل مثالاً آخر على استخدام الحركة الدائرية في توليد الطاقة، حيث تدفع الرياح شفرات التوربينات الهوائية الضخمة في حركة دائرية، وهذه الحركة تنقل عبر صندوق تروس إلى المولد الكهربائي.

حتى في محركات السيارات، يتم تحويل الطاقة الكيميائية في الوقود إلى حركة خطية للمكابس، ثم تحول هذه الحركة الخطية إلى حركة دائرية لعمود المرفق الذي ينقل الحركة إلى العجلات. فهم الحركة الدائرية في هذه الأنظمة يساعد على تحسين كفاءة تحويل الطاقة وتقليل الفاقد. جميع هذه التطبيقات توضح أن الحركة الدائرية هي الوسيط الرئيس لتحويل أشكال الطاقة المختلفة إلى طاقة كهربائية مفيدة، مما يجعلها حجر الأساس في البنية التحتية للطاقة الحديثة. يمكن تحليل هذه الأنظمة باستخدام القنوات والصرف لفهم تدفق السوائل في المحطات الكهرومائية.

الحساسات والأجهزة القياسية المعتمدة على الحركة الدائرية

تستخدم العديد من أجهزة القياس والحساسات الحديثة مبادئ الحركة الدائرية للكشف عن الحركة والسرعة والتسارع والدوران. الجيروسكوب (Gyroscope) هو أحد أهم هذه الأجهزة، حيث يستخدم حركة دائرية عالية السرعة لقرص أو عجلة دوارة للحفاظ على اتجاه ثابت في الفضاء. يعتمد الجيروسكوب على مبدأ حفظ الزخم الزاوي، حيث يقاوم أي محاولة لتغيير محور دورانه، مما يجعله مفيداً جداً في أنظمة الملاحة والتوجيه في الطائرات والسفن والصواريخ.

العدادات الدوارة (Rotary Encoders) تستخدم الحركة الدائرية لقياس الموضع الزاوي أو السرعة الزاوية بدقة عالية. هذه الأجهزة تحول الحركة الدائرية الميكانيكية إلى إشارات كهربائية رقمية يمكن للحاسوب قراءتها ومعالجتها. تستخدم العدادات الدوارة على نطاق واسع في الروبوتات والآلات الصناعية والطابعات ثلاثية الأبعاد لضمان الحركة الدقيقة والمتحكم فيها. مقاييس التسارع الدورانية (Rotational Accelerometers) تكشف التسارعات الزاوية في الأنظمة الدوارة، وهي ضرورية في العديد من التطبيقات مثل أنظمة التحكم في استقرار المركبات.

في عالم الإلكترونيات الاستهلاكية، تستخدم الهواتف الذكية والأجهزة اللوحية جيروسكوبات دقيقة للكشف عن دوران الجهاز وتوجيهه، مما يمكن الجهاز من تدوير الشاشة تلقائياً أو تحسين دقة تحديد الموقع في تطبيقات الخرائط والملاحة. هذه الحساسات المصغرة تعتمد على مبادئ الحركة الدائرية ولكن بحجم صغير جداً لا يتجاوز بضعة ملليمترات. فهم الحركة الدائرية في هذه الأجهزة الحساسة يتطلب معرفة متقدمة بالفيزياء والهندسة الدقيقة.

التحديات الهندسية المرتبطة بالحركة الدائرية عالية السرعة

عندما تصل سرعات الحركة الدائرية إلى قيم عالية جداً، تظهر تحديات هندسية فريدة يجب التعامل معها بعناية. القوى الطاردة المركزية الناتجة عن الحركة الدائرية عالية السرعة يمكن أن تكون هائلة، مما يضع ضغطاً ميكانيكياً كبيراً على المواد. في التوربينات الغازية المستخدمة في محركات الطائرات النفاثة، تدور الشفرات بسرعات زاوية عالية جداً وتتعرض لدرجات حرارة مرتفعة وقوى طاردة مركزية ضخمة، مما يتطلب استخدام سبائك معدنية خاصة ذات قوة عالية ومقاومة للحرارة.

مشكلة الرنين (Resonance) تمثل تحدياً خطيراً في الأنظمة الدوارة عالية السرعة. كل نظام ميكانيكي له ترددات طبيعية يهتز عندها بسهولة، وإذا تزامنت سرعة الدوران مع أحد هذه الترددات الطبيعية، يمكن أن تحدث اهتزازات عنيفة قد تؤدي إلى فشل كارثي في النظام. لذلك، يجب على المهندسين تصميم الأنظمة الدوارة بحيث تعمل بسرعات بعيدة عن الترددات الطبيعية، أو استخدام أجهزة تخميد لامتصاص الاهتزازات.

التآكل والاحتكاك في المحامل التي تدعم الأجزاء الدوارة يزداد مع زيادة السرعة، مما يتطلب استخدام تقنيات تشحيم متقدمة أو محامل مغناطيسية أو هوائية تقلل الاحتكاك المباشر. في أجهزة الطرد المركزي الفائقة السرعة المستخدمة في الأبحاث العلمية، يتم تشغيل الدوار في فراغ لتقليل مقاومة الهواء، وتستخدم محامل مغناطيسية للحفاظ على الدوار معلقاً دون احتكاك مباشر. هذه التحديات الهندسية تتطلب فهماً عميقاً للحركة الدائرية وتفاعلها مع المواد والبيئة المحيطة، وتمثل مجالاً نشطاً للبحث والتطوير في الهندسة الميكانيكية وعلوم المواد.

الحركة الدائرية في الساعات وأجهزة قياس الوقت

تمثل الساعات أحد أقدم وأشهر التطبيقات العملية للحركة الدائرية المنتظمة في حياة الإنسان. منذ اختراع الساعات الميكانيكية قبل قرون، اعتمدت هذه الأجهزة على حركة دائرية دقيقة ومنتظمة للعقارب لقياس الوقت بدقة. في الساعات الميكانيكية التقليدية، تستخدم بندولة أو نابض توازن لتنظيم الحركة الدائرية لمجموعة من التروس المتشابكة التي تنقل الحركة إلى عقارب الساعة بسرعات زاوية محددة بدقة.

عقرب الثواني يكمل دورة كاملة كل 60 ثانية، وعقرب الدقائق يكمل دورة كاملة كل 60 دقيقة، بينما عقرب الساعات يكمل دورة كاملة كل 12 ساعة. هذه السرعات الزاوية المختلفة تتحقق من خلال نظام تروس دقيق يحول الحركة الدائرية الأساسية إلى سرعات دورانية مختلفة للعقارب. الدقة في صناعة الساعات تتطلب فهماً عميقاً للحركة الدائرية والاحتكاك والتآكل، حيث أن أي خطأ صغير في السرعة الزاوية يتراكم مع الوقت ويؤدي إلى عدم دقة في قياس الوقت.

في العصر الحديث، تستخدم الساعات الرقمية بلورات الكوارتز التي تهتز بتردد منتظم للغاية لقياس الوقت، ولكن حتى هذه الساعات غالباً ما تعرض الوقت بواسطة عقارب دوارة في حركة دائرية لأن هذا الشكل من العرض مألوف وسهل القراءة. الساعات الذرية، التي تعد أدق أجهزة قياس الوقت المعروفة، تستخدم تذبذبات الذرات لقياس الوقت، ولكن لعرض الوقت بطريقة مفيدة، يتم تحويل هذه التذبذبات إلى حركة دائرية للعقارب أو أرقام رقمية. هذا التطور التاريخي في تقنيات قياس الوقت يوضح كيف ظلت الحركة الدائرية مفهوماً مركزياً عبر العصور، من الساعات الميكانيكية البسيطة إلى الساعات الذرية فائقة الدقة.

الحركة الدائرية في عالم المجهريات والنانو

على المستوى المجهري والنانوي، تظهر الحركة الدائرية في أشكال مثيرة للاهتمام ومبتكرة. المحركات الجزيئية (Molecular Motors) الموجودة في الخلايا الحية، مثل ATP Synthase الذي ينتج جزيئات الطاقة ATP، تعمل بمبدأ الحركة الدائرية على المستوى الجزيئي. هذا الإنزيم يحتوي على جزء دوار يدور بسرعة عالية جداً (حوالي 100 دورة في الثانية) مدفوعاً بتدفق أيونات الهيدروجين عبر غشاء الخلية، وهذه الحركة الدائرية تستخدم لتصنيع ATP.

في مجال النانوتكنولوجي، يعمل العلماء على تطوير آلات نانوية دوارة يمكن استخدامها في تطبيقات متنوعة مثل توصيل الأدوية داخل الجسم أو بناء هياكل نانوية معقدة. هذه الآلات النانوية تواجه تحديات فريدة لا تواجهها الآلات الدوارة الكبيرة، مثل تأثير الحركة البراونية العشوائية والقوى الجزيئية التي تصبح مهيمنة على هذا المقياس. فهم الحركة الدائرية على المستوى النانوي يتطلب دمج الفيزياء الكلاسيكية مع ميكانيكا الكم والديناميكا الحرارية الإحصائية.

المجاهر الدوارة (Spinning Disk Microscopes) تستخدم قرصاً دواراً بسرعة عالية يحتوي على فتحات دقيقة لتحسين جودة التصوير في المجهر الضوئي. الحركة الدائرية السريعة للقرص تسمح بمسح العينة بسرعة عالية والحصول على صور ثلاثية الأبعاد بدقة عالية. في أجهزة الطرد المركزي النانوية، تستخدم سرعات دوران فائقة لفصل وتحليل الجسيمات النانوية والجزيئات الكبيرة. هذه التطبيقات المجهرية للحركة الدائرية تفتح آفاقاً جديدة في البحث العلمي والطب والتكنولوجيا، وتوضح أن مبادئ الحركة الدائرية تبقى صالحة ومفيدة عبر نطاق واسع من المقاييس، من المجرات الضخمة إلى الجزيئات المجهرية.

الحركة الدائرية والتحكم الآلي والأتمتة

في عصر الأتمتة والتصنيع الذكي، تلعب الحركة الدائرية دوراً محورياً في أنظمة التحكم الآلي. المحركات الخطوية (Stepper Motors) والمحركات المؤازرة (Servo Motors) التي تستخدم على نطاق واسع في الروبوتات والآلات الصناعية توفر تحكماً دقيقاً في الحركة الدائرية. هذه المحركات يمكنها التحرك بزوايا محددة بدقة عالية جداً، مما يجعلها مثالية للتطبيقات التي تتطلب وضعاً دقيقاً.

في خطوط الإنتاج الأوتوماتيكية، تستخدم أنظمة الناقلات الدوارة لنقل المنتجات بين مراحل التصنيع المختلفة. هذه الأنظمة تعتمد على حركة دائرية منتظمة لضمان تدفق سلس ومنظم للمنتجات. السرعة الزاوية للناقلات يمكن التحكم فيها بدقة لتتناسب مع سرعة عمليات التصنيع المختلفة، مما يحسن الكفاءة الإجمالية لخط الإنتاج. في أنظمة الرؤية الآلية للفحص الجودة، تستخدم كاميرات دوارة أو أجسام دوارة لفحص المنتجات من جميع الجوانب باستخدام الحركة الدائرية.

أنظمة التحكم في الحركة (Motion Control Systems) الحديثة تستخدم خوارزميات متقدمة لحساب السرعات الزاوية والتسارعات المطلوبة لتحقيق حركة دائرية سلسة ودقيقة. هذه الأنظمة تأخذ في الاعتبار القصور الذاتي للأجزاء الدوارة، والاحتكاك، والقوى الخارجية لضمان حركة مثالية. في الطابعات ثلاثية الأبعاد، تستخدم محركات خطوية لتحريك رأس الطباعة في مسارات دقيقة، والعديد من هذه المسارات تتضمن أقواساً دائرية تتطلب حساباً دقيقاً للحركة الدائرية. فهم الحركة الدائرية وتطبيقها في أنظمة التحكم الآلي يمكن دراسته من خلال علوم المصارف لفهم تدفق الموارد في الأنظمة الصناعية.

خاتمة

تمثل الحركة الدائرية أحد أهم المفاهيم الفيزيائية التي تتخلل حياتنا اليومية بطرق لا حصر لها. من دوران الأرض حول الشمس إلى حركة عقارب الساعة، ومن المحركات في السيارات إلى التوربينات في محطات الطاقة، تظهر الحركة الدائرية كمبدأ أساسي يحكم العديد من الظواهر الطبيعية والتطبيقات التكنولوجية. فهم القوانين الفيزيائية التي تحكم الحركة الدائرية، مثل القوة المركزية والتسارع المركزي والعلاقة بين السرعة الخطية والسرعة الزاوية، يفتح أمامنا آفاقاً واسعة لاستيعاب آليات عمل الكون من حولنا.

إن دراسة الحركة الدائرية لا تقتصر على الجانب النظري فحسب، بل تمتد لتشمل تطبيقات عملية لا حصر لها في مختلف المجالات. في الهندسة الميكانيكية، توفر مبادئ الحركة الدائرية الأساس لتصميم الآلات والمحركات الفعالة. في الفضاء، تحكم هذه المبادئ حركة الأقمار الصناعية والمركبات الفضائية. في الطب والبيولوجيا، نجد الحركة الدائرية في أصغر المحركات الجزيئية داخل خلايانا. في الترفيه، توفر لنا ألعاب المدن الترفيهية تجارب مثيرة تعتمد على هذا المبدأ الفيزيائي. كل هذه التطبيقات المتنوعة تؤكد على الطبيعة العالمية والشمولية للحركة الدائرية كظاهرة فيزيائية أساسية.

مع استمرار التقدم العلمي والتكنولوجي، يبقى فهم الحركة الدائرية ضرورياً للمهندسين والعلماء والمبتكرين الذين يعملون على تطوير تقنيات جديدة ومحسنة. من تطوير توربينات رياح أكثر كفاءة لتوليد الطاقة النظيفة، إلى تصميم آلات نانوية دوارة لتطبيقات طبية متقدمة، تظل الحركة الدائرية في قلب الابتكار التكنولوجي. إن القدرة على تحليل وفهم الحركة الدائرية بعمق ليست مجرد مهارة أكاديمية، بل هي أداة عملية قوية تمكننا من تحسين حياتنا اليومية وتطوير حلول مبتكرة للتحديات التي نواجهها في العالم الحديث.

الأسئلة الشائعة

1. ما هو الفرق بين الحركة الدائرية المنتظمة وغير المنتظمة؟

الحركة الدائرية المنتظمة هي تلك التي يتحرك فيها الجسم بسرعة خطية ثابتة المقدار على طول محيط الدائرة، بينما تتغير سرعته الاتجاهية باستمرار. في هذا النوع، تكون السرعة الزاوية ثابتة والتسارع مركزياً فقط موجهاً نحو المركز. أما الحركة الدائرية غير المنتظمة فهي تلك التي تتغير فيها السرعة الخطية أو السرعة الزاوية للجسم أثناء حركته على المسار الدائري، مما يؤدي إلى وجود تسارع مركزي يغير اتجاه السرعة وتسارع مماسي يغير مقدارها.

2. لماذا تحتاج الأجسام في الحركة الدائرية إلى قوة مركزية مستمرة؟

تحتاج الأجسام في الحركة الدائرية إلى قوة مركزية مستمرة بسبب قانون نيوتن الأول للحركة الذي ينص على أن الجسم يميل للاستمرار في خط مستقيم بسرعة ثابتة ما لم تؤثر عليه قوة خارجية. لأن المسار الدائري يتطلب تغييراً مستمراً في اتجاه السرعة، فإن هذا التغيير في الاتجاه يمثل تسارعاً يحتاج إلى قوة لإحداثه. هذه القوة المركزية تعمل على ثني مسار الجسم باستمرار نحو المركز، مانعة إياه من الانطلاق في خط مستقيم والحفاظ عليه في مساره الدائري.

3. كيف تختلف السرعة الخطية عن السرعة الزاوية في الحركة الدائرية؟

السرعة الخطية تقيس المسافة الفعلية التي يقطعها الجسم على محيط الدائرة في وحدة الزمن وتقاس بوحدة متر/ثانية، وهي متجهة في اتجاه مماس للدائرة عند كل نقطة. أما السرعة الزاوية فتقيس معدل تغير الموضع الزاوي بالنسبة للزمن وتقاس بوحدة راديان/ثانية أو درجة/ثانية. العلاقة بينهما تعطى بالمعادلة v = ωr، حيث تزداد السرعة الخطية كلما ابتعدنا عن المركز عند ثبات السرعة الزاوية، بينما تبقى السرعة الزاوية نفسها لجميع نقاط الجسم الصلب الدوار.

4. ما هي القوة الطاردة المركزية وهل هي قوة حقيقية؟

القوة الطاردة المركزية ليست قوة حقيقية بالمعنى الفيزيائي، بل هي قوة ظاهرية أو وهمية تنشأ من منظور مراقب يتحرك في إطار مرجعي دوار. عندما نكون داخل نظام دوار، نشعر بقوة تدفعنا نحو الخارج بسبب ميل أجسامنا للاستمرار في خط مستقيم وفقاً لقانون القصور الذاتي. القوة الحقيقية الوحيدة المؤثرة هي القوة المركزية التي تجذب الجسم نحو المركز، ولكن من وجهة نظر المراقب الدوار، تظهر قوة طاردة ظاهرية توازن القوة المركزية في حالة الحركة الدائرية المنتظمة.

5. كيف يؤثر نصف قطر المسار الدائري على القوة المركزية المطلوبة؟

نصف قطر المسار الدائري له تأثير عكسي على القوة المركزية المطلوبة، حيث تتناسب القوة المركزية عكسياً مع نصف القطر وفقاً للمعادلة F = mv²/r. هذا يعني أنه عند ثبات السرعة الخطية والكتلة، كلما قل نصف قطر المسار الدائري، زادت القوة المركزية المطلوبة للحفاظ على الجسم في هذا المسار. لهذا السبب، تكون المنعطفات الحادة ذات نصف القطر الصغير أكثر خطورة للسيارات المتحركة بسرعة عالية، حيث قد لا تكون قوة الاحتكاك كافية لتوفير القوة المركزية الكبيرة المطلوبة.

6. ما هو التسارع المركزي ولماذا يوجد حتى في الحركة الدائرية المنتظمة؟

التسارع المركزي هو التسارع الموجه دائماً نحو مركز الدائرة والمسؤول عن تغيير اتجاه السرعة في الحركة الدائرية. يحسب بالمعادلة a = v²/r أو a = ω²r. حتى في الحركة الدائرية المنتظمة حيث يبقى مقدار السرعة ثابتاً، يوجد تسارع مركزي لأن التسارع يعرف بأنه معدل تغير السرعة المتجهة مع الزمن، والسرعة المتجهة تشمل كلاً من المقدار والاتجاه. بما أن اتجاه السرعة يتغير باستمرار في الحركة الدائرية، فإن ذلك يمثل تسارعاً حتى لو ظل مقدار السرعة ثابتاً.

7. كيف تستخدم الحركة الدائرية في فصل المواد في أجهزة الطرد المركزي؟

تستخدم أجهزة الطرد المركزي الحركة الدائرية عالية السرعة لتوليد قوى طاردة مركزية ظاهرية كبيرة جداً، أكبر بكثير من قوة الجاذبية الأرضية. عندما يدور الجهاز بسرعة عالية، تتعرض المواد ذات الكثافات المختلفة لقوى طاردة مركزية مختلفة تتناسب مع كتلتها وبعدها عن المركز. المواد الأكثر كثافة تتحرك نحو الخارج بشكل أسرع من المواد الأقل كثافة، مما يؤدي إلى فصل المكونات المختلفة في طبقات متمايزة. هذه التقنية تستخدم على نطاق واسع في المختبرات الطبية لفصل مكونات الدم وفي الصناعة لفصل السوائل عن المواد الصلبة.

8. ما العلاقة بين الحركة الدائرية وقانون حفظ الزخم الزاوي؟

قانون حفظ الزخم الزاوي ينص على أن الزخم الزاوي لنظام معزول يبقى ثابتاً في غياب عزوم خارجية. الزخم الزاوي يحسب بالمعادلة L = Iω حيث I هو عزم القصور الذاتي و ω هي السرعة الزاوية. في الحركة الدائرية، عندما يتغير نصف قطر الدوران ويقل عزم القصور الذاتي، يجب أن تزداد السرعة الزاوية للحفاظ على الزخم الزاوي ثابتاً. هذا المبدأ يفسر لماذا يدور المتزلج على الجليد بسرعة أكبر عندما يسحب ذراعيه نحو جسده، ولماذا تدور الكواكب بسرعة أكبر عندما تقترب من الشمس في مداراتها البيضاوية.

9. كيف يتم حساب الفترة الزمنية والتردد في الحركة الدائرية المنتظمة؟

الفترة الزمنية في الحركة الدائرية المنتظمة هي الوقت اللازم لإكمال دورة كاملة واحدة، وتحسب بالمعادلة T = 2πr/v أو T = 2π/ω، حيث r هو نصف القطر، v هي السرعة الخطية، و ω هي السرعة الزاوية. أما التردد فهو عدد الدورات الكاملة في وحدة الزمن ويحسب بالمعادلة f = 1/T، ويقاس بوحدة هرتز التي تساوي دورة واحدة في الثانية. العلاقة بين التردد والسرعة الزاوية تعطى بـ ω = 2πf. هذه العلاقات الرياضية أساسية لفهم وتحليل الحركة الدائرية المنتظمة في مختلف التطبيقات العملية.

10. ما الدور الذي تلعبه إمالة الطرق في المنعطفات الدائرية؟

إمالة الطرق في المنعطفات الدائرية تساعد في توفير جزء من القوة المركزية المطلوبة من خلال مكون الوزن الموجه نحو مركز المنعطف. عندما يكون الطريق مائلاً بزاوية مناسبة، ينتج عن وزن المركبة مكون أفقي موجه نحو المركز يساهم في القوة المركزية، مما يقلل الاعتماد الكلي على قوة الاحتكاك وحدها. زاوية الإمالة المثلى تحسب بناءً على نصف قطر المنعطف والسرعة المصممة للطريق باستخدام المعادلة tan(θ) = v²/(rg). هذا التصميم الهندسي يحسن أمان المركبات ويسمح بسرعات أعلى في المنعطفات مع تقليل خطر الانزلاق.