مبدأ أرخميدس: من التاج الذهبي إلى أساسيات الطفو وميكانيكا الموائع

المقدمة: حجر الزاوية في ميكانيكا الموائع

يعتبر مبدأ أرخميدس (Archimedes’ Principle) أحد أقدم وأهم القوانين الأساسية في الفيزياء، وتحديداً في فرع ميكانيكا الموائع (Fluid Mechanics). على الرغم من بساطة نصه، إلا أن فهمه العميق يفتح آفاقاً واسعة لتفسير ظواهر طبيعية وهندسية لا حصر لها، بدءاً من طفو السفن العملاقة ووصولاً إلى تحليق المناطيد في السماء. يقوم مبدأ أرخميدس على ملاحظة أساسية مفادها أن أي جسم مغمور كلياً أو جزئياً في مائع (سائل أو غاز) يتعرض لقوة دفع رأسية إلى الأعلى، تُعرف بقوة الطفو (Buoyant Force)، وهذه القوة تساوي في مقدارها وزن المائع الذي يزيحه الجسم. إن هذا القانون الفيزيائي الخالد، الذي يُنسب إلى العالم اليوناني القديم أرخميدس، لا يزال يشكل الركيزة التي تُبنى عليها تصميمات هندسية معقدة وتُفسر بها ظواهر جيولوجية وبيولوجية دقيقة. إن استيعاب مبدأ أرخميدس ليس مجرد تمرين أكاديمي، بل هو ضرورة لفهم كيفية تفاعل الأجسام مع محيطها المائع. تشكل التطبيقات العملية لمبدأ أرخميدس دليلاً قاطعاً على عبقرية هذا الاكتشاف وأثره الممتد عبر القرون. في هذه المقالة، سنستعرض مبدأ أرخميدس من جوانبه التاريخية، وصياغته العلمية والرياضية، والعوامل المؤثرة فيه، وأبرز تطبيقاته في حياتنا اليومية وفي مختلف فروع العلم، مما يوضح لماذا يظل مبدأ أرخميدس مفهوماً محورياً في الفيزياء الحديثة.

السياق التاريخي: قصة “يوريكا!” واكتشاف مبدأ أرخميدس

لا يمكن فصل مبدأ أرخميدس عن قصته التاريخية الشهيرة التي أصبحت جزءاً من التراث العلمي العالمي. تعود القصة إلى القرن الثالث قبل الميلاد في مدينة سيراقوسة (Syracuse)، حيث كُلّف العالم والمخترع العظيم أرخميدس من قبل الملك هيرون الثاني بمهمة تبدو مستحيلة في ذلك الوقت. شك الملك في أن الصائغ الذي صنع له تاجاً جديداً من الذهب الخالص قد غشه وخلط الذهب بالفضة الأقل قيمة. كانت المشكلة تكمن في كيفية التحقق من مكونات التاج دون إتلافه أو صهره. شكلت هذه المعضلة تحدياً فكرياً هائلاً، حيث كان من المعروف أن للذهب كثافة أعلى من الفضة، ولكن قياس حجم جسم غير منتظم الشكل مثل التاج كان أمراً بالغ الصعوبة.

تقول الرواية، التي ذكرها المهندس الروماني فيتروفيوس (Vitruvius) بعد قرون، أن أرخميدس وجد الحل بينما كان يستحم. لاحظ عند دخوله حوض الاستحمام الممتلئ بالماء أن مستوى الماء قد ارتفع، وأن جسده شعر بخفة نسبية. في تلك اللحظة الخاطفة من الإلهام، أدرك أن حجم الماء المزاح يساوي تماماً حجم الجزء المغمور من جسده. هذه الملاحظة البسيطة كانت المفتاح لحل لغز التاج، حيث يمكن قياس حجم أي جسم، مهما كان شكله معقداً، عن طريق قياس حجم الماء الذي يزيحه عند غمره. انطلق أرخميدس من الحمام وهو يركض في شوارع سيراقوسة عارياً ويصيح “يوريكا! يوريكا!” (Eureka! Eureka!)، وهي كلمة يونانية تعني “وجدتها!”. كان هذا الاكتشاف هو النواة التي تشكل منها مبدأ أرخميدس.

لاحقاً، طور أرخميدس هذه الفكرة لتصبح قانوناً علمياً متكاملاً. أدرك أن قوة الدفع التي شعر بها في الماء (الطفو) مرتبطة بالماء المزاح. وهكذا، وُلد مبدأ أرخميدس الذي ينص على أن قوة الطفو تساوي وزن المائع المزاح. بتطبيق هذا المبدأ، تمكن أرخميدس من حل مشكلة التاج بسهولة. قام بغمر التاج في الماء وقاس حجم الماء المزاح، ثم قام بغمر كتلة من الذهب الخالص مساوية لوزن التاج في الماء وقاس حجم الماء المزاح. لو كان التاج مصنوعاً من الذهب الخالص، لكان حجم الماء المزاح في الحالتين متطابقاً. ولكن، وجد أرخميدس أن التاج أزاح كمية أكبر من الماء، مما يعني أن حجمه أكبر من حجم كتلة الذهب المساوية له في الوزن، وهذا بدوره يثبت أن كثافته أقل، أي أنه مخلوط بمعدن أخف مثل الفضة. وهكذا، كُشف أمر الصائغ بفضل مبدأ أرخميدس.

الصياغة العلمية لمبدأ أرخميدس وقوة الطفو

لفهم مبدأ أرخميدس بشكل علمي دقيق، يجب أولاً تعريف المفاهيم الأساسية المرتبطة به. المائع (Fluid) هو أي مادة قابلة للتدفق وليس لها شكل ثابت، وتشمل السوائل والغازات. عندما يُغمر جسم في مائع، فإن المائع يؤثر على جميع أسطح الجسم بقوة ضغط عمودية عليها. قوة الطفو (Buoyant Force)، التي يرمز لها بـ (Fb)، هي محصلة هذه القوى.

ينص مبدأ أرخميدس بشكل رسمي على ما يلي: “الجسم المغمور كلياً أو جزئياً في مائع ساكن، يتأثر بقوة طفو رأسية إلى الأعلى مقدارها يساوي وزن المائع الذي يزيحه الجسم”.

يمكن التعبير عن هذه العلاقة بالصيغة الرياضية التالية:
Fb = ρf * V * g

حيث:

• Fb: هي قوة الطفو (Buoyant Force)، وتُقاس بوحدة نيوتن (N).
• ρf (رو-إف): هي كثافة المائع (Density of the fluid)، وتُقاس بوحدة كيلوجرام لكل متر مكعب (kg/m³).
• V: هو حجم المائع المزاح (Volume of displaced fluid)، والذي يساوي حجم الجزء المغمور من الجسم، ويُقاس بالمتر المكعب (m³).
• g: هو ثابت تسارع الجاذبية الأرضية (Acceleration due to gravity)، وقيمته التقريبية 9.8 متر لكل ثانية مربعة (m/s²).

من المهم ملاحظة أن حاصل ضرب كثافة المائع (ρf) في حجم المائع المزاح (V) يعطينا كتلة المائع المزاح (mf = ρf * V). وعند ضرب هذه الكتلة في تسارع الجاذبية (g)، نحصل على وزن المائع المزاح (Wf = mf * g). إذن، الصيغة الرياضية هي ترجمة مباشرة لنص مبدأ أرخميدس. إن جوهر مبدأ أرخميدس يكمن في هذه العلاقة المباشرة بين قوة الدفع وحجم الجزء المغمور من الجسم وكثافة المائع المحيط. لذلك، فإن أي تغيير في أي من هذين المتغيرين سيؤدي حتماً إلى تغيير في قوة الطفو التي يتعرض لها الجسم. إن الفهم العميق لهذه المعادلة هو مفتاح تحليل جميع الظواهر المتعلقة بالطفو والغوص، وهو ما يجعل مبدأ أرخميدس أداة تحليلية قوية للغاية في يد الفيزيائيين والمهندسين.

الإثبات الرياضي: فهم مبدأ أرخميدس من منظور الضغط

يمكن إثبات مبدأ أرخميدس رياضياً بالاعتماد على مفهوم أساسي في ميكانيكا الموائع، وهو أن الضغط (Pressure) في المائع يزداد مع زيادة العمق. لنفترض وجود جسم على شكل متوازي مستطيلات منتظم، مغمور بالكامل في مائع كثافته (ρf). لنتخيل أن ارتفاع الجسم هو (h) ومساحة قاعدته العلوية والسفلية هي (A).

1. القوة على السطح العلوي: يتعرض السطح العلوي للجسم، الموجود على عمق (d1)، لضغط من المائع مقداره (P1 = ρf * g * d1). وبالتالي، فإن القوة المؤثرة على هذا السطح (F1) تكون رأسية إلى الأسفل ومقدارها:
   F1 = P1 * A = ρf * g * d1 * A
2. القوة على السطح السفلي: يتعرض السطح السفلي للجسم، الموجود على عمق أكبر (d2 = d1 + h)، لضغط مقداره (P2 = ρf * g * d2). وبالتالي، فإن القوة المؤثرة على هذا السطح (F2) تكون رأسية إلى الأعلى ومقدارها:
   F2 = P2 * A = ρf * g * d2 * A = ρf * g * (d1 + h) * A
3. القوى على الجوانب: القوى المؤثرة على الجوانب الأفقية للجسم تلغي بعضها البعض لأن الضغط على أي نقطة على جانب واحد يقابله ضغط مساوٍ له في المقدار ومعاكس في الاتجاه على الجانب المقابل عند نفس العمق.
4. محصلة القوى (قوة الطفو): قوة الطفو (Fb) هي القوة المحصلة الرأسية، أي الفرق بين القوة الصاعدة (F2) والقوة الهابطة (F1):
   Fb = F2 – F1
   Fb = [ρf * g * (d1 + h) * A] – [ρf * g * d1 * A]Fb = ρf * g * A * (d1 + h – d1)
   Fb = ρf * g * (A * h)

بما أن حجم متوازي المستطيلات (V) يساوي مساحة القاعدة (A) مضروبة في الارتفاع (h)، أي (V = A * h)، يمكننا التعويض في المعادلة:
Fb = ρf * g * V

وهذه المعادلة هي نفسها الصيغة الرياضية لمبدأ أرخميدس. لقد أثبتنا أن قوة الطفو تنشأ بشكل طبيعي من فرق الضغط بين أسفل الجسم وأعلاه. هذا الإثبات الرياضي يعزز فهمنا العميق للآلية الفيزيائية وراء مبدأ أرخميدس، ويؤكد أنه ليس مجرد ملاحظة تجريبية، بل نتيجة حتمية لقوانين الضغط في الموائع. إن هذا التحليل الدقيق هو ما يميز مبدأ أرخميدس كقانون فيزيائي متين.

العوامل الأساسية المؤثرة في مبدأ أرخميدس

وفقاً للصيغة الرياضية لمبدأ أرخميدس (Fb = ρf * V * g)، يمكننا تحديد عاملين رئيسيين يتحكمان في مقدار قوة الطفو التي يتعرض لها الجسم المغمور. إن فهم هذه العوامل ضروري لتطبيق مبدأ أرخميدس بشكل صحيح.

1. كثافة المائع (Density of the fluid – ρf):
   تلعب كثافة المائع دوراً محورياً في تحديد قوة الطفو. كلما زادت كثافة المائع، زادت قوة الطفو التي يؤثر بها على الجسم المغمور بنفس الحجم. هذا يفسر لماذا يطفو الشخص بسهولة أكبر في مياه البحر المالحة مقارنة بمياه البحيرة العذبة. مياه البحر أكثر كثافة بسبب الأملاح المذابة فيها، وبالتالي فإنها تولد قوة طفو أكبر لنفس حجم الجسم المغمور. وبالمثل، فإن الزئبق، وهو سائل فائق الكثافة، يمكنه أن يجعل الأجسام الفولاذية تطفو على سطحه. لذلك، فإن تطبيق مبدأ أرخميدس يتطلب معرفة دقيقة بكثافة المائع المعني.
2. حجم المائع المزاح (Volume of displaced fluid – V):
   هذا هو حجم الجزء المغمور من الجسم. من المهم التمييز بين حجم الجسم الكلي وحجم الجزء المغمور منه. فقوة الطفو لا تعتمد على وزن الجسم، أو شكله، أو المادة المصنوع منها، بل تعتمد بشكل مباشر وحصري على حجم الجزء المغمور في المائع. كلما زاد حجم الجزء المغمور من الجسم، زادت كمية المائع المزاح، وبالتالي زادت قوة الطفو المؤثرة عليه. هذا هو السبب في أن السفينة المصنوعة من الفولاذ (مادة عالية الكثافة) تطفو؛ فتصميمها المجوف يجعلها تزيح كمية هائلة من الماء، مما يولد قوة طفو كافية لمعادلة وزنها الضخم. إن هذا التفاعل بين الحجم والكثافة هو جوهر عمل مبدأ أرخميدس. إن تجاهل أي من هذين العاملين يؤدي إلى فهم منقوص لمبدأ أرخميدس.

حالات الطفو والغمر: تجليات مبدأ أرخميدس الثلاث

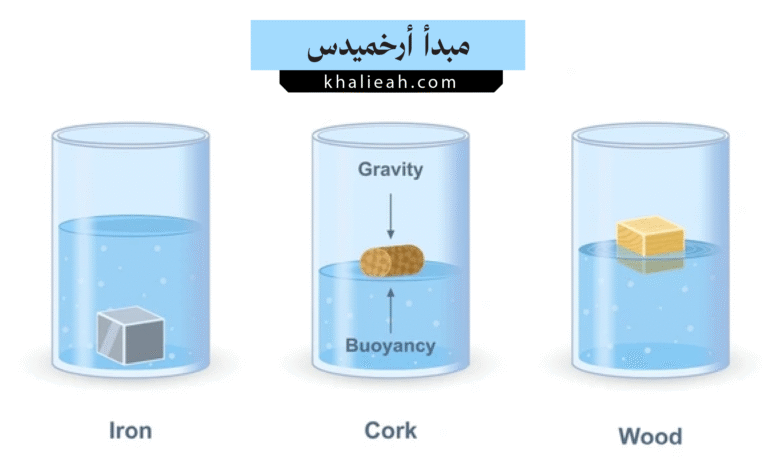
تحدد العلاقة بين قوة الطفو (Fb) المؤثرة على الجسم ووزن الجسم نفسه (Wg) ما إذا كان الجسم سيطفو، أو يغوص، أو يبقى معلقاً في المائع. يمكن تلخيص هذه الحالات الثلاث، التي تمثل تجليات مباشرة لمبدأ أرخميدس، على النحو التالي:

1. حالة الغوص (Sinking):
   يحدث الغوص عندما يكون وزن الجسم (Wg) أكبر من قوة الطفو (Fb). في هذه الحالة، تكون القوة المحصلة المؤثرة على الجسم متجهة إلى الأسفل، مما يؤدي إلى هبوطه نحو قاع المائع. رياضياً: Wg > Fb.
   يمكن التعبير عن هذا الشرط أيضاً باستخدام الكثافات. بما أن Wg = ρo * Vg * g (حيث ρo هي كثافة الجسم و Vg هو حجمه الكلي) و Fb = ρf * Vg * g (عندما يكون الجسم مغموراً بالكامل)، فإن شرط الغوص يصبح:
   ρo * Vg * g > ρf * Vg * g
   وبالتالي: ρo > ρf.
   أي أن الجسم يغوص إذا كانت كثافته أكبر من كثافة المائع. مثال على ذلك هو صخرة تُلقى في الماء. إن فهم هذه الحالة هو تطبيق مباشر لمبدأ أرخميدس.
2. حالة الطفو (Floating):
   يحدث الطفو عندما يكون وزن الجسم (Wg) مساوياً لقوة الطفو (Fb). في هذه الحالة، يكون الجسم مغموراً جزئياً فقط، ويستقر عند مستوى يكون فيه وزن المائع المزاح (الذي يحدده الجزء المغمور) مساوياً لوزن الجسم الكلي. رياضياً: Wg = Fb.
   في هذه الحالة، يكون حجم المائع المزاح (V) أقل من حجم الجسم الكلي (Vg). وهذا يعني أن كثافة الجسم الكلية (المتوسطة) يجب أن تكون أقل من كثافة المائع. ρo < ρf.
   مثال على ذلك قطعة من الخشب أو سفينة على سطح الماء. إن مبدأ أرخميدس يفسر بدقة كيف يمكن لأجسام هائلة أن تطفو طالما أن تصميمها يضمن إزاحة كمية كافية من الماء.
3. حالة الطفو المحايد (Neutral Buoyancy):
   تحدث هذه الحالة عندما يكون الجسم مغموراً بالكامل في المائع، ويكون وزنه مساوياً تماماً لقوة الطفو. رياضياً: Wg = Fb. في هذه الحالة، تكون القوة المحصلة على الجسم صفراً، وبالتالي يبقى الجسم معلقاً ومستقراً في أي عمق يوضع فيه داخل المائع، لا يرتفع ولا يهبط. يتحقق هذا الشرط عندما تكون كثافة الجسم مساوية تماماً لكثافة المائع: ρo = ρf.
   تعتبر هذه الحالة أساس عمل الغواصات، حيث تتحكم في طفوها عن طريق ضخ الماء إلى خزانات الصابورة (Ballast Tanks) أو تفريغها لضبط كثافتها المتوسطة لتتساوى مع كثافة الماء المحيط. هذا التحكم الدقيق هو تطبيق متقدم لمبدأ أرخميدس. إن هذه الحالات الثلاث توضح القدرة التنبؤية الهائلة التي يوفرها مبدأ أرخميدس.

تطبيقات عملية واسعة النطاق لمبدأ أرخميدس

يمتد تأثير مبدأ أرخميدس إلى ما هو أبعد من مجرد كونه قانوناً فيزيائياً نظرياً؛ فهو أساس لعدد لا يحصى من الاختراعات والتطبيقات الهندسية التي شكلت عالمنا الحديث.

• بناء السفن والقوارب: يعتبر تصميم السفن التطبيق الأكثر شهرة لمبدأ أرخميدس. على الرغم من أن السفن مصنوعة من الفولاذ، وهو أكثر كثافة من الماء بثماني مرات تقريباً، إلا أنها تطفو بسبب شكلها المجوف. هذا التجويف الكبير يجعل السفينة تزيح حجماً هائلاً من الماء. وفقاً لمبدأ أرخميدس، يولد هذا الماء المزاح قوة طفو عظيمة. يتم تصميم السفن بحيث تكون قوة الطفو هذه، عندما تكون السفينة محملة بالكامل، أكبر من أو تساوي وزن السفينة الكلي (الهيكل، المحركات، البضائع، إلخ). إن “خط التحميل” أو “خط بليمسول” (Plimsoll line) المرسوم على جانب السفينة هو مؤشر مرئي يضمن عدم تحميلها بشكل زائد، مما يحافظ على قوة طفو كافية لضمان سلامتها، وهو تطبيق مباشر لمعرفة مبدأ أرخميدس.
• الغواصات: تعتمد الغواصات في عملها على التحكم الدقيق في الطفو المحايد. يتم ذلك من خلال نظام معقد من خزانات الصابورة. لكي تغوص الغواصة، يتم ملء هذه الخزانات بمياه البحر، مما يزيد من وزنها الإجمالي وكثافتها المتوسطة حتى تصبح أكبر من قوة الطفو. ولكي ترتفع إلى السطح، يتم استخدام الهواء المضغوط لطرد المياه من الخزانات، مما يقلل من وزنها وتصبح قوة الطفو أكبر من الوزن. إن القدرة على التحكم الدقيق في العمق هي تجسيد للسيطرة الهندسية على مبدأ أرخميدس.
• المناطيد والبالونات الهوائية: يعمل مبدأ أرخميدس في الغازات بنفس الطريقة التي يعمل بها في السوائل، لأن الهواء يعتبر مائعاً. يرتفع المنطاد لأن الهواء الساخن أو الغاز الخفيف (مثل الهيليوم أو الهيدروجين) الذي يملأه يكون أقل كثافة من الهواء البارد المحيط به. يزيح المنطاد حجماً كبيراً من الهواء الخارجي الأكثر كثافة. ووفقاً لمبدأ أرخميدس، فإن وزن هذا الهواء المزاح (قوة الطفو) يكون أكبر من الوزن الكلي للمنطاد (بما في ذلك الغلاف والسلة والركاب)، مما يؤدي إلى ارتفاعه.
• الهيدروميتر (Hydrometer): هو أداة بسيطة تستخدم لقياس الكثافة النسبية (Specific Gravity) للسوائل، ويعتمد عمله كلياً على مبدأ أرخميدس. يتكون الهيدروميتر من أنبوب زجاجي مغلق، مثقل في الأسفل ليبقى عائماً بشكل رأسي. عندما يوضع في سائل، فإنه يغوص حتى يصبح وزن السائل الذي يزيحه مساوياً لوزنه الثابت. في السوائل عالية الكثافة، يزيح الهيدروميتر حجماً أقل من السائل ليطفو، وبالتالي يرتفع إلى مستوى أعلى. وفي السوائل منخفضة الكثافة، فإنه يغوص أعمق. التدريج الموجود على عنق الجهاز يسمح بقراءة الكثافة مباشرة، وهو تطبيق ذكي جداً لمبدأ أرخميدس.
• سترات النجاة: صُممت سترات النجاة لتكون ذات حجم كبير وكثافة منخفضة جداً (بسبب المواد المستخدمة مثل الرغوة أو الهواء المحبوس). عندما يرتديها شخص ما، فإنها تزيد من الحجم الإجمالي للجسم دون إضافة وزن كبير. هذا الحجم الإضافي يزيح كمية أكبر من الماء، مما يزيد بشكل كبير من قوة الطفو وفقاً لمبدأ أرخميدس، ويضمن بقاء رأس الشخص فوق سطح الماء حتى لو كان فاقداً للوعي. إن فهم مبدأ أرخميدس ينقذ الأرواح حرفياً في هذا السياق.

مبدأ أرخميدس في تخصصات علمية متقدمة

لا تقتصر أهمية مبدأ أرخميدس على التطبيقات الهندسية المباشرة، بل يمتد تأثيره ليشمل فهماً أعمق للظواهر في تخصصات علمية أخرى.

• الجيولوجيا وعلم توازن القشرة الأرضية (Isostasy): في الجيولوجيا، يُستخدم مفهوم مشابه لمبدأ أرخميدس لشرح توازن الكتل الصخرية الضخمة للقشرة الأرضية (Lithosphere) وهي “تطفو” على طبقة الوشاح (Asthenosphere) الأكثر كثافة وشبه السائلة. تماماً مثل جبل جليدي يطفو في الماء، فإن السلاسل الجبلية الشاهقة لها “جذور” عميقة تمتد داخل الوشاح لتحقيق التوازن. عندما تتآكل الجبال وتفقد كتلتها، فإنها ترتفع ببطء (Isostatic rebound) للحفاظ على هذا التوازن، وهو تطبيق على نطاق كوكبي لمبدأ أرخميدس.
• علم المواد: يُستخدم مبدأ أرخميدس بشكل روتيني في المختبرات لتحديد كثافة المواد الصلبة غير منتظمة الشكل بدقة. يتم ذلك عن طريق وزن المادة في الهواء أولاً، ثم وزنها وهي مغمورة بالكامل في سائل معروف الكثافة (مثل الماء). الفرق بين الوزنين (الوزن الظاهري) يساوي قوة الطفو، ومن خلال معرفة قوة الطفو، يمكن حساب حجم الجسم بدقة باستخدام مبدأ أرخميدس، ومن ثم حساب كثافته.
• علم المحيطات والأرصاد الجوية: يساعد مبدأ أرخميدس في فهم حركة الكتل المائية والهوائية. فالتيارات المائية الدافئة والأقل كثافة تميل إلى الارتفاع فوق المياه الباردة والأكثر كثافة. وبالمثل، في الغلاف الجوي، يرتفع الهواء الدافئ الأقل كثافة إلى الأعلى، مما يسبب تيارات الحمل الحراري التي تقود أنظمة الطقس العالمية. كل هذه الظواهر هي في جوهرها تجليات لمبدأ أرخميدس على نطاق واسع.

مفاهيم خاطئة شائعة حول مبدأ أرخميدس

على الرغم من بساطة مبدأ أرخميدس الظاهرية، إلا أن هناك بعض المفاهيم الخاطئة الشائعة التي يجب توضيحها:

1. الخطأ: الطفو يعتمد على وزن الجسم.
   الصواب: الطفو يعتمد على حجم المائع المزاح. جسمان لهما نفس الحجم ولكنهما يختلفان في الوزن (مثل كرة من الفولاذ وكرة من الألومنيوم بنفس الحجم) سيتعرضان لنفس قوة الطفو عند غمرهما بالكامل. ومع ذلك، فإن الكرة الفولاذية ستغوص لأن وزنها أكبر من قوة الطفو، بينما قد تطفو كرة الألومنيوم إذا كان وزنها أقل. إن مبدأ أرخميدس يربط الطفو بوزن المائع المزاح، وليس بوزن الجسم نفسه.
2. الخطأ: الأجسام الثقيلة تغوص والخفيفة تطفو.
   الصواب: العامل الحاسم هو الكثافة (الكتلة لكل وحدة حجم)، وليس الوزن. يمكن لسفينة تزن ملايين الأطنان أن تطفو، بينما تغوص عملة معدنية صغيرة تزن بضعة جرامات. السفينة تطفو لأن كثافتها المتوسطة (بما في ذلك التجويف الهوائي) أقل من كثافة الماء. العملة المعدنية تغوص لأن كثافتها أكبر بكثير من كثافة الماء. إن مبدأ أرخميدس يساعدنا على فهم أن العلاقة بين كثافة الجسم وكثافة المائع هي التي تحكم النتيجة.
3. الخطأ: شكل الجسم لا يؤثر على طفوه.
   الصواب: الشكل يؤثر بشكل حاسم على قدرة الجسم على إزاحة المائع. قطعة من الطين على شكل كرة ستغوص في الماء. ولكن إذا قمت بتشكيل نفس قطعة الطين على شكل وعاء مجوف، فإنها قد تطفو. لم يتغير وزن الطين أو كثافته، ولكن الشكل الجديد يسمح له بإزاحة حجم أكبر من الماء، مما يزيد من قوة الطفو وفقاً لمبدأ أرخميدس. هذا يوضح أن التلاعب بالشكل هو مفتاح تطبيقات مبدأ أرخميدس الهندسية.

الخاتمة: الإرث الخالد لمبدأ أرخميدس

في الختام، يظل مبدأ أرخميدس واحداً من أكثر المبادئ الفيزيائية أناقة وقوة وتأثيراً في تاريخ العلم. منذ اكتشافه في حوض استحمام في سيراقوسة القديمة، قدم هذا المبدأ تفسيراً أساسياً لظاهرة الطفو، وأصبح الأداة التي لا غنى عنها في تصميم السفن والغواصات والمناطيد، وفي فهم العمليات الجيولوجية والجوية المعقدة. إن بساطة نصه تخفي وراءها عمقاً فيزيائياً ورياضياً هائلاً، حيث يربط بين مفاهيم الحجم والكثافة والوزن والضغط في علاقة متناغمة. إن إرث مبدأ أرخميدس لا يكمن فقط في تطبيقاته العملية التي لا تعد ولا تحصى، بل أيضاً في كونه مثالاً ساطعاً على قوة الملاحظة العلمية والتفكير المنطقي في كشف أسرار الطبيعة. وبعد أكثر من ألفي عام، لا يزال مبدأ أرخميدس حجر زاوية يُدرّس في الفصول الدراسية ويُطبق في المختبرات والمصانع حول العالم، مما يؤكد على عبقرية الرجل الذي أهدى للعالم صرخة “يوريكا!” الخالدة. لا يمكن إنكار الأهمية القصوى لمبدأ أرخميدس في تشكيل فهمنا للعالم المادي. يثبت مبدأ أرخميدس أن القوانين الأساسية للطبيعة، بمجرد فهمها، يمكن تسخيرها لتحقيق إنجازات مذهلة. إن استمرار صلاحية مبدأ أرخميدس عبر العصور هو شهادة على طبيعة العلم التراكمية وعلى الإرث الدائم للعقول العظيمة.

الأسئلة الشائعة

1. ما هو النص العلمي الدقيق لمبدأ أرخميدس، وكيف تختلف قوة الطفو عن الوزن الظاهري؟

النص العلمي الدقيق لمبدأ أرخميدس ينص على أن “أي جسم مغمور كلياً أو جزئياً في مائع ساكن (سائل أو غاز) يتعرض لقوة دفع رأسية إلى الأعلى، تُعرف بقوة الطفو، مقدارها يساوي وزن المائع الذي يزيحه هذا الجسم”. رياضياً، تُعطى قوة الطفو (Fb) بالعلاقة: Fb = ρf * V * g، حيث ρf هي كثافة المائع، V هو حجم المائع المزاح، و g هو تسارع الجاذبية.

أما الفرق بين قوة الطفو والوزن الظاهري (Apparent Weight) فهو جوهري. قوة الطفو هي القوة الصاعدة التي يؤثر بها المائع على الجسم. في المقابل، الوزن الظاهري هو الوزن الذي يُظهره الميزان عند قياس وزن الجسم وهو مغمور في المائع. الوزن الظاهري هو نتيجة للفرق بين وزن الجسم الحقيقي (Wg) وقوة الطفو (Fb). يمكن التعبير عنه بالمعادلة: الوزن الظاهري = Wg – Fb. لذلك، فإن مبدأ أرخميدس يفسر لماذا تبدو الأجسام أخف وزناً عند غمرها في الماء؛ فالماء لا يقلل من وزن الجسم الفعلي (الذي يعتمد على كتلته والجاذبية)، بل يؤثر عليه بقوة طفو معاكسة للوزن، مما يقلل من القوة المحصلة النهائية التي نقيسها.

2. ما هو التفسير الفيزيائي لنشأة قوة الطفو التي يصفها مبدأ أرخميدس؟

تنشأ قوة الطفو التي يصفها مبدأ أرخميدس كنتيجة مباشرة لزيادة الضغط الهيدروستاتيكي (Hydrostatic Pressure) مع زيادة العمق في المائع. عندما يُغمر جسم في مائع، فإن المائع يؤثر بقوى ضغط على جميع أسطحه. وبما أن الضغط عند السطح السفلي للجسم (الأكثر عمقاً) يكون أعلى من الضغط عند سطحه العلوي (الأقل عمقاً)، فإن القوة التي يدفع بها المائع السطح السفلي إلى الأعلى تكون أكبر من القوة التي يضغط بها على السطح العلوي إلى الأسفل. محصلة هذا الفرق في القوى الرأسية هي قوة صافية متجهة إلى الأعلى، وهي ما نطلق عليه “قوة الطفو”. أما القوى الأفقية المؤثرة على جوانب الجسم، فإنها تلغي بعضها البعض. إذن، مبدأ أرخميدس ليس مجرد قانون تجريبي، بل هو نتيجة حتمية للطريقة التي يتوزع بها الضغط داخل المائع الساكن.

3. كيف يفسر مبدأ أرخميدس طفو سفينة فولاذية ضخمة، بينما تغوص قطعة صغيرة من الفولاذ؟

هذه المفارقة الظاهرية يتم تفسيرها بدقة من خلال مبدأ أرخميدس والتركيز على مفهومي الحجم المزاح والكثافة المتوسطة. قطعة الفولاذ الصغيرة مصمتة، وكثافتها (حوالي 7,850 كجم/م³) أكبر بكثير من كثافة الماء (حوالي 1,000 كجم/م³). عندما تغمر، فإن قوة الطفو المؤثرة عليها (وزن الماء المزاح الذي يساوي حجمها) تكون أقل بكثير من وزنها، فتغوص.

أما السفينة الفولاذية، فعلى الرغم من أنها مصنوعة من نفس المادة عالية الكثافة، إلا أن تصميمها مجوف ويحتوي على كمية هائلة من الهواء. هذا التصميم يجعل الكثافة المتوسطة للسفينة بأكملها (كتلة الفولاذ + الهواء مقسومة على الحجم الكلي للسفينة) أقل من كثافة الماء. الأهم من ذلك، أن هيكلها الضخم يزيح حجماً هائلاً من الماء. وفقاً لمبدأ أرخميدس، فإن قوة الطفو تساوي وزن هذه الكمية الهائلة من الماء المزاح. يتم تصميم السفينة بحيث تكون قوة الطفو هذه مساوية لوزن السفينة الكلي عندما تكون طافية، مما يحقق حالة التوازن. إذن، السر ليس في المادة، بل في الشكل الذي يسمح بإزاحة كمية كافية من المائع لتوليد قوة طفو تعادل الوزن.

4. ما هي العوامل المحددة التي تؤثر على مقدار قوة الطفو وفقاً لمبدأ أرخميدس؟ وهل لوزن الجسم أو شكله تأثير مباشر عليها؟

العوامل المحددة التي تؤثر مباشرة على مقدار قوة الطفو، كما تنص عليه معادلة مبدأ أرخميدس (Fb = ρf * V * g)، هي عاملان أساسيان:

1. كثافة المائع (ρf): كلما زادت كثافة المائع، زادت قوة الطفو لنفس الحجم المغمور.
2. حجم المائع المزاح (V): وهو حجم الجزء المغمور من الجسم. كلما غُمر جزء أكبر من الجسم، زادت قوة الطفو.

وزن الجسم وشكله ليس لهما تأثير مباشر على قوة الطفو. بمعنى أن جسمين مختلفين في الوزن والشكل ولكنهما يزيحان نفس حجم المائع سيتعرضان لنفس قوة الطفو تماماً. ومع ذلك، فإن للوزن والشكل تأثيراً غير مباشر وحاسماً في تحديد حالة الجسم النهائية (طفو أم غوص). فالوزن هو الذي تتم مقارنة قوة الطفو به (Wg مقابل Fb)، والشكل هو الذي يحدد مقدار الحجم الذي يمكن للجسم أن يزيحه بالنسبة لوزنه. لذا، لا يدخل وزن الجسم في حساب قوة الطفو نفسها، لكنه يحدد ناتج تفاعلها.

5. كيف يتم تطبيق مبدأ أرخميدس للتحكم في غوص وصعود الغواصات؟

تعتبر الغواصات مثالاً هندسياً متقدماً على التحكم الديناميكي في مبدأ أرخميدس. تعتمد الغواصة على نظام من الخزانات الكبيرة تسمى خزانات الصابورة (Ballast Tanks).

• للغوص: يتم فتح صمامات للسماح بدخول مياه البحر إلى هذه الخزانات. يؤدي هذا إلى زيادة الكتلة الكلية للغواصة (وبالتالي وزنها) دون تغيير حجمها الخارجي. عندما يصبح وزن الغواصة أكبر من قوة الطفو (التي تظل ثابتة طالما أن حجم الغواصة المغمورة ثابت)، تبدأ الغواصة بالغوص.
• للصعود: يتم استخدام هواء مضغوط مخزن في أسطوانات عالية الضغط لطرد المياه من خزانات الصابورة. هذا يقلل من الكتلة والوزن الكلي للغواصة. عندما يصبح وزنها أقل من قوة الطفو، تبدأ بالارتفاع نحو السطح.
• للحفاظ على عمق ثابت (الطفو المحايد): تضبط الغواصة كمية الماء في الخزانات بدقة شديدة حتى يتساوى وزنها الكلي تماماً مع قوة الطفو. في هذه الحالة، يمكنها البقاء معلقة في الماء دون أن تصعد أو تهبط، وهذا هو التطبيق الأمثل لمبدأ أرخميدس.

6. هل ينطبق مبدأ أرخميدس على الغازات مثل الهواء بنفس الطريقة التي ينطبق بها على السوائل؟

نعم، ينطبق مبدأ أرخميدس على الغازات بنفس الآلية الفيزيائية تماماً، لأن الغازات تُصنف ضمن الموائع (مواد قابلة للتدفق). أي جسم موجود في الهواء (أو أي غاز آخر) يتعرض لقوة طفو تساوي وزن الهواء الذي يزيحه. ومع ذلك، نظراً لأن كثافة الهواء منخفضة جداً (حوالي 1.225 كجم/م³ عند مستوى سطح البحر)، فإن قوة الطفو التي يولدها تكون صغيرة جداً وغير ملحوظة في العادة بالنسبة للأجسام الكثيفة. لكن هذه القوة تصبح حاسمة بالنسبة للأجسام ذات الكثافة المتوسطة المنخفضة جداً، مثل المناطيد والبالونات الهوائية. يرتفع المنطاد لأن الغاز بداخله (الهواء الساخن أو الهيليوم) أقل كثافة من الهواء المحيط، مما يجعل الكثافة المتوسطة للمنطاد بأكمله أقل من كثافة الهواء. هذا يؤدي إلى أن قوة الطفو (وزن الهواء الخارجي المزاح) تكون أكبر من الوزن الكلي للمنطاد، فيرتفع للأعلى تطبيقاً مباشراً لمبدأ أرخميدس.

7. ما هي العلاقة بين كثافة الجسم وكثافة المائع في تحديد ما إذا كان الجسم سيطفو أم يغوص أم يبقى معلقاً، استناداً إلى مبدأ أرخميدس؟

العلاقة بين كثافة الجسم (ρo) وكثافة المائع (ρf) هي المؤشر المباشر لتحديد حالة الجسم، وهي تلخيص عملي لمبدأ أرخميدس:

1. إذا كانت كثافة الجسم أكبر من كثافة المائع (ρo > ρf): سيغوص الجسم. في هذه الحالة، يكون وزن الجسم أكبر من وزن حجم مساوٍ له من المائع، مما يعني أن وزنه أكبر من أقصى قوة طفو يمكن أن يولدها المائع (عندما يكون الجسم مغموراً بالكامل).
2. إذا كانت كثافة الجسم أقل من كثافة المائع (ρo < ρf): سيطفو الجسم. سيغمر الجسم جزئياً فقط حتى يزيح كمية من المائع وزنها يساوي وزن الجسم الكلي، وعند هذه النقطة تتساوى قوة الطفو مع الوزن ويتحقق التوازن.
3. إذا كانت كثافة الجسم تساوي كثافة المائع (ρo = ρf): سيبقى الجسم معلقاً (طفو محايد). عندما يكون الجسم مغموراً بالكامل، فإن قوة الطفو المؤثرة عليه ستكون مساوية تماماً لوزنه. لذا، يمكنه البقاء مستقراً في أي عمق داخل المائع.

8. بعيداً عن قصة “يوريكا!” الشهيرة، كيف طبق أرخميدس اكتشافه عملياً للتحقق من ذهب التاج دون إتلافه؟

استخدم أرخميدس تطبيقاً عملياً وذكياً لمبدأه. كانت الطريقة الأكثر ترجيحاً هي استخدام ميزان حساس. أولاً، وضع التاج في إحدى كفتي الميزان ووضع كتلة من الذهب الخالص تساويه في الوزن تماماً في الكفة الأخرى، ليحقق التوازن في الهواء. بعد ذلك، قام بغمر كفتي الميزان معاً في حوض من الماء. لو كان التاج مصنوعاً من الذهب الخالص، لكان له نفس حجم كتلة الذهب، وبالتالي سيتعرض كلاهما لنفس قوة الطفو وفقاً لمبدأ أرخميدس، وكان الميزان سيبقى متوازناً. ولكن، بما أن التاج كان مخلوطاً بالفضة (الأقل كثافة)، كان حجمه أكبر من حجم كتلة الذهب المساوية له في الوزن. وبالتالي، أزاح التاج كمية أكبر من الماء وتعرض لقوة طفو أكبر. هذا جعل كفة التاج ترتفع إلى الأعلى، مما كسر التوازن وأثبت الغش. هذه الطريقة الدقيقة هي تجسيد لعبقرية تطبيق مبدأ أرخميدس.

9. ما هو مفهوم “الوزن الظاهري” (Apparent Weight) وكيف يرتبط مباشرةً بقوة الطفو الناتجة عن مبدأ أرخميدس؟

الوزن الظاهري هو القوة التي يسجلها جهاز قياس (مثل ميزان زنبركي) عند وزن جسم مغمور في مائع. هذا الوزن أقل من الوزن الحقيقي للجسم في الهواء. الارتباط المباشر يكمن في أن مقدار النقص في الوزن يساوي تماماً قوة الطفو التي يؤثر بها المائع على الجسم. يمكن صياغة ذلك كالتالي:

الوزن الظاهري = الوزن الحقيقي – قوة الطفو

هذه العلاقة هي في الواقع إعادة صياغة لمبدأ أرخميدس وتوفر طريقة عملية لقياس قوة الطفو. إذا قمت بوزن جسم في الهواء ثم وزنته في الماء، فإن الفرق بين القراءتين هو قوة الطفو. ومن خلال معرفة قوة الطفو، يمكن استخدام مبدأ أرخميدس لحساب حجم الجسم (V = Fb / (ρf * g))، وبالتالي تحديد كثافته بدقة، وهي تقنية أساسية في علم المواد.

10. هل يعمل مبدأ أرخميدس في بيئة منعدمة الجاذبية، مثل محطة الفضاء الدولية؟ ولماذا؟

لا، مبدأ أرخميدس لا يعمل في بيئة منعدمة الجاذبية (Zero-g). والسبب يكمن في أصل قوة الطفو نفسها. كما ذكرنا، تنشأ قوة الطفو بسبب فرق الضغط الناتج عن تأثير الجاذبية على المائع (الضغط يزداد مع العمق). في حالة انعدام الجاذبية، لا يوجد “أعلى” أو “أسفل”، والضغط داخل المائع يصبح متساوياً في جميع النقاط. وبالتالي، لا يوجد فرق في الضغط بين السطح العلوي والسفلي لجسم مغمور، مما يعني أن قوة الطفو تساوي صفراً. رياضياً، في معادلة مبدأ أرخميدس (Fb = ρf * V * g)، عندما يكون تسارع الجاذبية (g) صفراً، فإن قوة الطفو (Fb) تصبح صفراً أيضاً. لهذا السبب، في الفضاء، لا تطفو فقاعات الهواء في الماء إلى “الأعلى”، بل تبقى منتشرة في مكانها، ولا تطفو الأجسام الأقل كثافة.