الجذر التكعيبي: من الخصائص الجبرية الأساسية إلى التطبيقات الهندسية المتقدمة

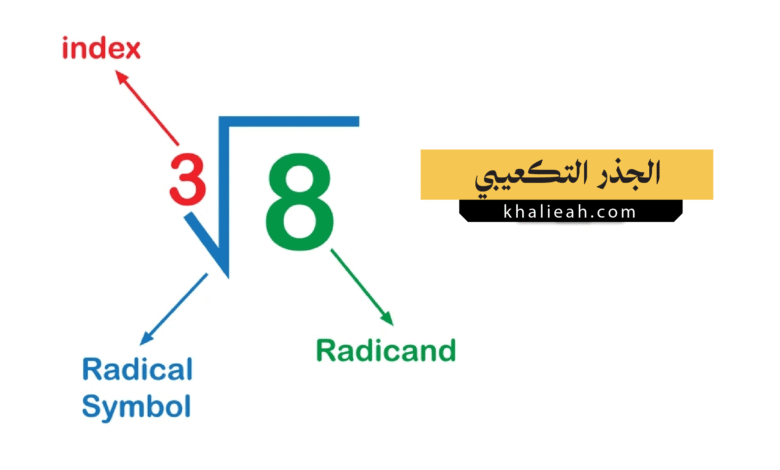
يمثل الجذر التكعيبي أحد المفاهيم الأساسية في علم الجبر والهندسة، حيث يشكل حجر زاوية في فهم العلاقات بين الأبعاد والأحجام. إن قدرته على عكس عملية الرفع إلى القوة الثالثة تمنحه دوراً فريداً في حل المعادلات وحساب المقادير الفيزيائية.

مقدمة

يُعرَّف الجذر التكعيبي (Cubic Root) لعدد ما بأنه القيمة التي إذا ضُربت في نفسها ثلاث مرات (أي تم تكعيبها)، فإنها تنتج العدد الأصلي. فإذا كان لدينا العدد a، فإن الجذر التكعيبي له، والذي يُرمز له بالرمز ³√a أو a^(1/3)، هو العدد b الذي يحقق المعادلة b³ = a. على سبيل المثال، الجذر التكعيبي للعدد 27 هو 3، لأن 3 × 3 × 3 = 27. وبالمثل، فإن الجذر التكعيبي للعدد -64 هو -4، لأن (-4) × (-4) × (-4) = -64. يختلف هذا المفهوم اختلافاً جوهرياً عن الجذر التربيعي، الذي يتعامل مع الأعداد المربعة، حيث إن مجال تعريف الجذر التكعيبي في مجموعة الأعداد الحقيقية يمتد ليشمل جميع الأعداد، سواء كانت موجبة أم سالبة أم صفراً، مما يمنحه مرونة رياضية وتطبيقية واسعة.

تتناول هذه المقالة مفهوم الجذر التكعيبي من منظور أكاديمي شامل، مستعرضةً أسسه التاريخية، وخصائصه الجبرية الدقيقة، وطرق حسابه المختلفة، وتطبيقاته العملية الواسعة في مجالات العلوم والهندسة، مع تسليط الضوء على دوره المحوري في النظم العددية المختلفة، بما في ذلك الأعداد المركبة. إن فهم عملية استخراج الجذر التكعيبي لا يقتصر على كونه مهارة حسابية، بل هو مدخل لفهم أعمق للبنى الرياضية التي تحكم العالم من حولنا.

الأسس التاريخية والمفاهيمية للجذر التكعيبي

لم يظهر مفهوم الجذر التكعيبي كمصطلح رياضي مجرد دفعة واحدة، بل تطور عبر قرون من الزمن نتيجة للحاجة العملية والفكرية لحل مسائل هندسية وجبرية معقدة. يمكن تتبع البدايات الأولى غير المباشرة لهذا المفهوم إلى الحضارات القديمة مثل البابليين والمصريين، الذين تعاملوا مع مسائل تتطلب حساب حجوم الأشكال ثلاثية الأبعاد كالمكعبات. على الرغم من أنهم لم يصيغوا نظرية رسمية حول الجذر التكعيبي، إلا أن جداولهم الرياضية كانت تحتوي على قيم لمكعبات الأعداد، والتي يمكن استخدامها بشكل عكسي لإيجاد القيمة التي تم تكعيبها. كانت هذه المحاولات بمثابة البذور الأولى التي نبت منها لاحقاً فهم أعمق لعملية إيجاد الجذر التكعيبي.

يُعد الإغريق القدماء من أبرز الحضارات التي واجهت تحديات رياضية عميقة مرتبطة بشكل مباشر بمفهوم الجذر التكعيبي. ولعل “مسألة ديلوس” (Delian Problem) أو “مضاعفة المكعب” هي المثال الأكثر شهرة. تقول الأسطورة إن وباءً ضرب أثينا، وأشار وحي دلفي إلى أن الوباء سينتهي إذا قام الأثينيون بمضاعفة حجم مذبح أبولو، الذي كان على شكل مكعب. أدرك علماء الرياضيات الإغريق بسرعة أن مضاعفة أضلاع المكعب ستؤدي إلى زيادة حجمه ثمانية أضعاف، وليس الضعف. لحل المسألة، كان عليهم إيجاد طول ضلع مكعب جديد حجمه ضعف حجم المكعب الأصلي. إذا كان طول ضلع المكعب الأصلي هو L وحجمه V = L³، فإن المكعب الجديد يجب أن يكون حجمه 2V. وبالتالي، فإن طول ضلعه الجديد L' يجب أن يحقق المعادلة (L')³ = 2L³، مما يعني أن L' = ³√2 * L. لقد كانت هذه المسألة بمثابة تحدٍ فكري هائل، حيث كان المطلوب هو إنشاء طول ³√2 باستخدام المسطرة والفرجار فقط، وهو ما أُثبت لاحقاً أنه مستحيل. ومع ذلك، فإن هذه المسألة حفزت تطوراً كبيراً في الهندسة وأدت إلى اكتشاف منحنيات جديدة وطرق مبتكرة للتعامل مع الكميات التي تتطلب استخلاص الجذر التكعيبي.

خلال العصر الذهبي للحضارة الإسلامية، قام علماء رياضيات بارزون مثل الخوارزمي وعمر الخيام بتقديم إسهامات جليلة في مجال الجبر وحل المعادلات. ركز الخيام بشكل خاص على حل المعادلات التكعيبية من الدرجة الثالثة (cubic equations) هندسياً عن طريق تقاطع القطوع المخروطية. إن حل هذه المعادلات يرتبط ارتباطاً وثيقاً بإيجاد الجذر التكعيبي، حيث إن أبسط صورة للمعادلة التكعيبية x³ - a = 0 حلها المباشر هو x = ³√a. لقد مهدت أعمالهم الطريق لعلماء الرياضيات في عصر النهضة الأوروبي مثل جيرولامو كاردانو ونيكولو فونتانا تارتاغليا، الذين طوروا صيغاً جبرية عامة لحل المعادلات التكعيبية في القرن السادس عشر. كانت هذه الصيغ، على الرغم من تعقيدها، تمثل إنجازاً رياضياً هائلاً، وكان الجذر التكعيبي عنصراً أساسياً لا غنى عنه في تركيبها. ومع تطور مفهوم الأعداد المركبة، أصبح من الممكن فهم الطبيعة الكاملة للمعادلات التكعيبية، حيث إن لكل عدد (باستثناء الصفر) ثلاثة جذور تكعيبية في مجموعة الأعداد المركبة، وهو ما أضاف بعداً جديداً وعمقاً لفهم عملية حساب الجذر التكعيبي.

الخصائص الجبرية والرياضية للجذر التكعيبي

يتمتع الجذر التكعيبي بمجموعة من الخصائص الجبرية التي تحكم سلوكه وتسهل التعامل معه في المعادلات والتعبيرات الرياضية. هذه الخصائص تنبع مباشرة من تعريفه كعملية عكسية للتكعيب، وهي متسقة عبر مختلف فروع الرياضيات. إن فهم هذه القواعد يمثل خطوة أساسية لإتقان استخدام الجذر التكعيبي في حل المسائل النظرية والتطبيقية.

تُعد هذه الخصائص أدوات قوية لتبسيط التعبيرات الرياضية المعقدة التي تتضمن الجذر التكعيبي، وتسمح بإجراء العمليات الحسابية بكفاءة ودقة. وفيما يلي استعراض لأهم هذه الخصائص مع أمثلة توضيحية:

• خاصية توزيع الجذر التكعيبي على الضرب:
  إن الجذر التكعيبي لحاصل ضرب عددين يساوي حاصل ضرب الجذر التكعيبي لكل منهما على حدة.
  الصيغة الرياضية: ³√(a * b) = ³√a * ³√b
  مثال: ³√(8 * 27) = ³√216 = 6. وباستخدام الخاصية: ³√8 * ³√27 = 2 * 3 = 6. هذه الخاصية مفيدة جداً في تبسيط الجذور للأعداد الكبيرة عن طريق تحليلها إلى عواملها الأولية.
• خاصية توزيع الجذر التكعيبي على القسمة:
  بشكل مشابه لخاصية الضرب، فإن الجذر التكعيبي لخارج قسمة عددين يساوي خارج قسمة الجذر التكعيبي لكل منهما.
  الصيغة الرياضية: ³√(a / b) = ³√a / ³√b (حيث b ≠ 0)
  مثال: ³√(125 / 8) = ³√15.625 = 2.5. وباستخدام الخاصية: ³√125 / ³√8 = 5 / 2 = 2.5. تسمح هذه الخاصية بمعالجة الكسور تحت الجذر بسهولة.
• العلاقة مع الأعداد السالبة:
  على عكس الجذر التربيعي، فإن الجذر التكعيبي لعدد حقيقي سالب هو عدد حقيقي سالب. يمكن إخراج الإشارة السالبة من تحت الجذر.
  الصيغة الرياضية: ³√(-a) = -³√a
  مثال: ³√(-64) = -4. ويمكن التحقق من ذلك أيضاً كالتالي: -³√64 = -4. هذه الميزة الفريدة تجعل الجذر التكعيبي قابلاً للتطبيق على جميع الأعداد الحقيقية دون قيود.
• العلاقة بالأسس الكسرية:
  يمكن التعبير عن عملية إيجاد الجذر التكعيبي باستخدام الأسس الكسرية، حيث إن أخذ الجذر التكعيبي لعدد ما يكافئ رفعه إلى القوة (1/3).
  الصيغة الرياضية: ³√a = a^(1/3)
  مثال: ³√27 = 27^(1/3) = 3. هذا التحويل مفيد للغاية عند التعامل مع قواعد الأسس المعقدة، حيث يمكنه تبسيط العمليات مثل (a^m)^(1/3) = a^(m/3).
• الجذر التكعيبي للصفر والواحد:
  إن الجذر التكعيبي للعدد صفر هو صفر (³√0 = 0)، والجذر التكعيبي للعدد واحد هو واحد (³√1 = 1). هذه هي الحالات الأساسية التي تنبني عليها العديد من البراهين الرياضية.

إن الإلمام بهذه الخصائص لا يسهل فقط الحسابات اليدوية، بل يوفر أيضاً فهماً أعمق لكيفية تفاعل الجذر التكعيبي مع العمليات الجبرية الأخرى، مما يجعله أداة رياضية مرنة وقوية.

الجذر التكعيبي في مجموعة الأعداد المركبة

عندما ننتقل من مجموعة الأعداد الحقيقية (Real Numbers) إلى مجموعة الأعداد المركبة (Complex Numbers)، يكتسب مفهوم الجذر التكعيبي أبعاداً جديدة وأكثر ثراءً. في حين أن أي عدد حقيقي له جذر تكعيبي حقيقي واحد فقط، فإن نظرية الجبر الأساسية (Fundamental Theorem of Algebra) تخبرنا أن أي عدد مركب غير صفري له بالضبط ثلاثة جذور تكعيبية في مجموعة الأعداد المركبة. هذا التوسع في المفهوم يحل العديد من المشكلات التي لا يمكن حلها ضمن نطاق الأعداد الحقيقية وحدها ويفتح الباب أمام فهم أعمق للدوال متعددة القيم.

لإيجاد الجذور التكعيبية الثلاثة لعدد مركب z، غالباً ما يتم التعبير عن هذا العدد بصيغته القطبية (Polar Form): z = r(cos(θ) + i sin(θ))، حيث r هي القيمة المطلقة (أو المقياس) للعدد z، و θ هي سعته (أو زاويته). باستخدام صيغة دي موافر (De Moivre’s Formula)، يمكننا اشتقاق صيغة عامة لإيجاد الجذور النونية لعدد مركب. بالنسبة للجذر التكعيبي (n=3)، تكون الجذور الثلاثة w_k على النحو التالي:
w_k = ³√r [cos((θ + 2πk) / 3) + i sin((θ + 2πk) / 3)]
حيث k تأخذ القيم 0، 1، 2.

عندما نطبق هذه الصيغة، نحصل على ثلاثة جذور مميزة. الجذر الأول (عند k=0) يُعرف غالباً بالجذر التكعيبي الرئيسي (Principal Cubic Root). أما الجذران الآخران (عند k=1 و k=2) فيكونان مركبين ومترافقين (complex conjugates) إذا كان العدد الأصلي حقيقياً. هذه الجذور الثلاثة، عند تمثيلها على المستوى المركب، تشكل رؤوس مثلث متساوي الأضلاع مركزه نقطة الأصل. على سبيل المثال، لنبحث عن الجذور التكعيبية للعدد 8. في مجموعة الأعداد الحقيقية، الجواب ببساطة هو 2. أما في مجموعة الأعداد المركبة، فالعدد 8 يمكن كتابته بالشكل القطبي 8(cos(0) + i sin(0)). بتطبيق الصيغة، نحصل على:

• عند k=0: ³√8 [cos(0/3) + i sin(0/3)] = 2(1 + 0i) = 2. هذا هو الجذر الحقيقي المألوف.
• عند k=1: ³√8 [cos(2π/3) + i sin(2π/3)] = 2(-1/2 + i√3/2) = -1 + i√3.
• عند k=2: ³√8 [cos(4π/3) + i sin(4π/3)] = 2(-1/2 - i√3/2) = -1 - i√3.
  إذن، الجذور التكعيبية الثلاثة للعدد 8 هي: 2، -1 + i√3، و -1 - i√3. إن اكتشاف هذه الجذور المركبة كان له تأثير عميق على تطور الرياضيات، خاصة في حل المعادلات التكعيبية التي قد تكون لها حلول حقيقية ولكن تتطلب خطوات وسطية تتضمن أعداداً مركبة (casus irreducibilis). إن فهم كيفية حساب الجذر التكعيبي في هذا السياق الأوسع ضروري في مجالات متقدمة مثل الهندسة الكهربائية، ومعالجة الإشارات، وفيزياء الكم، حيث تلعب الأعداد المركبة دوراً أساسياً.

طرق حساب الجذر التكعيبي

على الرغم من أن الآلات الحاسبة الحديثة والبرمجيات الحاسوبية توفر طريقة فورية لحساب الجذر التكعيبي لأي عدد، فإن فهم الطرق الحسابية والتقديرية التي تكمن وراء هذه العملية يظل ذا قيمة أكاديمية وعملية كبيرة. تاريخياً، تم تطوير العديد من الخوارزميات والتقنيات لإيجاد قيمة الجذر التكعيبي بدقة متفاوتة، بدءاً من الطرق اليدوية البسيطة وصولاً إلى الخوارزميات التكرارية المعقدة.

إن اختيار الطريقة المناسبة يعتمد على طبيعة العدد المطلوب حساب جذره (هل هو مكعب كامل أم لا؟) ومستوى الدقة المطلوب. فيما يلي بعض الطرق الرئيسية المستخدمة في حساب الجذر التكعيبي:

1. التحليل إلى العوامل الأولية (Prime Factorization):
   هذه الطريقة فعالة جداً للأعداد التي هي مكعبات كاملة. تتضمن العملية تحليل العدد إلى عوامله الأولية، ثم تجميع هذه العوامل في مجموعات من ثلاثة عوامل متماثلة.
   • الخطوة الأولى: قم بتحليل العدد إلى عوامله الأولية. على سبيل المثال، العدد 1728.
     1728 = 2 * 864 = 2 * 2 * 432 = ... = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3
   • الخطوة الثانية: أعد كتابة العوامل في صورة أسية: 1728 = 2^6 * 3^3.
   • الخطوة الثالثة: استخرج الجذر التكعيبي عن طريق قسمة كل أس على 3:
     ³√1728 = ³√(2^6 * 3^3) = 2^(6/3) * 3^(3/3) = 2^2 * 3^1 = 4 * 3 = 12.
     هذه الطريقة دقيقة وتوفر الإجابة الصحيحة للمكعبات الكاملة، ولكنها غير عملية للأعداد التي ليست مكعبات كاملة.
2. التقدير والتحسين (Estimation and Refinement):
   تعتمد هذه الطريقة على الحدس الرياضي والتقريب التدريجي. يمكن استخدامها لتقدير الجذر التكعيبي لأي عدد.
   • الخطوة الأولى: ابحث عن أقرب مكعبين كاملين يقع العدد بينهما. لحساب ³√100، نعلم أن 4³ = 64 و 5³ = 125. إذن، قيمة الجذر التكعيبي للعدد 100 تقع بين 4 و 5.
   • الخطوة الثانية: قم بتخمين أولي. بما أن 100 أقرب إلى 125 منها إلى 64، يمكننا تخمين قيمة مثل 4.6.
   • الخطوة الثالثة: اختبر التخمين بتكعيبه: 4.6³ = 97.336. هذه القيمة قريبة جداً من 100 ولكنها أقل.
   • الخطوة الرابعة: قم بتحسين التخمين. لنجرب قيمة أعلى قليلاً، مثل 4.64. 4.64³ ≈ 99.88. هذا تقدير أفضل بكثير. يمكن تكرار هذه العملية للوصول إلى الدقة المطلوبة.
3. الخوارزميات العددية (Numerical Algorithms):
   للحصول على دقة عالية، تُستخدم خوارزميات تكرارية قوية. أشهرها هي طريقة نيوتن-رافسون (Newton-Raphson method) لإيجاد جذور دالة. لإيجاد الجذر التكعيبي للعدد a، نبحث عن جذر الدالة f(x) = x³ - a.
   • الصيغة التكرارية: x_(n+1) = x_n - f(x_n) / f'(x_n)
   • بما أن f'(x) = 3x²، تصبح الصيغة الخاصة بإيجاد الجذر التكعيبي:
     x_(n+1) = x_n - (x_n³ - a) / (3x_n²) = (2x_n + a / x_n² ) / 3
   • التطبيق: لإيجاد ³√100، لنبدأ بتخمين أولي x_0 = 4.6.
     التكرار الأول: x_1 = (2*4.6 + 100 / 4.6²) / 3 ≈ (9.2 + 4.726) / 3 ≈ 4.642
     التكرار الثاني: x_2 = (2*4.642 + 100 / 4.642²) / 3 ≈ 4.64158
     تتميز هذه الطريقة بتقاربها السريع جداً نحو الحل الصحيح، وهي الأساس الذي تعمل به معظم الآلات الحاسبة الرقمية عند حساب الجذر التكعيبي.

تطبيقات الجذر التكعيبي في العلوم والهندسة

لا يقتصر وجود الجذر التكعيبي على الكتب والنظريات الرياضية، بل يمتد تأثيره إلى مجموعة واسعة من التطبيقات العملية في مجالات العلوم الطبيعية والهندسة. إن قدرته على ربط الكميات أحادية البعد (مثل الطول) بالكميات ثلاثية الأبعاد (مثل الحجم) تجعله أداة لا غنى عنها في النمذجة والتحليل. ففي كل مرة نحتاج فيها إلى استنتاج بُعد خطي من قياس حجمي، يظهر الجذر التكعيبي كحل رياضي ضروري.

في مجال الهندسة المعمارية والمدنية، يعتبر حساب الجذر التكعيبي عملية أساسية. عند تصميم المباني والخزانات والهياكل، يكون الحجم غالباً هو المتغير المحدد (على سبيل المثال، سعة خزان ماء أو حجم غرفة). لتحديد الأبعاد الخطية (الطول، العرض، الارتفاع) التي تحقق هذا الحجم، خاصة في الأشكال المنتظمة مثل المكعب، فإن حساب الجذر التكعيبي للحجم المستهدف يعطينا مباشرةً طول الضلع المطلوب. على سبيل المثال، لتصميم خزان مكعب الشكل يسع 27,000 لتر (أو 27 متراً مكعباً)، يجب أن يكون طول ضلعه هو الجذر التكعيبي للعدد 27، أي 3 أمتار. هذا المبدأ يمتد إلى تصميم الأجزاء الميكانيكية، حيث يرتبط حجم المادة بكتلتها وقوتها، ويتطلب تحديد أبعادها حسابات تتضمن الجذر التكعيبي.

في الفيزياء، وخصوصاً في علم الفلك والميكانيكا السماوية، يلعب الجذر التكعيبي دوراً محورياً. ينص قانون كبلر الثالث للمدارات الكوكبية على أن مربع الفترة المدارية لكوكب (T) يتناسب طردياً مع مكعب متوسط بعده عن الشمس (a)، أو T² ∝ a³. إذا أردنا حساب متوسط بعد كوكب عن الشمس بمعرفة فترته المدارية، فإننا نحتاج إلى إعادة ترتيب المعادلة لتصبح a ∝ ³√(T²). هذا يعني أن عملية إيجاد المسافة المدارية تعتمد بشكل مباشر على الجذر التكعيبي. وفي الديناميكا الحرارية، ترتبط بعض الخصائص، مثل نصف القطر الذري الفعال في نماذج الغازات، بحجم الجسيمات، مما يستدعي استخدام الجذر التكعيبي لربط هذه المقاييس.

في الكيمياء وعلوم المواد، يظهر الجذر التكعيبي عند دراسة الهياكل البلورية. تتจัด الذرات في العديد من المواد الصلبة في شبكات بلورية منتظمة، مثل المكعب متمركز الجسم (BCC) أو المكعب متمركز الوجه (FCC). حجم وحدة الخلية (unit cell) في هذه الهياكل هو حجم مكعب، ويرتبط مباشرة بالمسافة بين الذرات. لحساب ثابت الشبكة (lattice constant)، وهو طول ضلع وحدة الخلية، من الحجم الذي تشغله الذرات (والذي يمكن تقديره من كثافة المادة)، فإننا نلجأ إلى عملية حساب الجذر التكعيبي. هذا يسمح للعلماء بفهم الخصائص الفيزيائية للمواد، مثل الصلابة والمرونة، بناءً على ترتيبها الذري الدقيق. إن أهمية الجذر التكعيبي في هذه المجالات تبرز كونه جسراً رياضياً يربط بين العالم المجهري (الذري) والعالم العياني (خصائص المادة).

الفروقات الجوهرية بين الجذر التكعيبي والجذر التربيعي

على الرغم من أن الجذر التكعيبي والجذر التربيعي ينتميان إلى عائلة “الجذور” الرياضية، إلا أنهما يمتلكان خصائص رياضية وسلوكيات مختلفة بشكل كبير، مما يؤدي إلى تطبيقات واستخدامات متباينة. إن فهم هذه الفروقات أمر بالغ الأهمية لتجنب الأخطاء المفاهيمية وتطبيق المفهوم الصحيح في السياق المناسب. الاختلافات لا تقتصر على أن أحدهما يتعامل مع القوة الثانية والآخر مع القوة الثالثة، بل تمتد إلى مجال التعريف، وطبيعة النتائج، والتفسير الهندسي لكل منهما.

أحد أبرز الفروقات وأكثرها أهمية يكمن في مجال التعريف (Domain) في مجموعة الأعداد الحقيقية. الجذر التربيعي معرّف فقط للأعداد غير السالبة (الصفر والأعداد الموجبة). لا يمكن إيجاد جذر تربيعي حقيقي لعدد سالب، حيث إن تربيع أي عدد حقيقي (موجب أو سالب) ينتج عنه دائماً قيمة موجبة. على النقيض من ذلك، فإن الجذر التكعيبي معرّف لجميع الأعداد الحقيقية دون استثناء. يمكننا إيجاد الجذر التكعيبي لعدد موجب (النتيجة موجبة)، ولعدد سالب (النتيجة سالبة)، وللصفر (النتيجة صفر). هذه الخاصية تجعل دالة الجذر التكعيبي دالة مستمرة ومتصلة على خط الأعداد الحقيقية بأكمله، بينما دالة الجذر التربيعي تبدأ من الصفر وتمتد في الاتجاه الموجب فقط.

الفرق الجوهري الثاني يتعلق بعدد الحلول الحقيقية. لكل عدد حقيقي موجب، يوجد جذر تربيعي موجب واحد فقط (يُعرف بالجذر الرئيسي). أما بالنسبة للمعادلة x² = a (حيث a > 0)، فلها حلان حقيقيان: +√a و -√a. في المقابل، لكل عدد حقيقي (موجب أو سالب)، يوجد جذر تكعيبي حقيقي واحد فقط. المعادلة x³ = a لها حل حقيقي فريد دائماً. على سبيل المثال، x³ = 8 لها حل حقيقي واحد فقط وهو x=2. وكذلك x³ = -8 لها حل حقيقي واحد فقط وهو x=-2. هذا التباين في عدد الحلول الحقيقية يعكس اختلافاً عميقاً في بنية الدوال الأسية الزوجية والفردية، حيث إن الدالة f(x) = x³ هي دالة واحد لواحد (one-to-one)، بينما الدالة g(x) = x² ليست كذلك.

من الناحية الهندسية، يمثل كل جذر مفهوماً مختلفاً تماماً. يرتبط الجذر التربيعي بمساحة المربع؛ فالجذر التربيعي للمساحة A يعطي طول ضلع المربع L. إنه يربط بين كمية ثنائية الأبعاد (المساحة) وكمية أحادية البعد (الطول). أما الجذر التكعيبي، فيرتبط بحجم المكعب؛ فالجذر التكعيبي للحجم V يعطي طول ضلع المكعب L. إنه يربط بين كمية ثلاثية الأبعاد (الحجم) وكمية أحادية البعد (الطول). هذا التفسير الهندسي يوضح لماذا يظهر الجذر التكعيبي بشكل طبيعي في المسائل المتعلقة بالأحجام والأبعاد الفراغية، بينما يكثر استخدام الجذر التربيعي في المسائل المتعلقة بالمساحات والمسافات في المستوى (مثل نظرية فيثاغورس). إن التمييز بين هذين المفهومين أساسي للنمذجة الرياضية الدقيقة للظواهر الفيزيائية والهندسية.

خاتمة

في ختام هذا التحليل المفصل، يتضح أن الجذر التكعيبي ليس مجرد عملية حسابية بسيطة، بل هو مفهوم رياضي عميق الجذور وواسع التأثير. لقد تتبعنا رحلته من التحديات الهندسية القديمة، مثل مسألة مضاعفة المكعب، إلى دوره المركزي في الصيغ الجبرية المتقدمة لحل المعادلات التكعيبية. إن خصائصه الجبرية الفريدة، خاصة قدرته على التعامل مع الأعداد السالبة بسلاسة، تميزه عن نظيره الجذر التربيعي وتمنحه مجالاً تطبيقياً شاملاً في مجموعة الأعداد الحقيقية. كما أن استكشاف مفهوم الجذر التكعيبي في فضاء الأعداد المركبة كشف عن بنية أكثر تعقيداً وثراءً، حيث لكل عدد ثلاثة جذور تكعيبية تشكل رؤوس مثلث متساوي الأضلاع، مما يبرهن على تكامل وتناغم الفروع المختلفة للرياضيات.

إن الطرق المتعددة لحسابه، من التحليل البسيط إلى العوامل الأولية إلى الخوارزميات التكرارية القوية مثل طريقة نيوتن، تسلط الضوء على تطور الفكر الرياضي والحاسوبي عبر العصور. والأهم من ذلك، أن تطبيقاته العملية في الفيزياء، والهندسة، والكيمياء، والفلك تؤكد على أن الجذر التكعيبي ليس مفهوماً نظرياً منعزلاً، بل هو أداة تحليلية لا غنى عنها لفهم ووصف العالم المادي من حولنا، من حركة الكواكب في مداراتها إلى بنية الذرات في المواد الصلبة. في نهاية المطاف، يظل الجذر التكعيبي شاهداً على قدرة الرياضيات على توفير لغة دقيقة ونماذج قوية لحل المشكلات الأكثر تعقيداً في العلم والتكنولوجيا.

أسئلة شائعة وإجاباتها

1. ما هو التعريف الرياضي الدقيق لمفهوم الجذر التكعيبي؟
الجذر التكعيبي لعدد a هو العدد b الذي إذا تم رفعه للقوة الثالثة (أي b³) فإنه يساوي a. رياضياً، إذا كان b³ = a، فإن b = ³√a. وهو يمثل العملية العكسية لعملية التكعيب.

2. لماذا يمكن حساب الجذر التكعيبي للأعداد السالبة بينما لا يمكن ذلك للجذر التربيعي في مجموعة الأعداد الحقيقية؟
لأن تكعيب أي عدد حقيقي سالب ينتج عنه عدد سالب (مثلاً، (-2)³ = -8). لذلك، لكل عدد حقيقي سالب يوجد جذر تكعيبي حقيقي سالب مقابل له. في المقابل، تربيع أي عدد حقيقي (سواء كان موجباً أو سالباً) ينتج عنه دائماً عدد موجب، مما يجعل من المستحيل إيجاد جذر تربيعي حقيقي لعدد سالب.

3. كم عدد الجذور التكعيبية الموجودة لأي عدد؟
في مجموعة الأعداد الحقيقية، لكل عدد جذر تكعيبي حقيقي واحد فقط. أما في مجموعة الأعداد المركبة، فإن لكل عدد غير صفري ثلاثة جذور تكعيبية بالضبط: جذر حقيقي واحد وجذران مركبان مترافقان (إذا كان العدد الأصلي حقيقياً)، أو ثلاثة جذور مركبة.

4. ما هي العلاقة بين الجذر التكعيبي والأسس الكسرية؟
عملية إيجاد الجذر التكعيبي لعدد ما تكافئ تماماً عملية رفع هذا العدد إلى القوة (1/3). هذه العلاقة تُكتب رياضياً على الصورة ³√a = a^(1/3)، وهي خاصية مفيدة جداً في تبسيط التعبيرات الجبرية المعقدة التي تتضمن جذوراً وأسساً.

5. ما هو التفسير الهندسي لمفهوم الجذر التكعيبي؟
هندسياً، يمثل الجذر التكعيبي العلاقة بين حجم المكعب وطول ضلعه. إذا كان حجم المكعب هو V، فإن طول ضلعه L يساوي الجذر التكعيبي للحجم (L = ³√V). إنه يربط بين كمية ثلاثية الأبعاد (الحجم) وكمية أحادية البعد (الطول).

6. هل الجذر التكعيبي لعدد غير نسبي هو دائماً عدد غير نسبي؟
نعم، إذا كان العدد a عدداً غير نسبي، فإن الجذر التكعيبي له ³√a يكون أيضاً عدداً غير نسبي. وينطبق هذا أيضاً على المكعبات غير الكاملة للأعداد النسبية؛ على سبيل المثال، الجذر التكعيبي للعدد 2 هو عدد غير نسبي.

7. كيف يتم تقدير قيمة الجذر التكعيبي لعدد ليس مكعباً كاملاً؟
يمكن تقدير القيمة عن طريق تحديد أقرب مكعبين كاملين يقع العدد بينهما. على سبيل المثال، لتقدير ³√30، نعلم أن 3³ = 27 و 4³ = 64. بما أن 30 قريب جداً من 27، فإن قيمة الجذر التكعيبي ستكون أعلى بقليل من 3، ربما حوالي 3.1.

8. ما هي أشهر خوارزمية حاسوبية لحساب الجذر التكعيبي بدقة عالية؟
تُعد طريقة نيوتن-رافسون (Newton-Raphson method) من أشهر وأكفأ الخوارزميات العددية المستخدمة. وهي طريقة تكرارية تقترب من الحل الصحيح بسرعة فائقة، وتُستخدم في معظم الآلات الحاسبة والبرمجيات الرياضية لإيجاد قيمة الجذر التكعيبي بدقة.

9. ما هو الجذر التكعيبي الرئيسي (Principal Root)؟
عند التعامل مع الأعداد المركبة، يكون هناك ثلاثة جذور تكعيبية. يُطلق مصطلح “الجذر التكعيبي الرئيسي” على الجذر الذي له أصغر سعة (argument) غير سالبة عند تمثيله في المستوى القطبي. في حالة الأعداد الحقيقية، يكون الجذر الرئيسي هو الجذر الحقيقي الوحيد.

10. هل تتوزع عملية أخذ الجذر التكعيبي على الجمع والطرح؟
لا، عملية أخذ الجذر التكعيبي لا تتوزع على عمليتي الجمع أو الطرح. هذا يعني أن ³√(a + b) لا يساوي ³√a + ³√b. هذه إحدى المغالطات الجبرية الشائعة التي يجب تجنبها.

---

تمارين ومسائل محلولة

تمارين للمستوى العام

التمرين 1: أوجد قيمة ³√(-125).
الحل: نبحث عن العدد الذي إذا ضُرب في نفسه ثلاث مرات يساوي -125.
بما أن 5 × 5 × 5 = 125، فإن (-5) × (-5) × (-5) = -125.
إذن، ³√(-125) = -5.

التمرين 2: بسّط التعبير التالي: ³√(64 * 1000).
الحل: باستخدام خاصية توزيع الجذر على الضرب:
³√(64 * 1000) = ³√64 * ³√1000
³√64 = 4
³√1000 = 10
إذن، 4 * 10 = 40.

التمرين 3: حل المعادلة التالية لإيجاد قيمة x: x³ + 8 = 35.
الحل:

1. اطرح 8 من كلا الطرفين: x³ = 35 - 8
2. x³ = 27
3. خذ الجذر التكعيبي لكلا الطرفين: x = ³√27
4. x = 3.

التمرين 4: أوجد قيمة ³√(216 / 729).
الحل: باستخدام خاصية توزيع الجذر على القسمة:
³√(216 / 729) = ³√216 / ³√729
³√216 = 6
³√729 = 9
إذن، القيمة هي 6 / 9، والتي يمكن تبسيطها إلى 2 / 3.

التمرين 5: حجم صندوق مكعب الشكل هو 512 سم مكعب. ما هو طول ضلع الصندوق؟
الحل:
حجم المكعب V = L³، حيث L هو طول الضلع.
L = ³√V
L = ³√512
L = 8 سم.

تمارين للمستوى المتقدم

التمرين 6: بسّط التعبير الجبري التالي: ³√(54x⁷y¹⁰).
الحل:

1. حلل العدد والمتغيرات إلى عوامل تكعيبية وغير تكعيبية:
   54 = 27 * 2 = 3³ * 2
x⁷ = x⁶ * x = (x²)³ * x
y¹⁰ = y⁹ * y = (y³)³ * y
2. أعد كتابة التعبير: ³√( (3³ * (x²)³ * (y³)³) * (2 * x * y) )
3. استخرج العوامل التكعيبية من تحت الجذر: 3x²y³ * ³√(2xy).

التمرين 7: حل المعادلة التالية: ³√(4x + 3) - 5 = -2.
الحل:

1. أضف 5 إلى كلا الطرفين: ³√(4x + 3) = 3.
2. كعّب كلا الطرفين للتخلص من الجذر: (³√(4x + 3))³ = 3³.
3. 4x + 3 = 27.
4. اطرح 3 من كلا الطرفين: 4x = 24.
5. اقسم على 4: x = 6.

التمرين 8: أوجد قيمة (³√16) / (³√2).
الحل:
باستخدام خاصية دمج القسمة تحت جذر واحد:
(³√16) / (³√2) = ³√(16 / 2)
= ³√8
= 2.

التمرين 9: إذا كان a = ³√5، فأوجد قيمة a⁹ بدون استخدام آلة حاسبة.
الحل:

1. يمكن كتابة a⁹ على الصورة (a³)³.
2. نعلم أن a = ³√5.
3. إذن، a³ = (³√5)³ = 5.
4. بالتعويض في التعبير الأصلي: a⁹ = (a³)³ = 5³ = 125.

التمرين 10: أوجد جميع الجذور التكعيبية المركبة للعدد z = -27.
الحل:

1. اكتب العدد z = -27 بالصيغة القطبية: z = 27(cos(π) + i sin(π)).
2. باستخدام صيغة دي موافر للجذور w_k = ³√r [cos((θ + 2πk) / 3) + i sin((θ + 2πk) / 3)] حيث k = 0, 1, 2.
3. هنا r = 27 و θ = π. ³√r = 3.
4. لـ k = 0:
   w₀ = 3[cos(π/3) + i sin(π/3)] = 3(1/2 + i√3/2) = 3/2 + i(3√3/2).
5. لـ k = 1:
   w₁ = 3[cos((π + 2π)/3) + i sin((π + 2π)/3)] = 3[cos(π) + i sin(π)] = 3(-1 + 0i) = -3. (الجذر الحقيقي)
6. لـ k = 2:
   w₂ = 3[cos((π + 4π)/3) + i sin((π + 4π)/3)] = 3[cos(5π/3) + i sin(5π/3)] = 3(1/2 - i√3/2) = 3/2 - i(3√3/2).
   إذن، الجذور الثلاثة هي: -3، 3/2 + i(3√3/2)، و 3/2 - i(3√3/2).