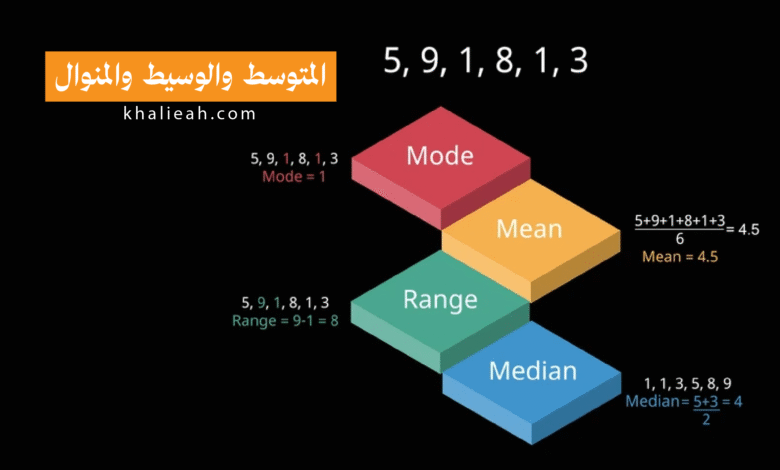
المتوسط، الوسيط، والمنوال: فهم المقاييس الأساسية لوصف بياناتك

في عالم اليوم الذي تغمره البيانات، أصبحت القدرة على فهم وتفسير المعلومات الرقمية مهارة لا غنى عنها في مختلف التخصصات، من العلوم الطبيعية والهندسية إلى الاقتصاد والعلوم الاجتماعية والطب. قبل أن نتمكن من بناء نماذج تنبؤية معقدة أو إجراء اختبارات فرضيات متقدمة، يجب علينا أولاً أن نبدأ من الأساس: وصف البيانات التي بين أيدينا. وهنا يأتي دور الإحصاء الوصفي (Descriptive Statistics)، وهو الفرع من علم الإحصاء الذي يهتم بتلخيص وتنظيم ووصف الخصائص الرئيسية لمجموعة من البيانات. وفي قلب الإحصاء الوصفي تكمن “مقاييس النزعة المركزية” (Measures of Central Tendency)، وهي قيم إحصائية تحاول تحديد القيمة “النموذجية” أو “المركزية” ضمن مجموعة البيانات.

إن الهدف من مقاييس النزعة المركزية هو توفير قيمة واحدة تمثل أفضل تلخيص ممكن لمجموعة كاملة من المشاهدات. تخيل أنك مدير مدرسة وتريد معرفة الأداء العام للطلاب في اختبار الرياضيات؛ بدلاً من النظر في درجات مئات الطلاب بشكل فردي، يمكنك استخدام قيمة واحدة مثل “متوسط الدرجات” لتعطيك فكرة سريعة عن أداء الفصل. هذه المقاييس هي أدواتنا الأولى لاستكشاف البيانات، وتساعدنا على تكوين فهم أولي لطبيعتها وتوزيعها.

الأبطال الثلاثة الرئيسيون في هذا المجال هم: المتوسط الحسابي (The Mean)، والوسيط (The Median)، والمنوال (The Mode). على الرغم من أن هذه المصطلحات قد تبدو بسيطة، إلا أن كلاً منها يقدم منظوراً فريداً للبيانات، ولكل منها نقاط قوته وضعفه، وحالات استخدام مثالية. إن الفهم العميق لهذه المقاييس الثلاثة، ومتى وكيف نستخدم كلاً منها، هو حجر الزاوية لأي تحليل بيانات سليم. هذه المقالة الأكاديمية ستغوص بعمق في كل من هذه المقاييس، مستعرضة تعريفاتها، طرق حسابها، خصائصها الرياضية، نقاط قوتها وضعفها، وتأثير شكل توزيع البيانات عليها، مع تقديم أمثلة عملية توضح أهميتها في العالم الحقيقي.

H2: المتوسط الحسابي (The Mean): مركز ثقل البيانات

المتوسط الحسابي، والذي يُشار إليه غالباً بكلمة “المعدل” (Average) في الحياة اليومية، هو أشهر مقاييس النزعة المركزية وأكثرها استخداماً على الإطلاق. رياضياً، يُعرّف المتوسط الحسابي بأنه مجموع كل القيم في مجموعة البيانات مقسوماً على عدد هذه القيم. إنه يمثل “نقطة التوازن” أو “مركز الثقل” للبيانات؛ فلو تخيلنا أن كل قيمة في البيانات هي وزن موضوع على مسطرة، فإن المتوسط الحسابي هو النقطة التي ستتوازن عندها المسطرة تماماً.

الصيغة الرياضية وطريقة الحساب:

يتم التمييز في علم الإحصاء بين متوسط المجتمع (Population Mean) ومتوسط العينة (Sample Mean).

1. متوسط المجتمع (μ): يُستخدم عندما تكون لدينا بيانات لجميع أفراد المجتمع الإحصائي محل الدراسة. صيغته هي:
   μ = (Σ xᵢ) / N
   حيث:
   • μ (تقرأ “ميو”) هو رمز متوسط المجتمع.
   • Σ (سيجما) هو رمز المجموع.
   • xᵢ هي كل قيمة فردية في المجتمع.
   • N هو الحجم الكلي للمجتمع.
2. متوسط العينة (x̄): يُستخدم عندما نعمل على عينة مسحوبة من مجتمع أكبر، وهو الحال في معظم الأبحاث العملية. صيغته هي:
   x̄ = (Σ xᵢ) / n
   حيث:
   • x̄ (تقرأ “إكس بار”) هو رمز متوسط العينة.
   • xᵢ هي كل قيمة فردية في العينة.
   • n هو حجم العينة.

مثال تطبيقي: لنفترض أن لدينا درجات 9 طلاب في اختبار ما: {85, 90, 78, 92, 65, 88, 85, 95, 70}.
لحساب المتوسط الحسابي:
المجموع = 85 + 90 + 78 + 92 + 65 + 88 + 85 + 95 + 70 = 748
عدد القيم (n) = 9
المتوسط (x̄) = 748 / 9 ≈ 83.11

نقاط القوة والخصائص:

1. يأخذ كل قيمة في الاعتبار: الميزة الرئيسية للمتوسط الحسابي هي أنه يستخدم كل معلومة متاحة في مجموعة البيانات. كل قيمة، بغض النظر عن حجمها، تساهم في النتيجة النهائية.
2. التفرد: لكل مجموعة من البيانات الرقمية متوسط حسابي واحد فقط.
3. القابلية للمعالجة الجبرية: المتوسط الحسابي هو مقياس مستقر وله خصائص رياضية قوية تجعله أساساً للعديد من الأساليب الإحصائية المتقدمة، مثل تحليل التباين (ANOVA)، واختبارات (t-test)، والانحدار الخطي. لا يمكن بناء هذه النماذج باستخدام الوسيط أو المنوال بنفس السهولة.

نقاط الضعف والقيود (الحساسية للقيم المتطرفة):

إن أكبر نقطة ضعف للمتوسط الحسابي هي حساسيته الشديدة للقيم المتطرفة (Outliers)، وهي القيم التي تقع بعيداً جداً عن بقية البيانات. يمكن لقيمة متطرفة واحدة، سواء كانت كبيرة جداً أو صغيرة جداً، أن تسحب المتوسط بشكل كبير في اتجاهها، مما يعطي صورة مضللة عن “مركز” البيانات.

مثال توضيحي: لنأخذ المثال السابق لرواتب الموظفين في قسم صغير: {5000, 5200, 5500, 5800, 6000}.
المتوسط الحسابي = (5000 + 5200 + 5500 + 5800 + 6000) / 5 = 5500.
هنا، المتوسط يمثل البيانات بشكل جيد.

الآن، لنفترض أن مدير القسم، الذي يتقاضى راتباً قدره 40,000، انضم إلى مجموعة البيانات: {5000, 5200, 5500, 5800, 6000, 40000}.
المجموع الجديد = 67500
عدد القيم = 6
المتوسط الجديد = 67500 / 6 = 11,250.

هل المتوسط الجديد (11,250) يمثل راتب الموظف “النموذجي” في هذا القسم؟ بالطبع لا. خمسة من أصل ستة موظفين يتقاضون رواتب أقل بكثير من هذا الرقم. القيمة المتطرفة (40,000) سحبت المتوسط نحو الأعلى بشكل كبير، مما جعله مقياساً مضللاً في هذا السياق. هذا هو السبب في أننا نرى تقارير الدخل القومي غالباً ما تستخدم “الوسيط” بدلاً من “المتوسط”.

أنواع أخرى من المتوسطات:

من المهم أكاديمياً الإشارة إلى أن المتوسط الحسابي ليس النوع الوحيد من المتوسطات. هناك أنواع أخرى تُستخدم في سياقات محددة:

• المتوسط الهندسي (Geometric Mean): يُستخدم للبيانات التي تمثل نسب نمو أو معدلات مركبة، مثل عوائد الاستثمار. يتم حسابه عن طريق ضرب جميع القيم ثم أخذ الجذر النوني (حيث n هو عدد القيم). إنه يخفف من تأثير القيم الكبيرة جداً.
• المتوسط التوافقي (Harmonic Mean): يُستخدم عند حساب متوسط المعدلات أو النسب، مثل متوسط السرعة لرحلة مقسمة إلى أجزاء بسرعات مختلفة. صيغته هي مقلوب المتوسط الحسابي لمقالب القيم. إنه يعطي وزناً أكبر للقيم الأصغر.

H2: الوسيط (The Median): القيمة الصامدة في المنتصف

إذا كان المتوسط الحسابي هو مركز ثقل البيانات، فإن الوسيط هو نقطة المنتصف الجغرافية للبيانات. يُعرّف الوسيط بأنه القيمة التي تقع في منتصف مجموعة البيانات بعد ترتيبها تصاعدياً أو تنازلياً. إنه يقسم البيانات إلى نصفين متساويين تماماً: 50% من القيم أقل من أو تساوي الوسيط، و50% من القيم أكبر من أو تساوي الوسيط.

طريقة الحساب:

تختلف طريقة حساب الوسيط قليلاً اعتماداً على ما إذا كان عدد نقاط البيانات فردياً أم زوجياً.

1. إذا كان عدد القيم فردياً (n is odd):
   • أولاً، رتّب البيانات من الأصغر إلى الأكبر.الوسيط هو القيمة الموجودة في الموقع الأوسط بالضبط. يمكن إيجاد موقعها باستخدام الصيغة: (n + 1) / 2.
   مثال: لنستخدم مجموعة درجات الطلاب مرة أخرى: {65, 70, 78, 85, 85, 88, 90, 92, 95}. (تم ترتيبها).
   عدد القيم n = 9 (فردي).
   موقع الوسيط = (9 + 1) / 2 = 5.
   القيمة في الموقع الخامس هي 85. إذن، الوسيط هو 85.
2. إذا كان عدد القيم زوجياً (n is even):
   • أولاً، رتّب البيانات من الأصغر إلى الأكبر.
   • في هذه الحالة، لا توجد قيمة واحدة في المنتصف، بل قيمتان.
   • الوسيط هو المتوسط الحسابي للقيمتين الموجودتين في المنتصف. يمكن إيجاد موقعيهما باستخدام الصيغتين: n / 2 و (n / 2) + 1.
   مثال: لنضف درجة طالب آخر إلى المجموعة لتصبح: {65, 70, 78, 85, 85, 88, 90, 92, 95, 98}.
   عدد القيم n = 10 (زوجي).
   موقعا القيمتين في المنتصف هما: 10 / 2 = 5، و (10 / 2) + 1 = 6.
   القيمة في الموقع الخامس هي 85، والقيمة في الموقع السادس هي 88.
   الوسيط = (85 + 88) / 2 = 86.5.

نقاط القوة والخصائص (الصلابة ضد القيم المتطرفة):

الميزة الأبرز للوسيط هي صلابته أو مقاومته للقيم المتطرفة (Robustness to Outliers). على عكس المتوسط، لا يتأثر الوسيط بالقيم الشاذة في أطراف التوزيع.
لنعد إلى مثال رواتب الموظفين مع المدير: {5000, 5200, 5500, 5800, 6000, 40000}.
لنحسب الوسيط:

1. نرتب البيانات: {5000, 5200, 5500, 5800, 6000, 40000}.
2. n = 6 (زوجي). القيمتان في المنتصف هما في الموقع الثالث والرابع.
3. القيمتان هما 5500 و 5800.
4. الوسيط = (5500 + 5800) / 2 = 5650.

لاحظ الفرق الهائل: المتوسط كان 11,250، بينما الوسيط هو 5650. من الواضح أن الوسيط (5650) يقدم وصفاً أكثر واقعية وصدقاً للراتب “النموذجي” في هذا القسم، لأنه لم يتأثر براتب المدير المرتفع جداً. لهذا السبب، يُفضل استخدام الوسيط عند وصف البيانات التي يُحتمل أن تكون ملتوية (skewed) أو تحتوي على قيم متطرفة، مثل بيانات الدخل، أسعار المنازل، أو أوقات الاستجابة في التجارب.

نقاط الضعف والقيود:

1. يتجاهل معظم قيم البيانات: بينما يستخدم المتوسط كل قيمة، يعتمد الوسيط فقط على قيمة واحدة (أو اثنتين) في المنتصف. التغييرات في القيم القصوى (طالما أنها لا تتجاوز الوسيط) ليس لها أي تأثير على قيمته. قد يعتبر هذا إهداراً للمعلومات في بعض السياقات.
2. أقل قابلية للمعالجة الجبرية: الوسيط ليس له خصائص رياضية قوية مثل المتوسط. من الصعب استخدامه في الاختبارات الإحصائية المتقدمة. على سبيل المثال، وسيط مجموعة من العينات لا يساوي بالضرورة وسيط مجموع هذه العينات، على عكس المتوسط.
3. قد يكون أقل استقراراً في العينات الصغيرة: في العينات الصغيرة، يمكن أن يتغير الوسيط بشكل كبير بإضافة أو إزالة نقطة بيانات واحدة بالقرب من المركز.

H2: المنوال (The Mode): القيمة الأكثر شيوعاً

المنوال هو أبسط مقاييس النزعة المركزية من حيث المفهوم. يُعرّف المنوال بأنه القيمة الأكثر تكراراً أو شيوعاً في مجموعة البيانات. ببساطة، هو القيمة التي تظهر أكثر من أي قيمة أخرى.

طريقة الحساب:

لحساب المنوال، كل ما عليك فعله هو عد تكرار كل قيمة في مجموعة البيانات. القيمة التي تحصل على أعلى عدد من التكرارات هي المنوال.
مثال: في مجموعة درجات الطلاب {85, 90, 78, 92, 65, 88, 85, 95, 70}.
نلاحظ أن القيمة 85 تظهر مرتين، بينما تظهر كل القيم الأخرى مرة واحدة فقط. لذلك، المنوال هو 85.

خصائص وتوزيعات المنوال:

على عكس المتوسط والوسيط، يمكن لمجموعة البيانات أن تحتوي على:

• منوال واحد (Unimodal): مثل المثال أعلاه، حيث توجد قيمة واحدة هي الأكثر تكراراً.
• أكثر من منوال (Multimodal): إذا كانت هناك قيمتان لهما نفس التكرار الأعلى، تسمى البيانات “ثنائية المنوال” (Bimodal). إذا كانت هناك ثلاث قيم، تكون “ثلاثية المنوال” (Trimodal)، وهكذا.
  • مثال: في المجموعة {4, 5, 6, 6, 7, 8, 8, 9}، كل من 6 و 8 يظهران مرتين. لذلك، هذه المجموعة ثنائية المنوال، والمنوالان هما 6 و 8.
• لا يوجد منوال (No Mode): إذا ظهرت كل قيمة في مجموعة البيانات بنفس عدد المرات (عادة مرة واحدة)، فإنه لا يوجد منوال.
  • مثال: في المجموعة {10, 20, 30, 40, 50}، لا يوجد منوال.

نقاط القوة والخصائص:

1. سهولة الفهم والحساب: المنوال هو المقياس الأكثر بديهية. حتى غير المتخصصين يمكنهم فهم فكرة “الخيار الأكثر شعبية”.
2. المقياس الوحيد للبيانات الاسمية: هذه هي أهم ميزة للمنوال. المتوسط والوسيط يتطلبان بيانات رقمية يمكن ترتيبها وجمعها. أما المنوال، فيمكن استخدامه مع البيانات الفئوية أو الاسمية (Categorical/Nominal Data)، وهي البيانات التي تصف فئات غير مرتبة.
   • مثال: إذا سألنا 100 شخص عن لون سيارتهم المفضل، وكانت النتائج: {أبيض: 40, أسود: 30, فضي: 20, أحمر: 10}، فلا يمكننا حساب متوسط أو وسيط لهذه الألوان. لكن يمكننا بسهولة تحديد المنوال، وهو “أبيض”، لأنه اللون الأكثر تكراراً. هذا يجعله أداة حيوية في أبحاث السوق والمسوحات الاجتماعية.
3. لا يتأثر بالقيم المتطرفة: مثل الوسيط، المنوال لا يتأثر على الإطلاق بالقيم المتطرفة، لأنه يهتم فقط بالتكرار وليس بقيمة البيانات.

نقاط الضعف والقيود:

1. ليس بالضرورة أن يكون “مركزياً”: قد يقع المنوال في أي مكان في التوزيع، وقد لا يكون ممثلاً جيداً لمركز البيانات على الإطلاق، خاصة في التوزيعات غير المنتظمة أو متعددة الأنماط.
2. عدم الاستقرار: يمكن أن يتغير المنوال بشكل كبير مع تغييرات طفيفة في البيانات، خاصة في العينات الصغيرة. إضافة أو إزالة بضع نقاط بيانات يمكن أن يغير المنوال تماماً أو يجعله يختفي.
3. قد لا يكون موجوداً أو فريداً: كما ذكرنا، قد لا يكون للبيانات منوال، أو قد يكون لها أكثر من منوال، مما يقلل من فائدته كمقياس تلخيصي واحد.
4. ضعف الخصائص الرياضية: مثل الوسيط، المنوال ليس له خصائص جبرية قوية، مما يحد من استخدامه في التحليلات الإحصائية الأكثر تعقيداً.

H2: المقارنة الشاملة: متى نستخدم كل مقياس؟

إن اختيار المقياس الأنسب للنزعة المركزية ليس قراراً عشوائياً، بل يعتمد على عاملين حاسمين: نوع البيانات وشكل توزيع البيانات.

1. تأثير نوع البيانات (Levels of Measurement):

• البيانات الاسمية (Nominal): بيانات فئوية لا يمكن ترتيبها (مثل: الجنس، فصيلة الدم، الجنسية).
  • المقياس المناسب: المنوال فقط. لا يمكن حساب متوسط أو وسيط للألوان أو الأسماء.
• البيانات الترتيبية (Ordinal): بيانات فئوية يمكن ترتيبها، ولكن المسافات بين الفئات غير متساوية أو غير معروفة (مثل: مستويات الرضا “غير راضٍ، محايد، راضٍ”، الرتب العسكرية، مستويات التعليم).
  • المقاييس المناسبة: الوسيط والمنوال. الوسيط هو الأفضل هنا لأنه يحترم الترتيب (يمكننا إيجاد الفئة الوسطى). يمكن استخدام المنوال لإيجاد الفئة الأكثر شيوعاً. لا ينبغي استخدام المتوسط لأن العمليات الحسابية عليه تفترض مسافات متساوية بين القيم، وهذا غير صحيح في البيانات الترتيبية.
• البيانات الفاصلة والنسبية (Interval and Ratio): بيانات رقمية ذات مسافات متساوية بين القيم (مثل: درجة الحرارة، الطول، الوزن، الدخل). البيانات النسبية لها صفر حقيقي (مثل الوزن)، بينما البيانات الفاصلة ليس لها (مثل درجة الحرارة المئوية).
  • المقاييس المناسبة: المتوسط، الوسيط، والمنوال. هنا، يعتمد الاختيار بشكل أساسي على شكل التوزيع.

2. تأثير شكل توزيع البيانات (Shape of the Distribution):

شكل التوزيع، الذي يمكن تصوره باستخدام المدرج التكراري (Histogram)، له تأثير عميق على العلاقة بين المتوسط والوسيط والمنوال.

• التوزيع المتماثل (Symmetrical Distribution):
  في التوزيع المتماثل تماماً، مثل التوزيع الطبيعي (Normal Distribution)، يكون شكل البيانات متطابقاً على جانبي المركز. في هذه الحالة المثالية:
  المتوسط = الوسيط = المنوال
  تقع جميع المقاييس الثلاثة في نفس النقطة في قمة التوزيع. عندما تكون البيانات متماثلة تقريباً ولا تحتوي على قيم متطرفة، يُعتبر المتوسط هو أفضل مقياس للنزعة المركزية لأنه يستخدم كل البيانات المتاحة وهو قوي من الناحية الرياضية.
• التوزيع الملتوي إيجابياً (Positively Skewed Distribution):
  يُعرف أيضاً بالالتواء إلى اليمين (Skewed to the right). في هذا التوزيع، يكون لدى غالبية البيانات قيم منخفضة، مع وجود “ذيل” طويل من القيم المرتفعة القليلة (القيم المتطرفة) على الجانب الأيمن. مثال نموذجي هو توزيع الدخل.
  في هذه الحالة، العلاقة بين المقاييس هي:
  المتوسط > الوسيط > المنوال
  • المنوال: سيكون عند أعلى قمة في التوزيع (حيث تتركز معظم القيم المنخفضة).
  • الوسيط: سيكون إلى يمين المنوال، لأنه نقطة المنتصف العددية.
  • المتوسط: سيتم “سحبه” بعيداً نحو اليمين بفعل القيم المتطرفة المرتفعة، مما يجعله أعلى قيمة بين الثلاثة.
    في التوزيعات الملتوية إيجابياً، يُعتبر الوسيط أفضل مقياس للنزعة المركزية لأنه يقاوم تأثير القيم المتطرفة ويعطي صورة أكثر دقة عن القيمة “النموذجية”.
• التوزيع الملتوي سلبياً (Negatively Skewed Distribution):
  يُعرف أيضاً بالالتواء إلى اليسار (Skewed to the left). في هذا التوزيع، يكون لدى غالبية البيانات قيم مرتفعة، مع وجود “ذيل” طويل من القيم المنخفضة القليلة (القيم المتطرفة) على الجانب الأيسر. مثال على ذلك هو درجات الطلاب في اختبار سهل جداً (معظمهم حصل على درجات عالية، وقليل منهم حصل على درجات منخفضة جداً).
  في هذه الحالة، العلاقة بين المقاييس هي:
  المتوسط < الوسيط < المنوال
  • المنوال: سيكون عند أعلى قمة في التوزيع (حيث تتركز معظم القيم المرتفعة).
  • الوسيط: سيكون إلى يسار المنوال.
  • المتوسط: سيتم “سحبه” بعيداً نحو اليسار بفعل القيم المتطرفة المنخفضة، مما يجعله أقل قيمة بين الثلاثة.
    مرة أخرى، في التوزيعات الملتوية سلبياً، يُعتبر الوسيط بشكل عام المقياس الأكثر تمثيلاً للبيانات.

H2: ما بعد المقاييس المركزية: نظرة على أهمية مقاييس التشتت

إن فهم مقاييس النزعة المركزية خطوة أولى حاسمة، لكنها لا تروي القصة الكاملة. معرفة “مركز” البيانات لا يخبرنا شيئاً عن مدى انتشار أو تشتت هذه البيانات حول المركز. لنأخذ مجموعتي بيانات:

• المجموعة أ: {50, 50, 50, 50, 50}
• المجموعة ب: {10, 30, 50, 70, 90}

لكلا المجموعتين نفس المتوسط (50) ونفس الوسيط (50). ولكن من الواضح أنهما مختلفتان تماماً. المجموعة (أ) ليس بها أي تباين، بينما المجموعة (ب) بياناتها متشتتة على نطاق واسع.

وهنا يأتي دور “مقاييس التشتت” (Measures of Dispersion/Variability)، التي تصف مدى انتشار البيانات. من المهم دائماً الإبلاغ عن مقياس للنزعة المركزية إلى جانب مقياس للتشتت للحصول على صورة كاملة. المقاييس الرئيسية للتشتت هي:

1. المدى (Range): الفرق بين أعلى قيمة وأدنى قيمة. إنه بسيط ولكنه حساس جداً للقيم المتطرفة.
2. المدى الربيعي (Interquartile Range – IQR): الفرق بين الربيع الثالث (Q3 – القيمة التي تفصل أعلى 25% من البيانات) والربيع الأول (Q1 – القيمة التي تفصل أدنى 25% من البيانات). IQR يمثل مدى الـ 50% الوسطى من البيانات، وهو مقياس تشتت صلب (robust) لأنه لا يتأثر بالقيم المتطرفة. غالباً ما يتم إقرانه بالوسيط.
3. التباين (Variance) والانحراف المعياري (Standard Deviation): هما أكثر مقاييس التشتت شيوعاً. يقيس الانحراف المعياري (الجذر التربيعي للتباين) متوسط بعد كل نقطة بيانات عن المتوسط الحسابي. الانحراف المعياري الكبير يعني أن البيانات متشتتة على نطاق واسع، بينما الانحراف المعياري الصغير يعني أن البيانات متجمعة بإحكام حول المتوسط. يتم إقران الانحراف المعياري دائماً بالمتوسط الحسابي.

H2: الخاتمة: قوة السياق والتكامل في التحليل الإحصائي

إن المتوسط الحسابي، الوسيط، والمنوال ليست مجرد مفاهيم رياضية مجردة، بل هي عدسات مختلفة ننظر من خلالها إلى بياناتنا، وكل عدسة تكشف عن جانب مختلف من الحقيقة. المتوسط يوفر لنا مركز الثقل الرياضي، وهو أداة قوية عندما تكون البيانات متماثلة. الوسيط يوفر لنا النقطة الوسطى الحقيقية، وهو حارس أمين ضد تشويه القيم المتطرفة في البيانات الملتوية. أما المنوال، فيكشف لنا عن النمط الأكثر شيوعاً، وهو بطل البيانات الفئوية الذي لا غنى عنه.

لا يوجد مقياس “أفضل” بشكل مطلق. المقياس الأفضل هو الذي يتناسب مع سؤال البحث، ونوع البيانات، وطبيعة توزيعها. المحلل الإحصائي الماهر لا يحفظ التعريفات فحسب، بل يفهم الفروق الدقيقة بين هذه المقاييس ويعرف متى يثق في كل منها. في كثير من الأحيان، تكمن القوة الحقيقية في استخدامها معاً. إن مقارنة المتوسط بالوسيط هي في حد ذاتها أداة تشخيصية قوية تكشف عن وجود التواء في البيانات. إن الإبلاغ عن المتوسط مع الانحراف المعياري، أو الوسيط مع المدى الربيعي، يقدم قصة أكثر ثراءً واكتمالاً من أي رقم واحد بمفرده.

في النهاية، تمثل هذه المقاييس الثلاثة البسيطة حجر الأساس الذي تُبنى عليه صروح التحليل الإحصائي الشاهقة. إن إتقانها ليس مجرد خطوة أولى، بل هو بوصلة دائمة توجهنا نحو فهم أعمق وأكثر دقة للغة الأرقام التي تشكل عالمنا.