قانون كولوم: كيف يفسر التفاعل بين الشحنات الكهربائية؟
ما هي العلاقة الرياضية التي تحكم القوى الكهروستاتيكية؟
يمثل فهم القوى الكهربائية بين الجسيمات المشحونة أحد الأسس الجوهرية في علم الفيزياء الحديثة. لقد ساهم هذا الفهم في تطوير العديد من التقنيات التي نستخدمها يومياً، من الأجهزة الإلكترونية إلى أنظمة الاتصالات اللاسلكية.
ما هو قانون كولوم وما أهميته في الفيزياء؟
يُعَدُّ قانون كولوم واحداً من القوانين الأساسية في الكهرومغناطيسية؛ إذ يصف بدقة كيفية تفاعل الشحنات الكهربائية مع بعضها البعض. ينص هذا القانون على أن القوة الكهروستاتيكية (Electrostatic Force) بين شحنتين نقطيتين تتناسب طردياً مع حاصل ضرب مقداري الشحنتين، وعكسياً مع مربع المسافة بينهما. فما هي الأهمية الحقيقية لهذا القانون؟ الإجابة تكمن في أنه يوفر أساساً رياضياً دقيقاً لفهم كيفية ترابط الذرات وتشكيل الجزيئات والمواد.
بالإضافة إلى ذلك، فإن قانون كولوم يشكل حجر الزاوية في فهم الكهرباء الساكنة والمجالات الكهربائية. إن التطبيقات العملية لهذا القانون تمتد من المستوى الذري الدقيق وصولاً إلى الأنظمة الصناعية الكبرى؛ إذ يستخدم في تصميم المكثفات الكهربائية، وفي تفسير كيفية عمل الطابعات الليزرية، وحتى في فهم سلوك البروتينات داخل الخلايا الحية. كما أن هذا القانون يساعدنا في تفسير العديد من الظواهر اليومية مثل التصاق الملابس ببعضها بعد إخراجها من النشافة أو انجذاب الشعر نحو مشط بلاستيكي.
من هو تشارلز كولوم ومتى اكتشف هذا القانون؟
كان الفيزيائي الفرنسي شارل أوغستان دو كولوم (Charles-Augustin de Coulomb) رائداً في مجال الكهرومغناطيسية خلال القرن الثامن عشر. ولد كولوم في عام 1736 في مدينة أنغوليم الفرنسية، وكرّس حياته لدراسة القوى الفيزيائية المختلفة. لقد عمل كولوم كمهندس عسكري قبل أن يتفرغ للبحث العلمي، وهذه الخلفية الهندسية ساعدته كثيراً في تصميم الأدوات التجريبية الدقيقة.
في عام 1785، نشر كولوم سلسلة من الأوراق البحثية التي وصف فيها تجاربه المبتكرة باستخدام ميزان الالتواء (Torsion Balance)؛ إذ صمم هذا الجهاز الحساس ليقيس القوى الضعيفة جداً بين الشحنات الكهربائية. من جهة ثانية، فقد استخدم نفس المبدأ لقياس القوى المغناطيسية أيضاً. وبالتالي، فإن ميزان الالتواء الذي طوره كان ثورياً في زمنه، مشابهاً لما فعله هنري كافنديش لاحقاً في قياس قوة الجاذبية الأرضية. الجدير بالذكر أن دقة قياسات كولوم كانت مذهلة بالنسبة لتلك الحقبة، وأسست لمنهجية علمية صارمة في دراسة الكهرباء.
ما هي الصيغة الرياضية لقانون كولوم؟
الصيغة والمتغيرات
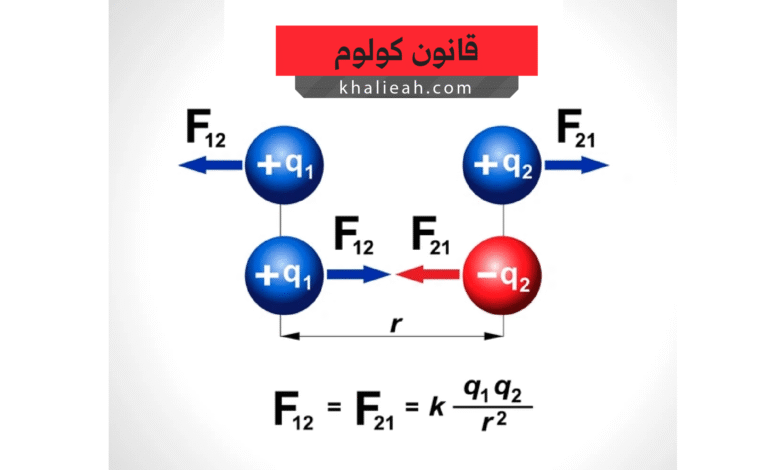
تُكتب الصيغة الرياضية لقانون كولوم على النحو التالي: F = k × (q₁ × q₂) / r². إن هذه المعادلة البسيطة في مظهرها تحمل معاني فيزيائية عميقة. دعونا نفصّل مكوناتها:
- F: مقدار القوة الكهروستاتيكية المؤثرة بين الشحنتين، وتُقاس بوحدة النيوتن
- k: ثابت كولوم (Coulomb’s Constant) ويساوي تقريباً 8.99 × 10⁹ نيوتن·متر²/كولوم²
- q₁ وq₂: مقدار الشحنتين الكهربائيتين الأولى والثانية، وتُقاسان بوحدة الكولوم
- r: المسافة الفاصلة بين مركزي الشحنتين، وتُقاس بوحدة المتر
من ناحية أخرى، يمكن كتابة ثابت كولوم بصيغة أخرى: k = 1 / (4πε₀)، حيث ε₀ هي سماحية الفراغ (Permittivity of Free Space) وتساوي 8.85 × 10⁻¹² فاراد/متر. وعليه فإن اختيار الصيغة يعتمد على السياق والتفضيل الشخصي، لكن كلتا الصيغتين تعطيان النتائج ذاتها. كما أن استخدام سماحية الفراغ يربط قانون كولوم بمعادلات ماكسويل الأعم والأشمل في الكهرومغناطيسية.
كيف تؤثر المسافة بين الشحنات على قوة التفاعل؟
إن العلاقة العكسية التربيعية بين القوة والمسافة تمثل جوهر قانون كولوم. فماذا يعني ذلك عملياً؟ يعني أنه عندما تضاعف المسافة بين شحنتين، فإن القوة بينهما تنخفض إلى الربع فقط. بينما إذا قللت المسافة إلى النصف، فإن القوة تتضاعف أربع مرات. هذه العلاقة الرياضية ليست عشوائية؛ إذ تعكس الطبيعة الهندسية ثلاثية الأبعاد للفضاء الذي نعيش فيه.
انظر إلى مثال عملي: لو كانت لديك شحنتان متماثلتان على بعد 1 متر، وكانت القوة بينهما 9 نيوتن. إذاً كيف تتغير القوة عند المسافات المختلفة؟ عند مسافة 2 متر، تصبح القوة 2.25 نيوتن (أي 9÷4). وعند مسافة 3 أمتار، تصبح القوة 1 نيوتن فقط (أي 9÷9). بالمقابل، عند تقريب الشحنتين إلى 0.5 متر، تصبح القوة 36 نيوتن (أي 9×4). هذا السلوك الرياضي يفسر لماذا تكون القوى الكهربائية داخل الذرة قوية جداً؛ إذ إن المسافات بين الإلكترونات والنواة صغيرة للغاية، مما يولد قوى هائلة نسبياً رغم صغر الشحنات.
ما الفرق بين قوى التجاذب والتنافر الكهروستاتيكية؟
يحدد قانون كولوم ليس فقط مقدار القوة بل أيضاً اتجاهها. فهل يا ترى الشحنات تتجاذب دائماً أم تتنافر؟ الجواب يعتمد على إشارة الشحنات. عندما تكون الشحنتان من النوع نفسه (موجبتان معاً أو سالبتان معاً)، فإنهما تتنافران؛ إذ تكون القوة دافعة تبعد إحداهما عن الأخرى. هذا التنافر هو السبب وراء عدم انهيار النواة الذرية رغم احتوائها على بروتونات موجبة متقاربة جداً – لكن القوة النووية القوية تتغلب على هذا التنافر.
على النقيض من ذلك، عندما تكون الشحنتان مختلفتين (إحداهما موجبة والأخرى سالبة)، فإنهما تتجاذبان بقوة. إن هذا التجاذب مسؤول عن الترابط بين الإلكترونات والنواة في الذرة، وكذلك عن تشكيل الروابط الأيونية بين العناصر المختلفة. لقد أثبتت التجارب المخبرية هذه الحقائق مراراً وتكراراً منذ زمن كولوم وحتى اليوم. فقد كان بنجامين فرانكلين قد اقترح مسبقاً وجود نوعين من الكهرباء، لكن كولوم هو من وضع الإطار الكمي الدقيق لهذه الملاحظات.
ما هي التطبيقات العملية لقانون كولوم؟
تطبيقات متنوعة في حياتنا اليومية
يدخل قانون كولوم في عدد كبير من التطبيقات التقنية والعلمية:
- الطابعات الليزرية والنسخ: تستخدم مبدأ جذب جزيئات الحبر المشحونة إلى الأماكن المشحونة بشحنة معاكسة على الأسطوانة الضوئية
- أنظمة تنقية الهواء: تعمل المرشحات الإلكتروستاتيكية على شحن الجسيمات الملوثة ثم جمعها باستخدام الألواح المشحونة
- مسرعات الجسيمات: تستخدم القوى الكهروستاتيكية لتسريع البروتونات والإلكترونات إلى سرعات هائلة
- شاشات اللمس السعوية: تعتمد على اكتشاف التغيرات في المجال الكهربائي عند اقتراب الإصبع المشحون
- طلاء السيارات بالرش الكهروستاتيكي: يضمن توزيعاً متساوياً للطلاء عبر شحن قطرات الطلاء وسطح السيارة بشحنات معاكسة
- أجهزة إزالة الغبار الإلكتروستاتيكية: المستخدمة في الصناعات الدقيقة والغرف النظيفة
بالإضافة إلى ذلك، فإن فهم قانون كولوم ضروري في الكيمياء الحيوية لتفسير كيفية طي البروتينات وتفاعل الجزيئات الحيوية. ومما يثير الاهتمام أن العديد من الأدوية تعمل عبر تفاعلات كهروستاتيكية مع مواقع محددة في الجسم. وكذلك في علم المواد، يساعد هذا القانون في تصميم مواد جديدة ذات خصائص كهربائية محددة، من أشباه الموصلات إلى العوازل الفائقة.
كيف يرتبط قانون كولوم بالمجال الكهربائي؟
يمكن إعادة صياغة قانون كولوم باستخدام مفهوم المجال الكهربائي (Electric Field)، وهو مفهوم أكثر عمومية وشمولية. برأيكم ماذا يمثل المجال الكهربائي؟ الإجابة هي أنه يمثل التأثير الذي تحدثه شحنة كهربائية في الفضاء المحيط بها. إن المجال الكهربائي عند نقطة معينة يُعرّف بأنه القوة التي تؤثر على وحدة الشحنة الموضوعة عند تلك النقطة، ويُحسب بالعلاقة: E = k × q / r².
من جهة ثانية، فإن استخدام مفهوم المجال الكهربائي يسهّل التعامل مع الأنظمة المعقدة التي تحتوي على شحنات متعددة. بدلاً من حساب القوة بين كل زوج من الشحنات، يمكننا حساب المجال الكهربائي الناتج عن جميع الشحنات ثم ضربه في مقدار أي شحنة اختبار لمعرفة القوة عليها. وبالتالي، فإن مبدأ التراكب (Principle of Superposition) ينطبق هنا؛ إذ إن المجال الكهربائي الكلي عند نقطة ما يساوي مجموع المجالات الناتجة عن كل شحنة على حدة.
ما هي حدود وقيود قانون كولوم؟
رغم دقته الكبيرة، فإن قانون كولوم له حدود معينة يجب إدراكها. أولاً، ينطبق القانون بدقة فقط على الشحنات النقطية أو الأجسام الكروية المشحونة بانتظام؛ إذ تتصرف الكرة المشحونة بانتظام وكأن كامل شحنتها مركزة في مركزها عند النظر إليها من الخارج. لكن في حالة الأجسام ذات الأشكال المعقدة أو التوزيعات الشحنية غير المنتظمة، يتطلب الأمر استخدام التكامل الرياضي لحساب القوة الكلية.
ثانياً، يفترض قانون كولوم أن الشحنات ثابتة أو تتحرك ببطء شديد. هل سمعت بالإشعاع الكهرومغناطيسي؟ عندما تتسارع الشحنات الكهربائية، فإنها تشع طاقة على شكل موجات كهرومغناطيسية، وهذا لا يؤخذ في الحسبان في الصيغة البسيطة لقانون كولوم. كما أن القانون يفترض أن الوسط المحيط بالشحنات هو الفراغ أو الهواء. في الأوساط الأخرى مثل الماء أو الزيت، يجب تعديل ثابت كولوم بقسمته على الثابت العازلي (Dielectric Constant) للوسط، والذي يقلل القوة الفعالة بين الشحنات بشكل ملحوظ – وهذا ما يفسر لماذا تذوب الأملاح الأيونية في الماء بسهولة.
الخاتمة
لقد شكّل قانون كولوم نقطة تحول محورية في فهمنا للكهرباء والمغناطيسية، ووضع أساساً متيناً للفيزياء الكلاسيكية. إن هذا القانون ليس مجرد معادلة رياضية؛ بل هو نافذة نطل منها على عالم التفاعلات الأساسية بين المادة. من الذرة الصغيرة إلى المكثفات الضخمة في محطات الطاقة، يظل قانون كولوم أداة لا غنى عنها للفيزيائيين والمهندسين على حد سواء.
فقد ساهم هذا القانون في تطوير نظرية الكهرومغناطيسية الشاملة التي صاغها جيمس كلارك ماكسويل لاحقاً، والتي توحّد الكهرباء والمغناطيسية في إطار واحد. وكذلك مهّد الطريق لفهم البنية الذرية والكيمياء الكمية في القرن العشرين. إن دراسة قانون كولوم تمنح الطالب المبتدئ رؤية واضحة لكيفية عمل الطبيعة وفق قوانين رياضية دقيقة يمكن اختبارها وقياسها.
هل تساءلت يوماً كيف يمكنك تطبيق فهمك لقانون كولوم في تفسير الظواهر الكهربائية من حولك أو في تطوير مشاريع علمية مبتكرة؟
خمسة تمارين مناسبة لكل المستويات
التمرين الأول
شحنتان كهربائيتان q₁ = 3 × 10⁻⁶ C و q₂ = 4 × 10⁻⁶ C موضوعتان على بعد r = 0.2 m من بعضهما في الفراغ. احسب القوة الكهروستاتيكية بينهما.
الحل:
F = k × (q₁ × q₂) / r²
F = (9 × 10⁹) × (3 × 10⁻⁶ × 4 × 10⁻⁶) / (0.2)²
F = (9 × 10⁹) × (12 × 10⁻¹²) / 0.04
F = 108 × 10⁻³ / 0.04
F = 2.7 N
القوة الكهروستاتيكية بين الشحنتين تساوي 2.7 نيوتن وهي قوة تنافر لأن الشحنتين موجبتان.
التمرين الثاني
إذا كانت القوة بين شحنتين متساويتين على بعد 3 m تساوي 5 N، فما هي القوة بينهما إذا أصبحت المسافة 6 m؟
الحل:
بما أن القوة تتناسب عكسياً مع مربع المسافة:
F₁ / F₂ = (r₂)² / (r₁)²
5 / F₂ = (6)² / (3)²
5 / F₂ = 36 / 9 = 4
F₂ = 5 / 4 = 1.25 N
القوة الجديدة تساوي 1.25 نيوتن.
التمرين الثالث
شحنة q₁ = +8 × 10⁻⁹ C وشحنة q₂ = -2 × 10⁻⁹ C تفصل بينهما مسافة 0.5 m. احسب مقدار القوة وحدد نوعها.
الحل:
F = k × |q₁ × q₂| / r²
F = (9 × 10⁹) × (8 × 10⁻⁹ × 2 × 10⁻⁹) / (0.5)²
F = (9 × 10⁹) × (16 × 10⁻¹⁸) / 0.25
F = 144 × 10⁻⁹ / 0.25
F = 5.76 × 10⁻⁷ N
القوة تساوي 5.76 × 10⁻⁷ نيوتن وهي قوة تجاذب لأن الشحنتين مختلفتان.
التمرين الرابع
ثلاث شحنات موضوعة على خط مستقيم: q₁ = 5 μC عند الموضع x = 0، q₂ = -3 μC عند x = 0.3 m، q₃ = 4 μC عند x = 0.5 m. احسب القوة المحصلة على q₂.
الحل:
القوة من q₁ على q₂:
F₁₂ = (9 × 10⁹) × (5 × 10⁻⁶ × 3 × 10⁻⁶) / (0.3)²
F₁₂ = 1.5 N (باتجاه q₁ لأنها قوة تجاذب)
القوة من q₃ على q₂:
F₃₂ = (9 × 10⁹) × (4 × 10⁻⁶ × 3 × 10⁻⁶) / (0.2)²
F₃₂ = 2.7 N (باتجاه q₃ لأنها قوة تجاذب)
القوة المحصلة = F₃₂ – F₁₂ = 2.7 – 1.5 = 1.2 N باتجاه q₃.
التمرين الخامس
احسب المسافة بين شحنتين متساويتين q = 6 × 10⁻⁸ C إذا كانت قوة التنافر بينهما 1.8 × 10⁻³ N.
الحل:
F = k × q² / r²
r² = k × q² / F
r² = (9 × 10⁹) × (6 × 10⁻⁸)² / (1.8 × 10⁻³)
r² = (9 × 10⁹) × (36 × 10⁻¹⁶) / (1.8 × 10⁻³)
r² = 324 × 10⁻⁷ / 1.8 × 10⁻³ = 0.18
r = √0.18 = 0.424 m
المسافة بين الشحنتين تساوي 0.424 متر تقريباً.
خمسة تمارين لمستوى المدارس الثانوية
التمرين الأول (ثانوي)
شحنتان نقطيتان q₁ = 2 × 10⁻⁶ C و q₂ = -5 × 10⁻⁶ C على بعد 30 cm من بعضهما. احسب:
أ) القوة بينهما
ب) المجال الكهربائي عند نقطة منتصف المسافة بينهما
الحل:
أ) حساب القوة:
F = k × |q₁ × q₂| / r²
F = (9 × 10⁹) × (2 × 10⁻⁶ × 5 × 10⁻⁶) / (0.3)²
F = (9 × 10⁹) × (10 × 10⁻¹²) / 0.09
F = 1 N (قوة تجاذب)
ب) المجال عند المنتصف (r₁ = r₂ = 0.15 m):
E₁ = k × q₁ / (0.15)² = (9 × 10⁹) × (2 × 10⁻⁶) / 0.0225 = 8 × 10⁵ N/C (باتجاه q₁)
E₂ = k × q₂ / (0.15)² = (9 × 10⁹) × (5 × 10⁻⁶) / 0.0225 = 2 × 10⁶ N/C (باتجاه q₂)
المجال المحصل = E₁ + E₂ = 2.8 × 10⁶ N/C باتجاه الشحنة السالبة.
التمرين الثاني (ثانوي)
أربع شحنات متساوية Q موضوعة عند زوايا مربع طول ضلعه a = 0.4 m. إذا كانت القوة المحصلة على إحدى الشحنات 0.3 N، احسب قيمة Q.
الحل:
القوة من الشحنة المقابلة (قطر = a√2):
F_diagonal = k × Q² / (a√2)² = k × Q² / (2a²)
القوة من كل شحنة مجاورة:
F_adjacent = k × Q² / a²
القوة المحصلة من الشحنتين المجاورتين (زاوية 90°):
F_adj_total = √2 × (k × Q² / a²)
القوة الكلية:
F_total = F_diagonal + F_adj_total = k × Q² / (2a²) + √2 × (k × Q² / a²)
F_total = (k × Q² / a²) × (0.5 + 1.414) = 1.914 × k × Q² / a²
0.3 = 1.914 × (9 × 10⁹) × Q² / (0.16)
Q² = 0.3 × 0.16 / (1.914 × 9 × 10⁹) = 2.79 × 10⁻¹²
Q = 1.67 × 10⁻⁶ C = 1.67 μC
التمرين الثالث (ثانوي)
شحنة اختبار q₀ = 2 × 10⁻⁹ C موضوعة في مجال كهربائي منتظم E = 4 × 10⁴ N/C. احسب:
أ) القوة على الشحنة
ب) التسارع إذا كانت كتلة الشحنة m = 1 × 10⁻¹⁵ kg
ج) السرعة بعد قطع مسافة 5 cm من السكون
الحل:
أ) القوة:
F = q₀ × E = (2 × 10⁻⁹) × (4 × 10⁴) = 8 × 10⁻⁵ N
ب) التسارع:
a = F / m = (8 × 10⁻⁵) / (1 × 10⁻¹⁵) = 8 × 10¹⁰ m/s²
ج) السرعة:
v² = 2 × a × d
v² = 2 × (8 × 10¹⁰) × 0.05 = 8 × 10⁹
v = 8.94 × 10⁴ m/s
التمرين الرابع (ثانوي)
قطرة زيت كتلتها m = 1.6 × 10⁻¹⁴ kg ومشحونة بشحنة q معلقة في مجال كهربائي شاقولي موجه نحو الأسفل. إذا كان المجال E = 2 × 10⁴ N/C، احسب مقدار الشحنة وحدد إشارتها. (g = 10 m/s²)
الحل:
لكي تبقى القطرة معلقة، يجب أن تتساوى القوة الكهربائية مع وزن القطرة:
F_electric = Weight
q × E = m × g
q = (m × g) / E
q = (1.6 × 10⁻¹⁴ × 10) / (2 × 10⁴)
q = 8 × 10⁻¹⁸ C
الشحنة موجبة لأن المجال موجه نحو الأسفل والقوة الكهربائية يجب أن تكون نحو الأعلى لتوازن الوزن.
التمرين الخامس (ثانوي)
إلكترونان يفصل بينهما مسافة r = 1 × 10⁻¹⁰ m (تقريباً نصف قطر الذرة). احسب:
أ) قوة التنافر بينهما
ب) نسبة هذه القوة إلى وزن الإلكترون
علماً أن: شحنة الإلكترون e = 1.6 × 10⁻¹⁹ C، كتلة الإلكترون m_e = 9.1 × 10⁻³¹ kg
الحل:
أ) قوة التنافر:
F = k × e² / r²
F = (9 × 10⁹) × (1.6 × 10⁻¹⁹)² / (1 × 10⁻¹⁰)²
F = (9 × 10⁹) × (2.56 × 10⁻³⁸) / (1 × 10⁻²⁰)
F = 2.304 × 10⁻⁸ N
ب) النسبة إلى الوزن:
Weight = m_e × g = 9.1 × 10⁻³¹ × 10 = 9.1 × 10⁻³⁰ N
Ratio = F / Weight = (2.304 × 10⁻⁸) / (9.1 × 10⁻³⁰)
Ratio = 2.53 × 10²¹
القوة الكهروستاتيكية أكبر بحوالي 10²¹ مرة من وزن الإلكترون، مما يوضح أن القوى الكهربائية أقوى بكثير من الجاذبية على المستوى الذري.





